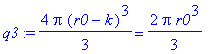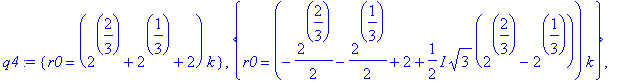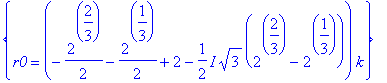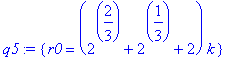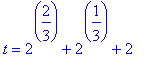Example 1
Problem
The volume of a spherical balloon is increasing at a rate of 400 cubic inches per minute. Find the instantaneous rate at which the radius is increasing when the radius is 8 inches.
REQUEST: customized maplet
This maplet, RRSphere (?), would provide an interface to creating animations of an inflating balloon. A slider could be used to select the rate at which air is being added - or removed - from the balloon. The initial size/volume would be needed. Each frame would need to report the time, radius, volume, and possibly surface area. (Or, the user could select which of these quantities should be reported in each frame.) To be slightly more general, it would be nice to allow the user to specify if the given rate is volume, surface area, or radius. Let me know if you need any more information than this.
| > |
Solution 1
Let the volume and radius of the spherical balloon be
![]() and
and
![]() , respectively, and let
, respectively, and let
![]() denote time (the independent variable in this problem). The problem tells us that
denote time (the independent variable in this problem). The problem tells us that
![]() = 400 cubic inches/min and
= 400 cubic inches/min and
![]() inches. The objective is to determine
inches. The objective is to determine
![]() when
when
![]() inches and
inches and
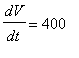 inches/min.
inches/min.
No relationship between
![]() and
and
![]() is provided in the problem. However, because the balloon is a sphere, we know
is provided in the problem. However, because the balloon is a sphere, we know
| > | q1 := V=4/3*Pi*r^3: q1; |
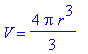
Implicit in the problem is the statement that both volume and radius are functions of time,
![]() . Thus, the relationship between
. Thus, the relationship between
![]() and
and
![]() is really:
is really:
| > | q2 := eval( q1, [V=V(t),r=r(t)] ): q2; |
![]()
Differentiation of this relationship with respect to
![]() yields (by the
Chain Rule):
yields (by the
Chain Rule):
| > | q3 := diff( q2, t ): q3; |
![]()
Now that all differentiation is complete it is permissible to insert the given values and solve for the unknown quantity. Here, the given information is
| > | d1 := [ diff(V(t),t)=400, r(t)=8 ]: d1; |
![]()
and it is simple to solve for the rate of change of the radius
| > | q4 := isolate( q3, diff(r(t),t) ): q4; |
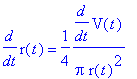
When this numeric data is substituted into the differentiated relationship
| > | q5 := lhs(q4) = eval( rhs(q4), d1 ): q5; ` ` = evalf(rhs(q5)); |
![]()
![]()
When the volume is increasing at 400 cubic inches per minute and the radius is 8 inches, the radius is increasing at a rate of 0.497 inches per minute.
| > |
- Enter the formula for the volume of a sphere, V=4/3*Pi*r^3 , in the Equation or Relationship field.
- In the Dependent Variable(s) field, enter V and r between the square brackets: [ V, r ]
- Time is the independent variable; in the Independent Variable field, enter t .
- There are no constants (parameters that do not change at all during the problem); do not change the Constants field: [ ]
- The information that the radius is 8 inches is specified by changing the Values of Variables field to [ r = 8 ]
-
The only given rate of change is
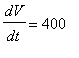 in
in
 /min; in the
Values of Rates of Change
field, enter
D(V) = 400
/min; in the
Values of Rates of Change
field, enter
D(V) = 400
Note the notation used to indicate a rate of change. This is a special notation that is understood only within the RelatedRates maplet. - The rate of change of the radius is the quantity that we seek to determine; the Quantity to be determined field should contain D(r)
Solution 2 -- RelatedRates Maplet
The solution of this problem can also be obtained using the RelatedRates maplet [ Maplet Viewer][ MapleNet].
| > |
Step 0
Launch the RelatedRates maplet using either the Maplet Viewer, if you have Maple 8 on your local computer, or via MapleNet, if you want to access Maple over the WWW.
| > |
Step 1
Enter all given information about the problem:
| > |
Step 2
To prepare to differentiate the volume formula, make the Equation or Relationship field active.
The active field should now be V = 4/3*Pi*r^3
| > |
Note: The ``Active Equation''
The maplet performs operations on the Active Equation/Relationship . To make the contents of a field ``active'', position the cursor over the field and click the right mouse button, select the second entry: Make Active .
| > |
Step 3
Differentiate the volume formula with respect to time by clicking the Diff wrt indep var button. The result of this differentiation is displayed using D(V) and D(r) to represent the rates of change of volume and radius, respectively. Conclude by making this result the active equation.
The active equation should now be D(V) = 4*Pi*r^2*D(r)
| > |
Step 4
To substitute the given values and rates into the differentiated relationship, click on the Subs variables button, make the result active, click on the Subs rates of change button, and make this result active. (The two substitutions can be done in either order.)
At the end of Step 4 the active equation should be 400 = 256*Pi*D(r)
| > |
Step 5
Solve for the unknown quantity by clicking on the Solve for unknown quantity button.
(To see a floating-point version of any result, click the right mouse button over a field, select the first menu option ( Manipulate ), and then evalf .)
The result should be D(r) = 25/16/Pi or D(r) = .4973591970
| > |
This completes the solution using the RelatedRates maplet. For this problem the maplet is not truly necessary. But, when there are more variables, a more complicated relationship, or other complicating features, the maplet can be a real timesaver.
| > |
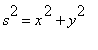 or
or
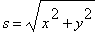
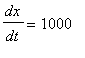 km/hr and
km/hr and
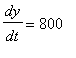 km/hr.
km/hr.
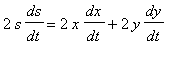 or
or
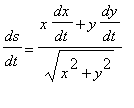
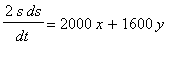 or
or
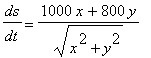
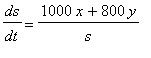
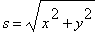 =
=
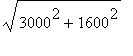 = 3400 km. Substituting these values in the formula for the rate of change of the distance yields:
= 3400 km. Substituting these values in the formula for the rate of change of the distance yields:
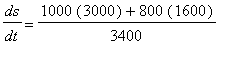 =
=
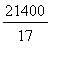 = 1258.824 km/hr.
= 1258.824 km/hr.
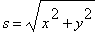 =
=
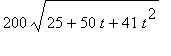 and
and
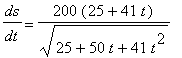
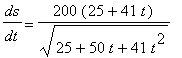
![[Maple Plot]](images/RelatedRates67.gif)
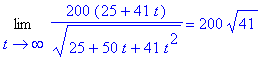
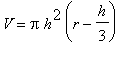 .
.

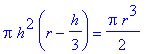



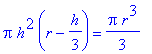
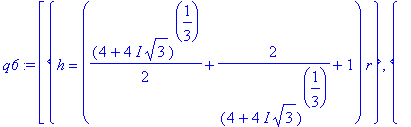
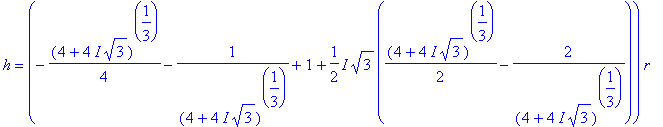
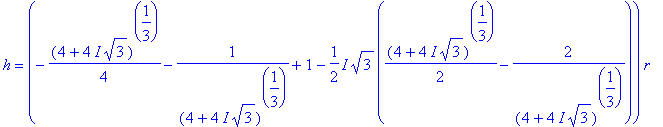
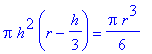
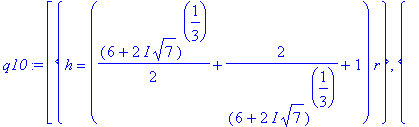
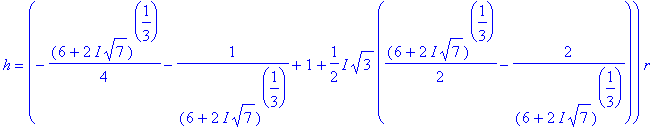
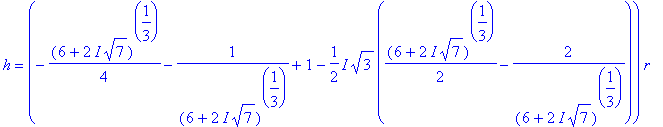
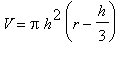
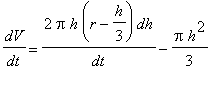
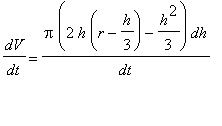 =
=
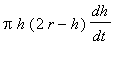
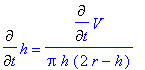
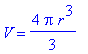
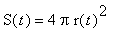 , in this formula. This allows us to rewrite the rate of change of the volume as
, in this formula. This allows us to rewrite the rate of change of the volume as
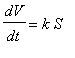 , for some constant
, for some constant
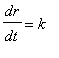 ,
,