Point 1: When Are Global Extrema Attained as Function Values?
A careful examination of the definitions of global extrema reveals that the extreme values are not required to be values of the function. In fact, if we define the maximum value to be
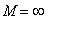 for a function that is not bounded above and the minimum value to be
for a function that is not bounded above and the minimum value to be
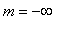 for a function that is not bounded below, then every function has global extrema. The more important question is:
for a function that is not bounded below, then every function has global extrema. The more important question is:
When are the global extrema attained as values of the function from the given domain?
Theorem: Global Max/Min Existence Theorem
Given a continuous function f on a closed and bounded interval,
![[a, b]](images/GlobalAnalysis20.gif) , there is a global maximum and a global minimum of f on
, there is a global maximum and a global minimum of f on
![[a, b]](images/GlobalAnalysis21.gif) .
.
One good way of understanding this theorem is to look at all the ways the hypotheses can fail to hold.
-
If the function is not continuous on the closed interval
![[a, b]](images/GlobalAnalysis22.gif) , then the function may or may not have global extrema.
, then the function may or may not have global extrema.
-
If the function is continuous but the interval is not closed, then the function may or may not have global extrema.
-
If the function is continuous but the interval is not bounded, then the function may or may not have global extrema.
Example 1: Discontinuous Function on Closed and Bounded Interval
Consider the function
| > |
f1 := piecewise( x< 1, x, x<2, (x-1)/2 );
|
![f1 := PIECEWISE([x, x < 1],[1/2*x-1/2, x < 2])](images/GlobalAnalysis23.gif)
on the closed and bounded interval
![[0, 2]](images/GlobalAnalysis24.gif) .
.
| > |
plot( f1, x=0..2, discont=true,
title="Discontinuous Function that does Not Attain Its Global Maximum on [0,2]" );
|
![[Maple Plot]](images/GlobalAnalysis25.gif)
This function is discontinuous at
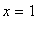 . The smallest number with the property that
. The smallest number with the property that
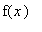 <=
<=
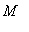 for all x in
for all x in
![[0, 2]](images/GlobalAnalysis29.gif) is
is
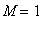 . Because there is no
. Because there is no
 in
in
![[0, 2]](images/GlobalAnalysis32.gif) with
with
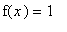 , this function
does
not
attain its global maximum on
, this function
does
not
attain its global maximum on
![[0, 2]](images/GlobalAnalysis34.gif) . Conversely, the largest number with the property that
. Conversely, the largest number with the property that
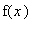 >=
>=
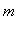 for all
for all
 in
in
![[0, 2]](images/GlobalAnalysis38.gif) is
is
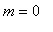 . Because
. Because
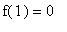 , this function
does attain its global minimum on
, this function
does attain its global minimum on
![[0, 2]](images/GlobalAnalysis41.gif) . (In fact, the global minimum is attained at both
. (In fact, the global minimum is attained at both
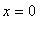 and
and
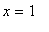 .)
.)
Note that it is important to clearly state the interval when talking about global extrema.
Example 2: Continuous Function on Non-Closed Intervals
Consider the continuous function
| > |
f2 := cos(x):
f(x) = f2;
|
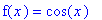
on the open, bounded interval ( 0,
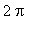 ).
).
| > |
plot( f2, x=0..2*Pi,
title="Continuous Function on an Open Interval that does Not Attain Its Global Maximum on (0,2*Pi)" );
|
![[Maple Plot]](images/GlobalAnalysis46.gif)
We know the cosine function is continuous on every interval of the real numbers. The interval ( 0,
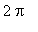 ) is bounded, but open. Because neither
) is bounded, but open. Because neither
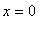 nor
nor
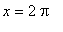 is in the interval, this function
does not attain its global maximum on
( 0,
is in the interval, this function
does not attain its global maximum on
( 0,
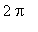 ). The fact that
). The fact that
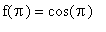 = -1 shows the function does attain its global minimum in the inteval ( 0,
= -1 shows the function does attain its global minimum in the inteval ( 0,
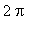 ).
).
Note that if either endpoint is included in the interval, then the function in this example attains both global extrema.
Example 3: Continuous Function on Unbounded Interval
For this example, consider
| > |
f3 := (1-x^2)/(1+x^2):
f(x) = f3;
|
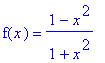
on the unbounded interval (
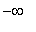 ,
,
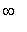 ). (Technically, this interval is both open and closed.)
). (Technically, this interval is both open and closed.)
| > |
plot( f3, x=-10..10,
title="Continuous Function that does Not Attain its Global Minimum on (-infinity,infinity)" );
|
![[Maple Plot]](images/GlobalAnalysis56.gif)
The global maximum for this function on the entire real line is
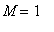 ; the global minimum is
; the global minimum is
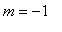 . The global maximum is attained at
. The global maximum is attained at
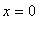 but there is no real number for which
but there is no real number for which
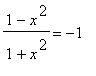 .
.
Example 4: A Final Example
Define the function
| > |
f4 := 1/x^2:
f(x) = f4;
|
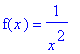
for all
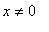 . This function is continuous on any interval that does not include the origin. On an interval
. This function is continuous on any interval that does not include the origin. On an interval
![[a, b]](images/GlobalAnalysis63.gif) with
with
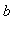 >
>
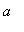 > 0, the global extrema of f on
> 0, the global extrema of f on
![[a, b]](images/GlobalAnalysis66.gif) are
are
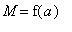 =
=
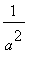 and
and
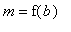 =
=
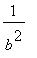 .
.
| > |
plot( f4, x=0.1..1, y=0..100,
title="Continuous Function on Closed and Bounded Interval" );
|
![[Maple Plot]](images/GlobalAnalysis71.gif)
If
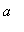 <
<
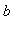 < 0, then
< 0, then
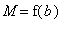 =
=
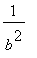 and
and
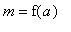 =
=
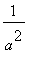 .
.
| > |
plot( f4, x=-3..-1, y=0..2, view=[-3..0,0..2],
title="Continuous Function on Closed and Bounded Interval" );
|
![[Maple Plot]](images/GlobalAnalysis78.gif)
In either case, if one or both endpoint is omitted from the interval, the interval is no longer closed and the corresponding global extrema is no longer attained from the interval.
The function is discontinuous on any interval that contains the origin. If an endpoint of the interval is 0 then the global maximum on this interval is
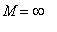 . An infinite extrema can never be attained!
. An infinite extrema can never be attained!
Each of these results is consistent with the stated theorem.
Point 2: Where Do Global Extrema Occur?
Knowing when the global extrema are attained is important. In the examples the identification of the global extrema was based on looking at a graph of the function on the specified domain. While a graph can be useful in identifying global extrema, this is putting the carriage in front of the horse. Knowledge about the global extrema is generally used to select the viewing window for the graph. So, the real question is:
How can we determine the global extrema of a continuous function
on a closed and bounded interval
without looking at a graph
?
Theorem: Global Max/Min Location Theorem
Let f be a function defined on an interval
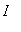 . If an extreme value of f on
. If an extreme value of f on
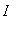 is attained at a point
is attained at a point
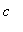 in the interval, then
in the interval, then
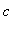 must be a critical point of f on
must be a critical point of f on
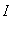 .
.
Example 5:
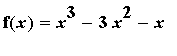 on [ -2, 2 ]
on [ -2, 2 ]
Find the global extrema and their location(s) for
| > |
f5 := x^3 - 3*x^2 - x:
f(x) = f5;
|
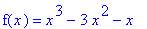
on the interval
| > |
I5 := [-2,2]:
`I` = I5;
|
![I = [-2, 2]](images/GlobalAnalysis107.gif)
This function is continuous on a closed and bounded interval so both global extrema are attained. We have just learned that the only possible locations for extrema to occur are
-
the endpoints of the interval
-
any stationary points of the function that are in the interval
-
or any singular points located in the interval (but polynomials have no singular points)
For this example, there are no singular points (no polynomial has a singular points),
the stationary points are the solutions endpoints are the solutions to
| > |
df5 := diff( f5, x ):
q1 := df5 = 0:
q1;
|
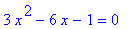
The two solutions to this quadratic equation are
| > |
stat5 := solve( df5=0, x ):
stat5;
|
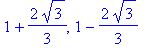
and the endpoints of the interval are
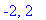
The complete set of possible locations for the global extrema is formed from these lists with all points outside the interval removed
| > |
crit5 := select( InInterval, [ end5, stat5, sing5 ], I5 );
|
![crit5 := [-2, 2, 1-2/3*3^(1/2)]](images/GlobalAnalysis111.gif)
(Note that one of the critical points is outside this interval; it is no longer being considered.)
All that remains is to evaluate the function at each of these points:
| > |
f5a := unapply( f5, x ):
q2 := seq( [ X, simplify(f5a(X)) ], X=crit5 );
|
![q2 := [-2, -18], [2, -6], [1-2/3*3^(1/2), -3+16/9*3^(1/2)]](images/GlobalAnalysis112.gif)
or, in floating point form,
![[-2., -18.], [2., -6.], [-.155, .79e-1]](images/GlobalAnalysis113.gif)
The largest function value is
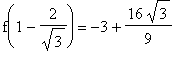 and the smallest function value is
and the smallest function value is
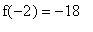 . That is, the global maximum occurs at the critical point
. That is, the global maximum occurs at the critical point
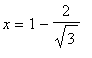 and the global minimum occurs at the left endpoint
and the global minimum occurs at the left endpoint
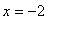 . These results are confirmed with a plot.
. These results are confirmed with a plot.
![[Maple Plot]](images/GlobalAnalysis118.gif)
Example 6:
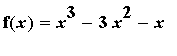 on [ -1, 3 ]
on [ -1, 3 ]
Consider the same cubic function as in Example 5
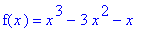
but on the interval
| > |
I6 := [-1,3]:
`I` = I6;
|
![I = [-1, 3]](images/GlobalAnalysis121.gif)
This function is continuous on a closed and bounded interval so both global extrema are attained. The possible locations for extrema to occur are
-
the endpoints of the interval
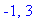
-
any stationary points (solutions to
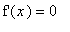 outside the interval will be excluded later)
outside the interval will be excluded later)
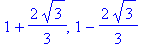
-
or any singular points (but polynomials have no singular points).
The complete set of possible locations for the global extrema is formed from these lists with all points outside the interval removed
| > |
crit6 := select( InInterval, [ end6, stat6, sing6 ], I6 );
|
![crit6 := [-1, 3, 1+2/3*3^(1/2), 1-2/3*3^(1/2)]](images/GlobalAnalysis125.gif)
All that remains is to evaluate the function at each of these points:
| > |
f6a := f5a:
q3 := seq( [ X, simplify(f6a(X)) ], X=crit6 );
|
![q3 := [-1, -3], [3, -3], [1+2/3*3^(1/2), -3-16/9*3^(1/2)], [1-2/3*3^(1/2), -3+16/9*3^(1/2)]](images/GlobalAnalysis126.gif)
or, in floating point form,
![[-1., -3.], [3., -3.], [2.155, -6.079], [-.155, .79e-1]](images/GlobalAnalysis127.gif)
The largest function value is still
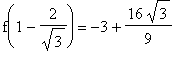 but the smallest function value is now
but the smallest function value is now
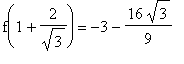 . That is, the global maximum occurs at the critical point
. That is, the global maximum occurs at the critical point
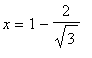 and the global minimum occurs at the other critical point
and the global minimum occurs at the other critical point
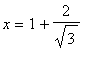 . These results are confirmed with a plot.
. These results are confirmed with a plot.
![[Maple Plot]](images/GlobalAnalysis132.gif)
Example 7:
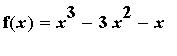 on [ 1, 3 ]
on [ 1, 3 ]
Consider the same cubic function as in Examples 5 and 6
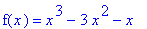
but on the interval
![I = [1, 3]](images/GlobalAnalysis135.gif)
This function is continuous on a closed and bounded interval so both global extrema are attained. The possible locations for extrema to occur are
-
the endpoints of the interval
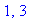
-
any stationary points (solutions to
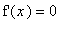 outside the interval will be excluded later)
outside the interval will be excluded later)
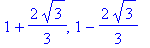
-
or any singular points located in the interval (but polynomials have no singular points).
The complete set of possible locations for the global extrema is formed from these lists with all points outside the interval removed
| > |
crit7 := select( InInterval, [ end7, stat7, sing7 ], I7 );
|
![crit7 := [1, 3, 1+2/3*3^(1/2)]](images/GlobalAnalysis139.gif)
All that remains is to evaluate the function at each of these points:
| > |
f7a := f5a:
q4 := seq( [ X, simplify(f7a(X)) ], X=crit7 );
|
![q4 := [1, -3], [3, -3], [1+2/3*3^(1/2), -3-16/9*3^(1/2)]](images/GlobalAnalysis140.gif)
or, in floating point form,
![[1., -3.], [3., -3.], [2.155, -6.079]](images/GlobalAnalysis141.gif)
The largest function value is now -3, attained at both
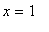 and
and
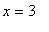 and the smallest function value is
and the smallest function value is
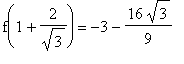 . That is, the global maximum occurs at both endpoints
. That is, the global maximum occurs at both endpoints
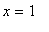 and
and
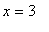 and the global minimum occurs at the critical point in this interval,
and the global minimum occurs at the critical point in this interval,
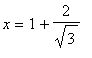 . These results are confirmed with a plot.
. These results are confirmed with a plot.
| > |
plot( f7, x=1..3, view=[0..4,-7..0] );
|
![[Maple Plot]](images/GlobalAnalysis148.gif)
Example 8:
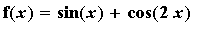 on
on
![[-Pi, 2*Pi]](images/GlobalAnalysis150.gif)
Consider the trigonometric function
| > |
f8 := sin(x)+cos(2*x):
f(x) = f8;
|
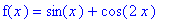
on the interval
| > |
I8 := [-Pi,2*Pi]:
`I` = I8;
|
![I = [-Pi, 2*Pi]](images/GlobalAnalysis152.gif)
Notice that this function is periodic with period
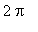 and that the given interval is one and a half periods; remember to check for this when the plot is created.
and that the given interval is one and a half periods; remember to check for this when the plot is created.
This function is continuous on a closed and bounded interval so both global extrema are attained. The possible locations for extrema to occur are
-
the endpoints of the interval
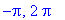
-
any stationary points (any solutions to
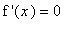 outside the interval will be excluded later)
outside the interval will be excluded later)
| > |
df8 := collect(diff( f8, x ),[sin,cos]):
`f'`(x) = df8;
|
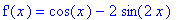
| > |
q1 := df8 = 0:
q2 := solve( q1, x ):
q2;
|
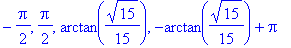
Notice that these are the solutions in the interval
![[-Pi, Pi]](images/GlobalAnalysis158.gif) . By periodicity, the corresponding stationary points in
. By periodicity, the corresponding stationary points in
![[Pi, 3*Pi]](images/GlobalAnalysis159.gif) are obtained by adding
are obtained by adding
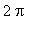 to each stationary point in
to each stationary point in
![[-Pi, Pi]](images/GlobalAnalysis161.gif) .
.
| > |
q3 := op(map( x->x+2*Pi, [q2] ));
|
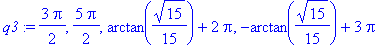
The complete set of stationary points in
![[-Pi, 3*Pi]](images/GlobalAnalysis163.gif) is
is
| > |
stat8 := op( { q2, q3 } ):
stat8;
|
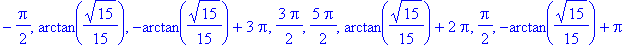
-
or any singular points located in the interval (both sine and cosine are defined for all real numbers)
The complete set of possible locations for the global extrema is formed from these lists with all points outside the interval removed
| > |
crit8 := select( InInterval, [ end8, stat8, sing8 ], evalf(I8) );
|
![crit8 := [-Pi, 2*Pi, -1/2*Pi, arctan(1/15*15^(1/2)), 3/2*Pi, 1/2*Pi, -arctan(1/15*15^(1/2))+Pi]](images/GlobalAnalysis165.gif)
All that remains is to evaluate the function at each critical point:
| > |
f8a := unapply( f8, x ):
q4 := seq( [ X, simplify(f8a(X)) ], X=crit8 );
|
![q4 := [-Pi, 1], [2*Pi, 1], [-1/2*Pi, -2], [arctan(1/15*15^(1/2)), 9/8], [3/2*Pi, -2], [1/2*Pi, 0], [-arctan(1/15*15^(1/2))+Pi, 9/8]](images/GlobalAnalysis166.gif)
or, in floating point form,
![[-3.142, 1.], [6.284, 1.], [-1.571, -2.], [.2527, 1.125], [4.713, -2.], [1.571, 0.], [2.889, 1.125]](images/GlobalAnalysis167.gif)
The largest function value is now
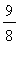 , attained at both
, attained at both
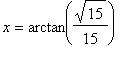 and
and
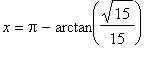 and the smallest function value is -2 which is attained at
and the smallest function value is -2 which is attained at
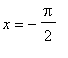 and
and
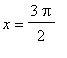 . That is, the global maximum occurs at the stationary points
. That is, the global maximum occurs at the stationary points
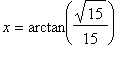 = 0.2527 and
= 0.2527 and
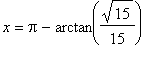 = 2.8889 and the global minimum occurs at the stationary points,
= 2.8889 and the global minimum occurs at the stationary points,
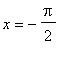 = -1.5708 and
= -1.5708 and
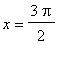 = 4.7124. These results are confirmed with a plot.
= 4.7124. These results are confirmed with a plot.
| > |
plot( f8, x=-Pi..2*Pi );
|
![[Maple Plot]](images/GlobalAnalysis177.gif)
This plot does appear to be periodic with period
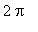 . This point is further emphasized with a plot over a larger interval.
. This point is further emphasized with a plot over a larger interval.
| > |
plot( f8, x=-3*Pi..3*Pi );
|
![[Maple Plot]](images/GlobalAnalysis179.gif)
Example 9:
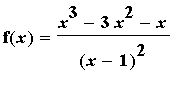 on [ -3, 1 )
on [ -3, 1 )
Consider a new function created from the polynomial first encountered in Example 5.
| > |
f9 := f5/(x-1)^2:
f(x) = f9;
|
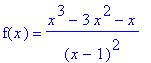
on the interval [-3,1).
| > |
I9 := [-3,1]:
`I` = I9;
|
![I = [-3, 1]](images/GlobalAnalysis182.gif)
Note that this interval is not closed. It is not possible to simply add the right endpoint to the interval;
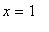 is not in the domain of the function. Because the interval is not closed, the theorem does not apply. But, a slight modification to our approach can still be used. First, because
is not in the domain of the function. Because the interval is not closed, the theorem does not apply. But, a slight modification to our approach can still be used. First, because
| > |
q1 := Limit( f9, x=1, left ):
q1 = value( q1 );
|
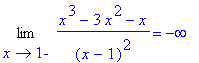
it is clear that there will be no (finite) global minimum (
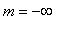 ). The global maximum should exist (i.e., be finite) and will occur at a critical point:
). The global maximum should exist (i.e., be finite) and will occur at a critical point:
-
the endpoints of the interval (note that -1 is not included here)
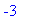
-
any stationary points of the function
| > |
df9 := simplify(diff( f9, x )):
`f'`(x) = df9;
|
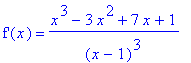
| > |
q1 := df9 = 0:
stat9 := solve( q1, x ):
stat9;
|
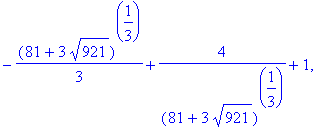
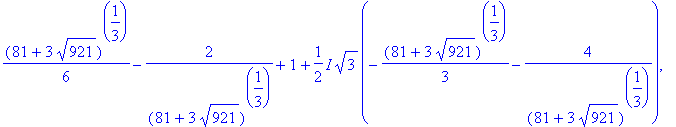
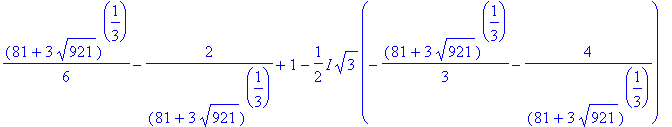
-
or any singular points located in the interval (as mentioned previously,
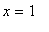 is not in the half-open interval, so is not considered here)
is not in the half-open interval, so is not considered here)
The complete set of possible locations for the global extrema is formed from these lists with all points outside the interval removed
| > |
crit9 := select( InInterval, [ end9, stat9, sing9 ], I9 ):
crit9;
|
![[-3, -1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1]](images/GlobalAnalysis192.gif)
All that remains is to evaluate the function at each of these points:
| > |
f9a := unapply( f9, x ):
q2 := seq( [ X, simplify(f9a(X)) ], X=crit9 );
|
![q2 := [-3, -51/16], [-1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1, 9*(-729-27*921^(1/2)+216*(81+3*921^(1/2))^(1/3)+8*(81+3*921^(1/2))^(1/3)*921^(1/2)-32*(81+3*921^(1/2))^(2/3))/(81+3*921^(1/2...](images/GlobalAnalysis193.gif)
![q2 := [-3, -51/16], [-1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1, 9*(-729-27*921^(1/2)+216*(81+3*921^(1/2))^(1/3)+8*(81+3*921^(1/2))^(1/3)*921^(1/2)-32*(81+3*921^(1/2))^(2/3))/(81+3*921^(1/2...](images/GlobalAnalysis194.gif)
![q2 := [-3, -51/16], [-1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1, 9*(-729-27*921^(1/2)+216*(81+3*921^(1/2))^(1/3)+8*(81+3*921^(1/2))^(1/3)*921^(1/2)-32*(81+3*921^(1/2))^(2/3))/(81+3*921^(1/2...](images/GlobalAnalysis195.gif)
or, in floating point form,
![[-3., -3.188], [-.134, .5961e-1]](images/GlobalAnalysis196.gif)
The global maximum occurs for
 = -0.134 with a maximum value just slightly larger than 0. These results are confirmed with a plot.
= -0.134 with a maximum value just slightly larger than 0. These results are confirmed with a plot.
| > |
plot( f9, x=-3..1, y=-50..10 );
|
![[Maple Plot]](images/GlobalAnalysis198.gif)
Note that while the graph makes it appear that the function might be negative (or non-positive) for all
 < 1 with a maximum at the origin, this is close but not completely accurate.
< 1 with a maximum at the origin, this is close but not completely accurate.
Example 10:
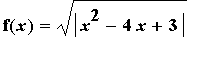 on [ -2, 4 ]
on [ -2, 4 ]
For our final example, find the global extrema (and where they occur) of
| > |
f10 := sqrt( abs(x^2-4*x+3) ):
f(x) = f10;
|
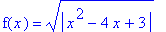
on the interval
| > |
I10 := [-2,4]:
`I` = I10;
|
![I = [-2, 4]](images/GlobalAnalysis202.gif)
Because the absolute value function returns non-negative values, this function is defined on the entire real line. In particular, the fact that the function is continuous on the closed and bounded interval [-2, 4] means that it will attain its global extrema somewhere in this interval. As usual, the search begins by locating all critical points in the interval:
-
the endpoints of the interval
| > |
end10 := op(I10):
end10;
|
-
any stationary points of the function
| > |
df10 := simplify(diff( f10, x )):
`f'`(x) = convert(df10,piecewise,x);
|
![`f'`(x) = PIECEWISE([(-2+x)/(x^2-4*x+3)^(1/2), x < 1],[undefined, x = 1],[-(-2+x)/(-3-x^2+4*x)^(1/2), x < 3],[undefined, x = 3],[(-2+x)/(x^2-4*x+3)^(1/2), 3 < x])](images/GlobalAnalysis204.gif)
| > |
q1 := df10 = 0:
stat10 := solve( q1, x ):
stat10;
|
-
or any singular points (from the above display, it is clear that the derivative does not exist for
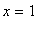 and
and
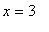 --- these are the roots of
--- these are the roots of
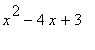 )
)
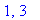
The complete set of possible locations for the global extrema is formed from these lists with all points outside the interval removed
| > |
crit10 := select( InInterval, [ end10, stat10, sing10 ], I10 ):
crit10;
|
![[-2, 4, 2, 1, 3]](images/GlobalAnalysis210.gif)
All that remains is to evaluate the function at each of these points:
| > |
f10a := unapply( f10, x ):
q2 := seq( [ X, simplify(f10a(X)) ], X=crit10 );
|
![q2 := [-2, 15^(1/2)], [4, 3^(1/2)], [2, 1], [1, 0], [3, 0]](images/GlobalAnalysis211.gif)
or, in floating point form,
![[-2., 3.873], [4., 1.732], [2., 1.], [1., 0.], [3., 0.]](images/GlobalAnalysis212.gif)
The global maximum
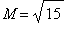 occurs for
occurs for
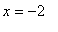 and the global minimum
and the global minimum
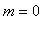 occurs at each singular point
occurs at each singular point
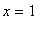 and
and
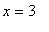 . These results are confirmed with a plot.
. These results are confirmed with a plot.
![[Maple Plot]](images/GlobalAnalysis218.gif)
![]() .
.
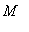 is the
global maximum value
of
f
on
is the
global maximum value
of
f
on
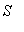 if
if
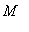 is the smallest number such that
is the smallest number such that
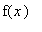 <=
<=
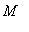 for all
for all
 in
in
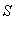 .
.
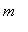 is the
global minimum value
of
f
on
is the
global minimum value
of
f
on
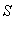 if
if
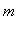 is the largest number suc that
is the largest number suc that
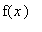 >=
>=
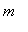 for all
for all
 in
in
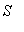 .
.
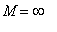 and
and
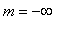 then every function has both a global maximum and a global minimum.
then every function has both a global maximum and a global minimum.
![f1 := PIECEWISE([x, x < 1],[1/2*x-1/2, x < 2])](images/GlobalAnalysis23.gif)
![[Maple Plot]](images/GlobalAnalysis25.gif)
![[Maple Plot]](images/GlobalAnalysis46.gif)
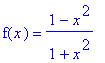
![[Maple Plot]](images/GlobalAnalysis56.gif)
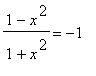 .
.
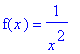
![[Maple Plot]](images/GlobalAnalysis71.gif)
![[Maple Plot]](images/GlobalAnalysis78.gif)
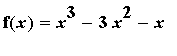 on [ -2, 2 ]
on [ -2, 2 ]
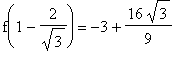 and the smallest function value is
and the smallest function value is
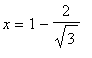 and the global minimum occurs at the left endpoint
and the global minimum occurs at the left endpoint
![[Maple Plot]](images/GlobalAnalysis118.gif)
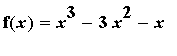 on [ -1, 3 ]
on [ -1, 3 ]
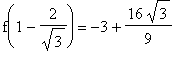 but the smallest function value is now
but the smallest function value is now
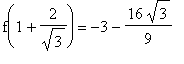 . That is, the global maximum occurs at the critical point
. That is, the global maximum occurs at the critical point
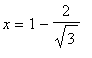 and the global minimum occurs at the other critical point
and the global minimum occurs at the other critical point
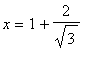 . These results are confirmed with a plot.
. These results are confirmed with a plot.
![[Maple Plot]](images/GlobalAnalysis132.gif)
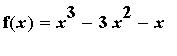 on [ 1, 3 ]
on [ 1, 3 ]
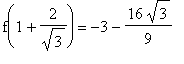 . That is, the global maximum occurs at both endpoints
. That is, the global maximum occurs at both endpoints
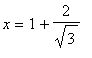 . These results are confirmed with a plot.
. These results are confirmed with a plot.
![[Maple Plot]](images/GlobalAnalysis148.gif)
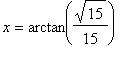 and
and
 and the smallest function value is -2 which is attained at
and the smallest function value is -2 which is attained at
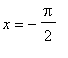 and
and
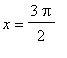 . That is, the global maximum occurs at the stationary points
. That is, the global maximum occurs at the stationary points
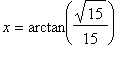 = 0.2527 and
= 0.2527 and
 = 2.8889 and the global minimum occurs at the stationary points,
= 2.8889 and the global minimum occurs at the stationary points,
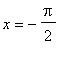 = -1.5708 and
= -1.5708 and
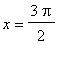 = 4.7124. These results are confirmed with a plot.
= 4.7124. These results are confirmed with a plot.
![[Maple Plot]](images/GlobalAnalysis177.gif)
![[Maple Plot]](images/GlobalAnalysis179.gif)
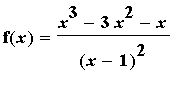 on [ -3, 1 )
on [ -3, 1 )
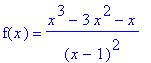
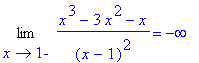
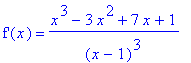
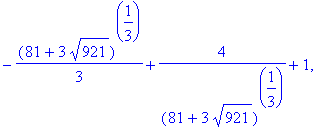
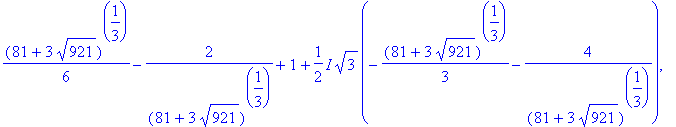
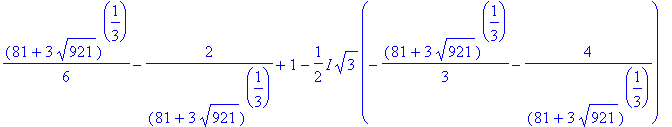
![[-3, -1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1]](images/GlobalAnalysis192.gif)
![q2 := [-3, -51/16], [-1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1, 9*(-729-27*921^(1/2)+216*(81+3*921^(1/2))^(1/3)+8*(81+3*921^(1/2))^(1/3)*921^(1/2)-32*(81+3*921^(1/2))^(2/3))/(81+3*921^(1/2...](images/GlobalAnalysis193.gif)
![q2 := [-3, -51/16], [-1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1, 9*(-729-27*921^(1/2)+216*(81+3*921^(1/2))^(1/3)+8*(81+3*921^(1/2))^(1/3)*921^(1/2)-32*(81+3*921^(1/2))^(2/3))/(81+3*921^(1/2...](images/GlobalAnalysis194.gif)
![q2 := [-3, -51/16], [-1/3*(81+3*921^(1/2))^(1/3)+4/(81+3*921^(1/2))^(1/3)+1, 9*(-729-27*921^(1/2)+216*(81+3*921^(1/2))^(1/3)+8*(81+3*921^(1/2))^(1/3)*921^(1/2)-32*(81+3*921^(1/2))^(2/3))/(81+3*921^(1/2...](images/GlobalAnalysis195.gif)
![[Maple Plot]](images/GlobalAnalysis198.gif)
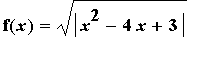 on [ -2, 4 ]
on [ -2, 4 ]
![`f'`(x) = PIECEWISE([(-2+x)/(x^2-4*x+3)^(1/2), x < 1],[undefined, x = 1],[-(-2+x)/(-3-x^2+4*x)^(1/2), x < 3],[undefined, x = 3],[(-2+x)/(x^2-4*x+3)^(1/2), 3 < x])](images/GlobalAnalysis204.gif)
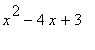 )
)
![[Maple Plot]](images/GlobalAnalysis218.gif)