Derivation and Discussion of the Chain Rule
Let F be a function formed as the composition of f with g:
![]() . (The precise requirements on f and g will be discussed later.) To determine the derivative of F in terms of f, g, and their derivatives, look at the definition:
. (The precise requirements on f and g will be discussed later.) To determine the derivative of F in terms of f, g, and their derivatives, look at the definition:
| > | F := x -> f(g(x)): dq1 := (F(x+h)-F(x)): dF1 := Limit( dq1/h, h=0 ): `F'`(x) = dF1; |
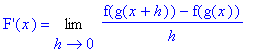
Assuming g is differentiable at
![]() , then g must be continuous at
, then g must be continuous at
![]() and so, for small values of
and so, for small values of
![]() ,
,
![]() can be approximated by
can be approximated by
![]() . Making this substitution in the difference quotient for the definition of
. Making this substitution in the difference quotient for the definition of
![]() yields:
yields:
| > | q1 := g(x+h) = g(x)+`g'`(x)*h: dq2 := eval( dq1, q1 ): dF2 := Limit( dq2/h, h=0 ): `F'`(x) = dF2; |
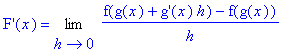
This limit can be massaged into a form that is recognizable as a derivative if we let
| > | q2 := r = `g'`(x)*h: q2; |
![]()
With this substitution we can now write
| > | dF3a := eval( dq2/h, isolate(q2,h) ): dF3 := Limit( dF3a, h=0 ): `F'`(x) = dF3; |
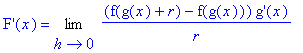
This looks promising. Because
![]() is a constant (and finite) it can be factored out of the limit. Moreover, the limit as
is a constant (and finite) it can be factored out of the limit. Moreover, the limit as
![]() approaches 0 can be equivalently stated as a limit as
approaches 0 can be equivalently stated as a limit as
![]() approaches 0. Thus,
approaches 0. Thus,
| > | dq4 := dq3/`g'`(x): dF4 := Limit( dq4, r=0 ) * `g'`(x): `F'`(x) = dF4; |

Aha! The limit that remains can now be identified as the derivative of f, evaluated at
![]() :
:
![]() . This yields one form of the Chain Rule:
. This yields one form of the Chain Rule:
![]()
Theorem: The Chain Rule
Let f and g be differentiable functions such that
![]() and
and
![]() both exist. Then the composition of f with g,
both exist. Then the composition of f with g,
![]() , is differentiable at
, is differentiable at
![]() and the derivative of F at
and the derivative of F at
![]() is
is
![]() .
.
| > |
There are quite a few ways to interpret and understand the Chain Rule. One of the most useful is to think of the composition as a gear. For example, if a chain is being pulled through a 53-tooth gear and if the gear is being turned at a rate of 100 revolutions per minute then the chain passes through the gear at a rate of (53 links/revolution)(100 revolutions/min) = 5300 links/min. Note how the composite rate is the product of the individual rates.
Another way to look at the Chain Rule is to write
![]() as
as
![]() and
and
![]() . Then,
. Then,
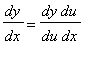
This perspective is very useful and can help you to remember the Chain Rule formula. You must be aware that even though it is tempting to justify this formula by canceling
![]() from numerator and denominator, the real ``proof'' of this result must be stated in terms of difference quotients (where we really do have fractions!). Here is a sketch of that proof (with additional steps at the beginning and end to emphasize the connection to the first form of the Chain Rule):
from numerator and denominator, the real ``proof'' of this result must be stated in terms of difference quotients (where we really do have fractions!). Here is a sketch of that proof (with additional steps at the beginning and end to emphasize the connection to the first form of the Chain Rule):
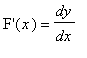
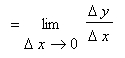
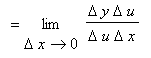
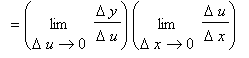
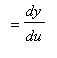
![]()
![]()
![]()
| > |
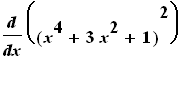
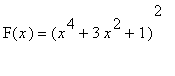 =
=
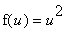 and
and
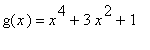 .
.
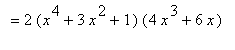
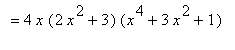 .
.
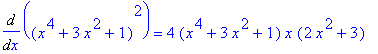
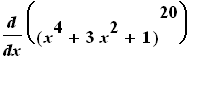
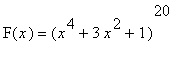 =
=
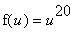 and
and
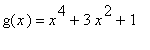 .
.
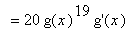
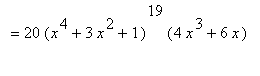
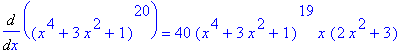
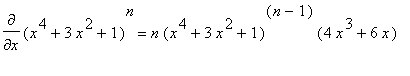 .
.
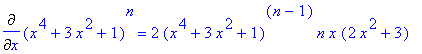
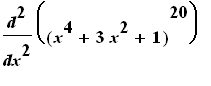 and Other Higher Derivatives
and Other Higher Derivatives
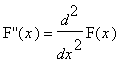
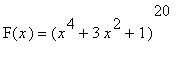
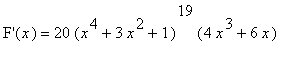 .
.
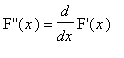
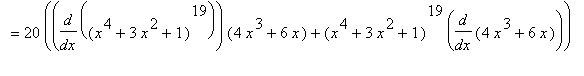
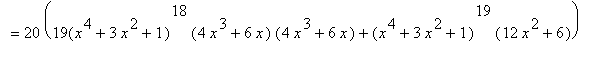
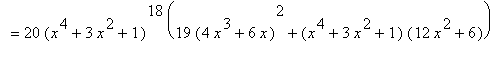
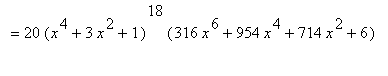
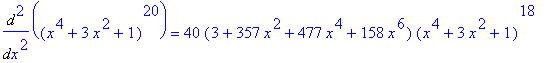
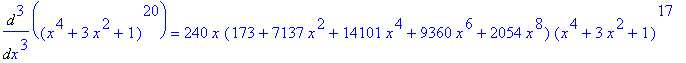
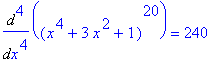
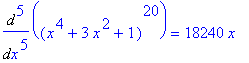
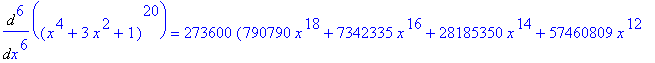
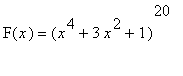 is a polynomial of degree 80, the 80-th derivative of F,
is a polynomial of degree 80, the 80-th derivative of F,
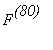 , should be have degree 80-80=0
, should be have degree 80-80=0
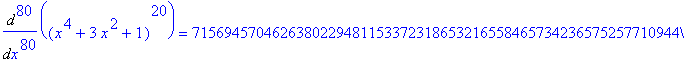
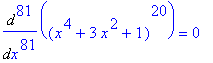
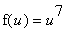 and
and
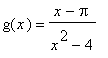 so that
so that
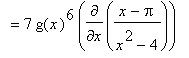
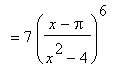
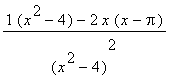
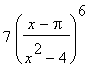
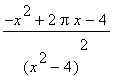
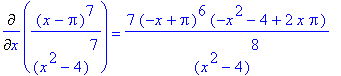
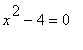 , i.e.
, i.e.