Point 1: First Derivative Determines Increasing/Decreasing
The definition of an increasing and decreasing function is fairly intuitive. However, it is easiest to implement when a graph of the function is available. The fact that
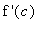 is the slope of the tangent line to the graph of
is the slope of the tangent line to the graph of
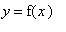 at the point (
at the point (
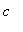 ,
,
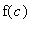 ) suggests that the first derivative should be useful in determining if a function is increasing or decreasing on an interval containing
) suggests that the first derivative should be useful in determining if a function is increasing or decreasing on an interval containing
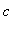 . The formal connection between increasing/decreasing and the first derivative is contained in the following theorem.
. The formal connection between increasing/decreasing and the first derivative is contained in the following theorem.
Theorem: Increasing/Decreasing Test
Let f be a function that is
-
continuous on an interval
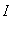 and
and
-
differentiable on
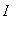 (except possibly at the endpoints).
(except possibly at the endpoints).
Then:
-
if
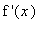 > 0 for all
> 0 for all
 in
in
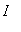 (except possibly at the endpoints), then f is increasing on
(except possibly at the endpoints), then f is increasing on
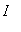
-
if
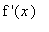 < 0 for all
< 0 for all
 in
in
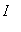 (except possibly at the endpoints), then f is decreasing on
(except possibly at the endpoints), then f is decreasing on
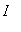
Notes
The sign of the derivative at the endpoints is not important.
In fact, it is not a problem if the derivative does not exist at one or both endpoints.
Example 1:
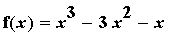
Find the intervals on which the function
| > |
f1 := x^3 - 3*x^2 - x:
f(x) = f1;
|
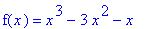
is increasing and decreasing.
Because all polynomials are continuous on the entire real line, this function -- and all of its derivatives -- are automatically continuous for all values of
 .
.
Recall that in the
GlobalAnalysis lesson (Example 5) it was found that this function has two stationary points.
| > |
df1 := diff( f1, x ):
`f'`(x) = df1;
|
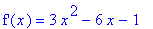
| > |
stat1 := solve( df1 = 0, x ):
stat1;
|
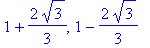
Because the derivative is continuous, the
Intermediate Value Theorem allows us to conclude that the derivative will have one sign on each of the following three intervals:
(
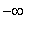 ,
,
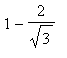 ), (
), (
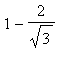 ,
,
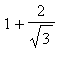 ), and (
), and (
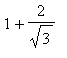 ,
,
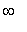 ).
).
To determine on which of these intervals the function is increasing and on which it is decreasing, simply evaluate the derivative at a convenient point in each subinterval. (The
TestIncrDecr
command, defined at the top of this worksheet, evaluates the first derivative at each point and uses the sign of the result to report if the function is increasing or decreasing on the subinterval containing this point (or stationary at the point).)
| > |
testpts1 := [ -1, 0, 3 ]:
TestIncrDecr( df1, testpts1 );
|
f'(-1.)=8.; the function is increasing on the subinterval containing -1.
f'(0.)=-1.; the function is decreasing on the subinterval containing 0.
f'(3.)=8.; the function is increasing on the subinterval containing 3.
Thus, the function
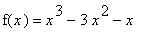 is increasing on (
is increasing on (
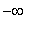 ,
,
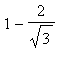 ) and (
) and (
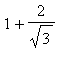 ,
,
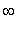 ) and decreasing on (
) and decreasing on (
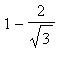 ,
,
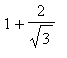 ).
).
Note
Maple's
solve
command can solve some inequalities. In this case, it is able to provide a direct answer to our question.
The function is increasing on

and decreasing on
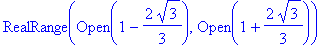
To conclude, the graph of this function with the increasing intervals shown in red and the decreasing interval shown in blue confirms these results.
| > |
p1 := plot( f1, x=-2 ..1-2/sqrt(3), color=red,
legend=["y = f(x): increasing"] ):
p2 := plot( f1, x=1-2/sqrt(3)..1+2/sqrt(3), color=blue,
legend=["y = f(x): decreasing"] ):
p3 := plot( f1, x=1+2/sqrt(3)..4, color=red,
legend=["y = f(x): increasing"] ):
p4 := plot( df1, x=-2 ..4, color=green,
legend=["y = f '(x)"] ):
display( [p1,p2,p3,p4] );
|
![[Maple Plot]](images/LocalAnalysis64.gif)
Observe how the graph of the derivative changes sign precisely where the function changes from increasing to decreasing and later from decreasing to increasing.
Maplets to Determine Intervals where a Function is Increasing/Decreasing
There are a number of maplets that can be used to obtain information about where a function is increasing and decreasing.
CurveAnalysis
[
Maplet Viewer][
MapleNet]
The
CurveAnalysis
maplet can explicitly identify intervals on which a function is increasing or decreasing. To use this maplet to determine the increasing intervals for a function:
-
enter the function (as a function of
 ) and interval (it is best to avoid using infinities but sometimes works with minimal objections)
) and interval (it is best to avoid using infinities but sometimes works with minimal objections)
-
click the button labeled
Show the Increasing Intervals
-
press the
Show
button
The interval(s) on which the function is increasing will be shown in the large box labeled
Points and Intervals
. Note that all intervals appear to be closed intervals.
Obtaining the interval(s) on which the function is decreasing should be apparent. Other features of this maplet will be discussed later in this lesson.
FunctionAnalyzer
[
Maplet Viewer][
MapleNet]
The
FunctionAnalyzer
maplet is similar. It has somewhat greater flexibility but requires a little more from the user. To use this maplet to identify the intervals on which a function is increasing:
-
enter the function in the region labeled
y =
in the
Function
panel
the first and second derivatives will be computed automatically
-
in the
Solve an Equation or Inequality
panel, enter
Dy > 0
in the field labeled
Enter equation to be solved (use y, Dy, D2y)
-
press the
Attempt to solve equation
button
Maple's results will be displayed in the region immediately above the button you just clicked.
A unique feature of the
FunctionAnalyzer
maplet is the ability to create a ``sign chart'' for the first and second derivative of a function. A sign chart can be a particularly effective method to display intervals where a function is increasing or decreasing. To activate this feature:
-
click the Show sign chart box in the First Derivative panel
-
in the fields to the right of the label
Horizontal Axis
, enter the endpoints of the interval and the name of the independent variable
-
press the
Update plot
button
The plotting window will display an empty set of axes except for a horizontal line near the bottom. The function is increasing wherever this line is red and decreasing wherever this line is blue. This is the sign chart for the first derivative.
To include the function and/or first derivative in the plot, click the appropriate
Include in plot
buttons in the
Function
and
First Derivative
panels, then press the
Update plot
button.
DerivativePlot
[
Maplet Viewer][
MapleNet]
The
DerivativePlot
maplet has a very simple purpose - for a given function, create a graph showing almost any combination of the function and its derivatives. For example, to display a graph of a function and its first derivative:
-
enter the
Function
(it is not necessary to enter the range in the
a =
and
b =
fields)
-
change the
orders
field to
[ 1 ]
(the square brackets are needed)
-
in the
Display Options
panel, click the
Show function
and
Show derivatives
buttons
-
also in the
Display Options
panel, enter the viewing window
-
press the Plot button
The
Plot Window
will be updated to contain a plot of the function and its first derivative on the specified interval. (By default, the function will be plotted in red. For this reason it is recommended that you not use red as a color to display a derivative.)
Example 2:
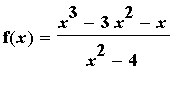
Find the intervals on which the function
| > |
f2 := (x^3 - 3*x^2 - x)/(x^2-4):
f(x) = f2;
|
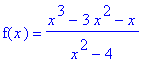
is increasing and decreasing.
This function is continuous, and differentiable, for all real numbers
 except
except
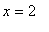 and
and
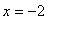 .
.
The singularities at
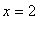 and
and
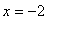 need to be remembered because these are points where the derivative could jump from positive to negative, or vice versa.
need to be remembered because these are points where the derivative could jump from positive to negative, or vice versa.
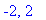
The derivative is
| > |
df2 := simplify(diff( f2, x )):
`f'`(x) = df2;
|
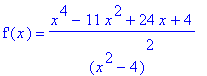
Of the four zeroes of the numerator, there are two real-valued solutions. These are stationary points.
| > |
q1 := solve( numer(df2) = 0, x ):
stat2 := op(remove( has, allvalues([q1]), I )):
evalf[4](stat2);
|
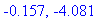
By the continuity of the derivative and the
Intermediate Value Theorem, the derivative can change sign at a point where the derivative is zero (a stationary point) or where the function and/or derivative is not defined (a singular point). Thus, the real line is divided into the following five intervals on which the function is either increasing or decreasing:
(
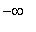 , -4.08 ), ( -4.08, -2 ), ( -2, -0.16 ), ( -0.16, 2 ), ( 2,
, -4.08 ), ( -4.08, -2 ), ( -2, -0.16 ), ( -0.16, 2 ), ( 2,
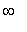 )
)
To determine on which of these intervals the function is increasing and on which it is decreasing, simply evaluate the derivative at a convenient point in each subinterval.
| > |
testpts2 := [ -5, -3, -1, 1, 3 ]:
TestIncrDecr( df2, testpts2 );
|
f'(-5.)=.5306; the function is increasing on the subinterval containing -5.
f'(-3.)=-3.440; the function is decreasing on the subinterval containing -3.
f'(-1.)=-3.333; the function is decreasing on the subinterval containing -1.
f'(1.)=2.000; the function is increasing on the subinterval containing 1.
f'(3.)=2.320; the function is increasing on the subinterval containing 3.
Thus, the function
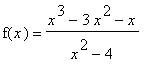 is increasing on (
is increasing on (
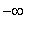 , -4.08 ), ( -0.16, 2 ), and ( 2,
, -4.08 ), ( -0.16, 2 ), and ( 2,
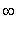 ) and decreasing on ( -4.08, -2 ) and ( -2, -0.16 ). Because
) and decreasing on ( -4.08, -2 ) and ( -2, -0.16 ). Because
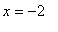 is not in the domain of this function, it would be incorrect to say that this function is increasing on ( -0.16,
is not in the domain of this function, it would be incorrect to say that this function is increasing on ( -0.16,
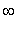 ).
).
Note
Using Maple's
solve
command, the function is found to be increasing on

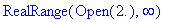
and decreasing on
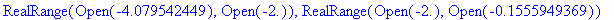
Note the use of the floating point zero,
0.
, to force Maple to report floating-point results. If the integer zero,
0
, is used, Maple's output is rather imposing -- but exact! (Try it!)
To conclude, the graph of this function with the increasing intervals shown in red and the decreasing interval shown in blue confirms these results.
| > |
p1 := plot( f2, x=-16 ..-4.08, color=red,
legend=["y = f(x): increasing"] ):
p2 := plot( f2, x=-4.08..-2, color=blue,
legend=["y = f(x): decreasing"] ):
p3 := plot( f2, x=-2 ..-0.16, color=blue,
legend=["y = f(x): decreasing"] ):
p4 := plot( f2, x=-0.16.. 2, color=red,
legend=["y = f(x): increasing"] ):
p5 := plot( f2, x= 2 ..16, color=red,
legend=["y = f(x): increasing"] ):
p6 := plot( df2, x=-16 ..16, color=green, discont=true,
legend=["y = f '(x)"] ):
display( [p1,p2,p3,p4,p5,p6], view=[-16..16,-30..20] );
|
![[Maple Plot]](images/LocalAnalysis86.gif)
Observe how the function changes from increasing to decreasing at the two stationary points. Note also that at
 = -2 the function is decreasing on either side but not decreasing on any interval containing points from both sides of the singularity. The same behavior can be seen at
= -2 the function is decreasing on either side but not decreasing on any interval containing points from both sides of the singularity. The same behavior can be seen at
 = 2 except that the function is increasing on both sides of this singularity.
= 2 except that the function is increasing on both sides of this singularity.
Example 3:
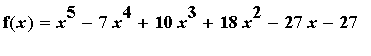
Find the intervals on which the function
| > |
f3 := x^5-7*x^4+10*x^3+18*x^2-27*x-27:
f(x) = f3;
|
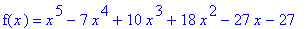
is increasing and decreasing.
Because all polynomials are continuous on the entire real line, this function -- and all of its derivatives -- are automatically continuous for all values of
 .
.
The derivative is the fourth-degree polynomial
| > |
df3 := diff( f3, x ):
`f'`(x) = df3;
|
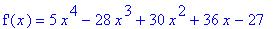
The (four) roots of which are
| > |
stat3 := solve( df3 = 0, x ):
stat3;
|
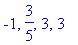
Because the derivative is continuous, the
Intermediate Value Theorem allows us to conclude that the derivative will have one sign on each of the following four intervals:
(
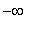 , -1 ), ( -1,
, -1 ), ( -1,
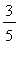 ), (
), (
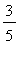 , 3 ), and ( 3,
, 3 ), and ( 3,
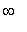 ).
).
To determine on which of these intervals the function is increasing and on which it is decreasing, simply evaluate the derivative at a convenient point in each subinterval.
| > |
testpts3 := [ -2, 0, 2, 4 ]:
TestIncrDecr( df3, testpts3 );
|
f'(-2.)=325.; the function is increasing on the subinterval containing -2.
f'(0.)=-27.; the function is decreasing on the subinterval containing 0.
f'(2.)=21.; the function is increasing on the subinterval containing 2.
f'(4.)=85.; the function is increasing on the subinterval containing 4.
Thus, the function
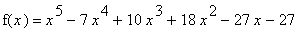 is increasing on (
is increasing on (
 , -1 ), (
, -1 ), (
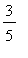 , 3 ), ( 3,
, 3 ), ( 3,
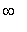 ) and decreasing on ( -1,
) and decreasing on ( -1,
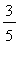 ). Because the function is defined at
). Because the function is defined at
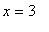 , it would be correct to say the function is increasing on (
, it would be correct to say the function is increasing on (
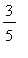 ,
,
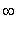 ). This point will be addressed again after the plot of the function and its derivative are obtained.
). This point will be addressed again after the plot of the function and its derivative are obtained.
Note
Using the
solve
command, the function is found to be increasing on

and decreasing on

To conclude, the graph of this function with the increasing intervals shown in red and the decreasing interval shown in blue confirms these results.
| > |
p1 := plot( f3, x=-2 ..-1, color=red,
legend=["y = f(x): increasing"] ):
p2 := plot( f3, x=-1 ..3/5, color=blue,
legend=["y = f(x): decreasing"] ):
p3 := plot( f3, x=3/5..5, color=red,
legend=["y = f(x): increasing"] ):
p4 := plot( df3, x=-2..5, color=green,
legend=["y = f'(x)"] ):
display( [p1,p2,p3,p4], view=[-2..5,-100..200] );
|
![[Maple Plot]](images/LocalAnalysis108.gif)
Observe how the graph of the derivative does not change sign at the stationary point at
 = 3. This zero in the derivative forces the graph of the function to flatten out at this point -- but only at this one point. Technically, the function is still increasing at
= 3. This zero in the derivative forces the graph of the function to flatten out at this point -- but only at this one point. Technically, the function is still increasing at
 = 3 because all function values to the left of
= 3 because all function values to the left of
 = 3 are negative and all function values to the right are positive.
= 3 are negative and all function values to the right are positive.
Point 2: Second Derivative Determines Concavity
In the first part of this lesson we learned that a differentiable function, f, is increasing when its derivative is positive. Applied to the first derivative, we observe that f ' is increasing when (f ')' = f '' is positive.
Theorem: Concave Up/Down Test
Suppose f is a function that is
-
continuous on an interval
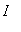 and
and
-
has two derivatives on
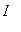 (except possibly at the endpoints)
(except possibly at the endpoints)
Then,
-
if
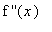 > 0 for all
> 0 for all
 in
in
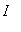 (except possibly the endpoints), then f is concave up on
(except possibly the endpoints), then f is concave up on
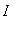
-
if
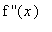 < 0 for all
< 0 for all
 in
in
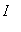 (except possibly the endpoints), then f is concave down on
(except possibly the endpoints), then f is concave down on
Notes:
-
A consequence of this theorem is that an inflection point is a point where the second derivative changes sign. This can be a point where
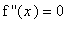 or a point where
or a point where
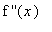 does not exist (but is in the domain of f).
does not exist (but is in the domain of f).
-
Points where
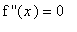 are called
possible
inflection points. It is still necessary to check for the sign change in f '' at this point.
are called
possible
inflection points. It is still necessary to check for the sign change in f '' at this point.
-
The hypotheses can be simplified to "Suppose f is a function that has a second derivative on an interval
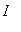 ". If a function has a second derivative on an interval, then the first derivative and the function must both be continuous. The explicit listing of continuity in the statement of the theorem is a reminder to check this property prior to attempting to apply the theorem.
". If a function has a second derivative on an interval, then the first derivative and the function must both be continuous. The explicit listing of continuity in the statement of the theorem is a reminder to check this property prior to attempting to apply the theorem.
Example 4:
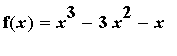
Find the intervals on which the function
| > |
f4 := x^3-3*x^2-x:
f(x) = f4;
|
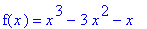
is concave up and concave down; identify any inflection points.
The approach is to use the singular points and possible inflection points (solutions to
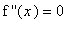 ) to divide the domain into intervals where the second derivative will be either positive or negative on the entire interval.
) to divide the domain into intervals where the second derivative will be either positive or negative on the entire interval.
This is the same function as in Example 1. Once again, the fact that the function is a polynomial means there are no singulararities for this function, or any of its derivatives. The second derivative is
| > |
ddf4 := diff( f4, x,x ):
`f ''`(x) = ddf4;
|
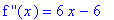
and the possible inflection points are the solutions to
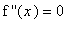 :
:
| > |
possinfl4 := solve( ddf4 = 0, x ):
possinfl4;
|
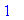
This means the second derivative will have one sign on each of the following two intervals:
(
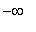 , 1 ) and ( 1,
, 1 ) and ( 1,
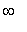 ).
).
To determine if the function concave up or concave down on an interval, simply evaluate the derivative at a convenient point in each subinterval. (The
TestConcavity
command, defined at the top of this worksheet, evaluates the second derivative at each point and uses the sign of the result to report if the function is concave up or concave down (or a possible inflection point).)
| > |
testpts4 := [ 0, 2 ]:
TestConcavity( ddf4, testpts4 );
|
f''(0.)=-6.; the function is concave down on the subinterval containing 0.
f''(2.)=6.; the function is concave up on the subinterval containing 2.
Thus, the function
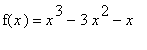 is concave up on ( 1,
is concave up on ( 1,
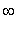 ) and concave down on (
) and concave down on (
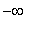 , 1 ).
, 1 ).
Note
Using the
solve
command, the function is found to be concave up on
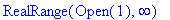
and concave down on
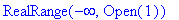
To conclude, the graph of this function with the concave up interval shown in pink and the decreasing interval shown in cyan confirms these results.
| > |
p1 := plot( f4, x=-2..1, color=pink,
legend=["y = f(x): concave up"] ):
p2 := plot( f4, x= 1..4, color=cyan,
legend=["y = f(x): concave down"] ):
p3 := plot( ddf4, x=-2..4, color=turquoise,
legend=["y = f''(x)"] ):
display( [p1,p2,p3] );
|
![[Maple Plot]](images/LocalAnalysis144.gif)
Observe how the graph of the second derivative changes sign precisely where the function changes concavity, at
 = 1.
= 1.
Maplets to Determine Intervals where a Function is Concave Up/Down
The three maplets useful for determining intervals where a function is increasing and decreasing are also appropriate to determine where a function is concave up and down.
CurveAnalysis
[
Maplet Viewer][
MapleNet]
The
CurveAnalysis
maplet contains buttons for computing intervals where the function is concave up and where it is concave down. Likewise, the concavity information can be displayed in the plot. The usage is completely parallel to the usage of this maplet for increasing/decreasing analysis.
FunctionAnalyzer
[
Maplet Viewer][
MapleNet]
The
FunctionAnalyzer
maplet is similar. Use the Second Derivative panel to specify if the plot should include the second derivative and/or the sign chart for f ''. To specify the second derivative in an equation, use
D2y
. For example, to find the interval(s) where the function is concave down, enter
D2y < 0
in the field labeled
Enter equation to be solved (use y, Dy, D2y)
.
DerivativePlot
[
Maplet Viewer][
MapleNet]
The
DerivativePlot
maplet requires no additional discussionn except to say that the second derivative will be included in the plot if
2
is in the
orders
field.
Example 5:
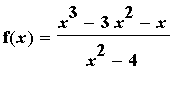
Find the intervals on which the function
| > |
f5 := (x^3-3*x^2-x)/(x^2-4):
f(x) = f5;
|
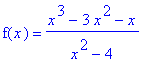
is concave up and concave down; identify any inflection points.
This is the same function as in Example 2. Recall that the domain of this function is all real numbers except
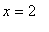 and
and
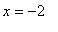 . The first two derivatives are
. The first two derivatives are
| > |
df5 := simplify( diff( f5, x ) ):
ddf5 := simplify( diff( f5, x,x ) ):
`f '`(x) = df5;
`f ''`(x) = ddf5;
|
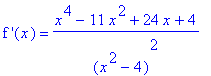
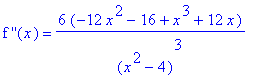
These functions are clearly defined and continuous on the domain of f, i.e., all real numbers
 except
except
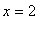 and
and
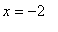 . Because the function is discontinuous at these singularities, it is possible for the concavity to change at these points. These points will be endpoints for intervals where the second derivative does not change sign.
. Because the function is discontinuous at these singularities, it is possible for the concavity to change at these points. These points will be endpoints for intervals where the second derivative does not change sign.
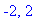
Of the three zeroes of the numerator, there is only one real-valued solution. This is the only possible inflection point.
| > |
q1 := solve( numer(ddf5) = 0, x ):
possinfl5 := op(remove( has, [q1], I )):
possinfl5 = evalf[4]( possinfl5 );
|
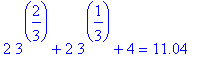
The second derivative can change sign at a point where the second derivative is zero (a possible inflection point) or where the function and/or its second derivative is not defined (a singular point). Thus, the real line is divided into the following four intervals on which the function does not change concavity:
(
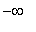 , -2 ), ( -2, 2 ), ( 2, 11.04 ), ( 11.04,
, -2 ), ( -2, 2 ), ( 2, 11.04 ), ( 11.04,
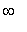 )
)
To determine on which of these intervals the function is increasing and on which it is decreasing, simply evaluate the derivative at a convenient point in each subinterval.
| > |
testpts5 := [ -3, 0, 3, 12 ]:
TestConcavity( ddf5, testpts5 );
|
f''(-3.)=-8.976; the function is concave down on the subinterval containing -3.
f''(0.)=1.500; the function is concave up on the subinterval containing 0.
f''(3.)=-2.928; the function is concave down on the subinterval containing 3.
f''(12.)=.2799e-3; the function is concave up on the subinterval containing 12.
Thus, the function
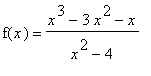 is concave up on ( -2, 2 ) and ( 11.04,
is concave up on ( -2, 2 ) and ( 11.04,
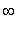 ) and concave down on (
) and concave down on (
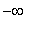 , -2 ) and ( 2, 11.04 ). Because an inflection point must, by definition, occur at a point in the domain of the function, this function has only one inflection point, at
, -2 ) and ( 2, 11.04 ). Because an inflection point must, by definition, occur at a point in the domain of the function, this function has only one inflection point, at
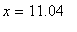 .
.
Note
Using the
solve
command, the function is found to be concave up on

and concave down on

To conclude, the graph of this function with the concave up intervals shown in pink and the concave down intervals shown in cyan confirms these results.
| > |
p1 := plot( f5, x=-5 ..-2, color=cyan,
legend=["y = f(x): concave down"] ):
p2 := plot( f5, x=-2 ..2, color=pink,
legend=["y = f(x): concave up"] ):
p3 := plot( f5, x= 2 ..11.04, color=cyan,
legend=["y = f(x): concave down"] ):
p4 := plot( f5, x=11.04..16, color=pink,
legend=["y = f(x): concave up"] ):
p5 := plot( ddf5, x=-6 ..26, color=turquoise,
discont=true, legend=["y = f ''(x)"] ):
display( [p1,p2,p3,p4,p5], view=[-6..16,-30..30] );
|
![[Maple Plot]](images/LocalAnalysis165.gif)
This plot is not as clear as might have been expected. On this scale, it is impossible to see that there actually is an inflection point. Let's take a closer look at the second derivative.
| > |
plot( ddf5, x=10..20 );
|
![[Maple Plot]](images/LocalAnalysis166.gif)
Note the scale on the vertical axis. This restores confidence in our analysis!
Example 6:
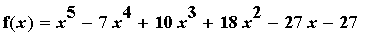
Find the intervals on which the function
| > |
f6 := x^5-7*x^4+10*x^3+18*x^2-27*x-27:
f(x) = f6;
|
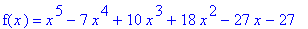
is concave up and concave down; identify all inflection points.
There are no singularities; only the possible inflection points need to be found. The second derivative is the third-degree polynomial
| > |
ddf6 := diff( f6, x,x ):
`f''`(x) = ddf6;
|
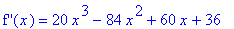
The zeroes of which are
| > |
possinfl6 := solve( ddf6 = 0, x ):
possinfl6;
evalf[4](possinfl6);
|
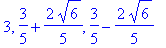
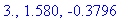
Because the derivative is continuous, the
Intermediate Value Theorem allows us to conclude that the second derivative will have one sign on each of the following four intervals:
(
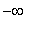 , -0.38 ), ( -0.38, 1.58 ), ( 1.58, 3 ), and ( 3,
, -0.38 ), ( -0.38, 1.58 ), ( 1.58, 3 ), and ( 3,
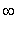 ).
).
To determine on which of these intervals the function is concave up and on which it is concave down, simply evaluate the second derivative at a convenient point in each subinterval.
| > |
testpts6 := [ -1, 0, 2, 4 ]:
TestConcavity( ddf6, testpts6 );
|
f''(-1.)=-128.; the function is concave down on the subinterval containing -1.
f''(0.)=36.; the function is concave up on the subinterval containing 0.
f''(2.)=-20.; the function is concave down on the subinterval containing 2.
f''(4.)=212.; the function is concave up on the subinterval containing 4.
Thus, the function
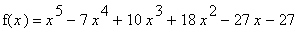 is concave up on ( -0.38, 1.58 ) and ( 3,
is concave up on ( -0.38, 1.58 ) and ( 3,
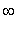 ) and concave down on (
) and concave down on (
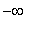 , -0.38 ) and ( 1.58, 3 ). The three inflection points for this function: occur at
, -0.38 ) and ( 1.58, 3 ). The three inflection points for this function: occur at
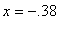 ,
,
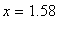 , and
, and
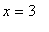 .
.
Note
Using the
solve
command, the function is found to be increasing on
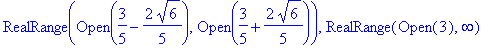
and decreasing on

To conclude, the graph of this function with the concave up intervals shown in pink and the concave down intervals shown in cyan confirms these results.
| > |
p1 := plot( f6, x=-2 ..-0.38, color=cyan, legend=["y = f(x): concave down"] ):
p2 := plot( f6, x=-0.38.. 1.58, color=pink, legend=["y = f(x): concave up"] ):
p3 := plot( f6, x= 1.58.. 3, color=cyan, legend=["y = f(x): concave down"] ):
p4 := plot( f6, x= 3 .. 5, color=pink, legend=["y = f(x): concave up"] ):
p5 := plot( ddf6, x=-3..5, color=turquoise, legend=["y = f ''(x)"] ):
display( [p1,p2,p3,p4,p5], view=[-2..5,-100..200] );
|
![[Maple Plot]](images/LocalAnalysis182.gif)
The three inflection points are clearly visible in this plot. It should also be noted that the
 = 3 is both an inflection point and a stationary point.
= 3 is both an inflection point and a stationary point.
Point 3: Locating and Classifying Local Extrema
To conclude this lesson there are two tests for locating and classifying local extrema. For example, if a function with a continuous derivative has a local maximum at a point then the function must be increasing to the left and decreasing to the right of the local maximum. That is, at the critical point the first derivative is zero and changes sign from positive to negative. Moreover, since the first derivative changes from positive to negative, the first derivative is decreasing. This means the second derivative is negative and so the function is concave down. These observations combined with the analogous statements for a local minimum are summarized in the First and Second Derivative Tests.
Theorem: First Derivative Test
Suppose
-
f is a function that is differentiable on an interval
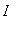 and
and
-
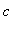 is a critical point of f in
is a critical point of f in
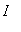 .
.
Then,
-
if
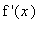 changes sign from negative to positive at
changes sign from negative to positive at
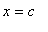 , then f has a local maximum at
, then f has a local maximum at
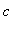
-
if
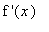 changes sign from positive to negative at
changes sign from positive to negative at
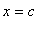 , then f has a local minimum at
, then f has a local minimum at
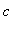
Notes:
-
If
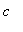 is a critical point of f but the derivative does not change sign at
is a critical point of f but the derivative does not change sign at
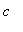 , then
, then
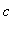 is neither a local maximum nor a local minimum.
is neither a local maximum nor a local minimum.
-
Technically, the derivative does not need to exist at
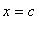 , but it is essential that the function be continuous at
, but it is essential that the function be continuous at
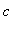 .
.
-
For example, if f has a corner or a cusp, then
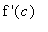 will not exist but the derivative is likely to exists on either side of
will not exist but the derivative is likely to exists on either side of
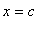 . The theorem does apply to this situation, assuming the first derivative changes sign at
. The theorem does apply to this situation, assuming the first derivative changes sign at
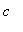 .
.
Theorem: Second Derivative Test
Suppose
-
f is a function with a second derivative on an interval
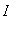 and
and
-
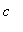 is a point in
is a point in
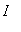 with
with
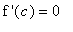 .
.
Then,
-
if
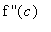 < 0, then f has a local maximum at
< 0, then f has a local maximum at
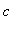
-
if
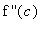 > 0, then f has a local minimum at
> 0, then f has a local minimum at
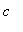
Notes:
-
Points where
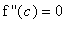 are
possible
inflection points. Recall that it is necessary to check for the sign change in f '' at this point.
are
possible
inflection points. Recall that it is necessary to check for the sign change in f '' at this point.
-
The first hypothesis implies f is continuous on I (in particular, at c); this theorem does not apply at a discontinuity of f.
-
The second hypothesis implies that the theorem applies only at points where f has a horizontal tangent. If
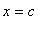 is a singularity of f then the theorem does not apply.
is a singularity of f then the theorem does not apply.
Example 7:
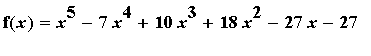
Find the intervals on which the function
| > |
f7 := x^5-7*x^4+10*x^3+18*x^2-27*x-27:
f(x) = f7;
|
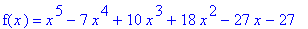
is increasing, decreasing, concave up and concave down; identify all local extrema and all inflection points.
This is the third time this function has appeared in this lesson. The analysis based on the first derivative was essentially completed in Example 3:
The first derivative is
| > |
df7 := diff( f7, x ):
`f '`(x) = df7;
|
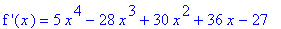
and the (four) stationary points are
| > |
stat7 := solve( df7 = 0, x ):
stat7;
|
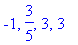
The derivative will have one sign on each of the following four intervals:
(
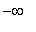 , -1 ), ( -1,
, -1 ), ( -1,
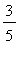 ), (
), (
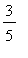 , 3 ), and ( 3,
, 3 ), and ( 3,
 ).
).
Testing the sign of the derivative at one point in each of these intervals yields:
| > |
testpts7a := [ -2, 0, 2, 4 ]:
TestIncrDecr( df7, testpts7a );
|
f'(-2.)=325.; the function is increasing on the subinterval containing -2.
f'(0.)=-27.; the function is decreasing on the subinterval containing 0.
f'(2.)=21.; the function is increasing on the subinterval containing 2.
f'(4.)=85.; the function is increasing on the subinterval containing 4.
Based on this information we concluded the function
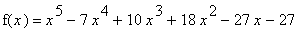 is increasing on (
is increasing on (
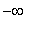 , -1 ), (
, -1 ), (
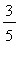 ,
,
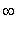 ) and decreasing on ( -1,
) and decreasing on ( -1,
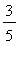 ). Further, the First Derivative Test allows us to conclude the function has a local maximum at
). Further, the First Derivative Test allows us to conclude the function has a local maximum at
 = -1 and a local minimum at
= -1 and a local minimum at
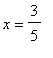 . The critical point at
. The critical point at
 = 3 is neither a local maximum nor a local minimum because the first derivative is positive on both sides of
= 3 is neither a local maximum nor a local minimum because the first derivative is positive on both sides of
 = 3.
= 3.
The analysis based on the second derivative was started in Example 6:
The second derivative is the third-degree polynomial
| > |
ddf7 := diff( f7, x,x ):
`f ''`(x) = ddf7;
|
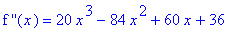
The zeroes of which are
| > |
possinfl7 := solve( ddf7 = 0, x ):
possinfl7;
evalf[7](possinfl7);
|
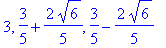
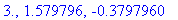
The second derivative has one sign on each of the following four intervals:
(
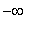 , -0.38 ), ( -0.38, 1.58 ), ( 1.58, 3 ), and ( 3,
, -0.38 ), ( -0.38, 1.58 ), ( 1.58, 3 ), and ( 3,
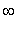 ).
).
Concavity is determined by evaluating the second derivative at a convenient point in each subinterval.
| > |
testpts7b := [ -1, 0, 2, 4 ]:
TestConcavity( ddf7, testpts7b );
|
f''(-1.)=-128.; the function is concave down on the subinterval containing -1.
f''(0.)=36.; the function is concave up on the subinterval containing 0.
f''(2.)=-20.; the function is concave down on the subinterval containing 2.
f''(4.)=212.; the function is concave up on the subinterval containing 4.
Thus, the function
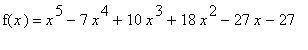 is concave up on ( -0.38, 1.58 ) and ( 3,
is concave up on ( -0.38, 1.58 ) and ( 3,
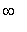 ) and concave down on (
) and concave down on (
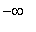 , -0.38 ) and ( 1.58, 3 ). The three inflection points for this function occur at
, -0.38 ) and ( 1.58, 3 ). The three inflection points for this function occur at
 = 0.38,
= 0.38,
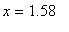 , and
, and
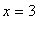 .
.
To use the Second Derivative Test to classify the critical points it suffices to determine the concavity at each stationary point.
| > |
TestConcavity( ddf7, {stat7} );
|
f''(3.)=0.; the function has a possible inflection point at x = 3.
f''(-1.)=-128.; the function is concave down on the subinterval containing -1.
f''(.6000)=46.08; the function is concave up on the subinterval containing .6000
Thus, this function has a local maximum at
 = -1, a local minimum at
= -1, a local minimum at
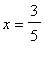 , and
, and
 = 3 is not a local extremum. These results are consistent with those found with the First Derivative Test.
= 3 is not a local extremum. These results are consistent with those found with the First Derivative Test.
| > |
FunctionChart( f7, -7/4..4,
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/LocalAnalysis256.gif)
All zeroes of the function are identified with a circle, all stationary points are marked with diamonds, and inflection points with a cross; the curve is plotted in red on intervals where the function is increasing and in blue where the function is decreasing; the pink shaded regions are the regions under the curve when the function is concave up and the cyan regions are the regions under the curve when the function is concave down.
The appearance of a circle, diamond, and cross at
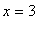 reinforces the earlier observation that this point is a stationary point and a critical point (not to mention a zero) for this function. Algebraically, this means
reinforces the earlier observation that this point is a stationary point and a critical point (not to mention a zero) for this function. Algebraically, this means
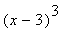 must be a factor of this function; the fact that
must be a factor of this function; the fact that
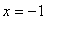 is a zero and stationary point of the function means
is a zero and stationary point of the function means
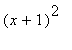 must be a factor of the polynomial. Because the original polynomial is fifth degrree, it must be the case that
must be a factor of the polynomial. Because the original polynomial is fifth degrree, it must be the case that
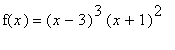
| > |
f(x) = f7;
`` = factor( f7 );
|
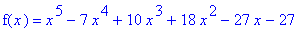
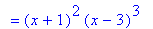
Maplets for Local Analysis
The full power of the three maplets introduced earlier in the lesson can now be realized.
CurveAnalysis
[
Maplet Viewer][
MapleNet]
The
CurveAnalysis
maplet can
Show
or
Plot
the function, local maxima and minima, intervals on which the function is increasing and decreasing, and intervals where the function is concave up and concave down.
FunctionAnalyzer
[
Maplet Viewer][
MapleNet]
The
FunctionAnalyzer
maplet is an excellent tool to help work through the local analysis of a function. Its interface allows the user to specify the relevant equations to be solved to determine stationary points, possible inflection points, intervals on which the function is increasing/decreasing/concave up/concave down, etc.. The plot window can display any combination of the function, its first two derivatives, and the sign charts for the first and second derivative.
Note that this maplet can be used if you need to perform some analysis on a function for which only the first (or second) derivative is known.
DerivativePlot
[
Maplet Viewer][
MapleNet]
The
DerivativePlot
maplet is much simpler; all it can do is display a plot of any combination of the function and its derivatives.
Example 8:
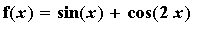
Consider the trigonometric function from Example 8 in the
GlobalAnalysis lesson.
| > |
f8 := sin(x)+cos(2*x):
f(x) = f8;
|
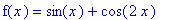
Identify the subintervals of one period of this function on which this function is increasing, decreasing, concave up, and concave down. Also, find the local extrema and inflection points.
The period of this function is
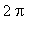 . It suffices to complete the local analysis on [
. It suffices to complete the local analysis on [
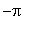 ,
,
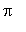 ]; the behavior of the function for the rest of the real line is obtained by shifting. This function, and all its derivatives, are continous; there are no singularities. The possible locations for inflection points are the zeroes of the second derivative:
]; the behavior of the function for the rest of the real line is obtained by shifting. This function, and all its derivatives, are continous; there are no singularities. The possible locations for inflection points are the zeroes of the second derivative:
| > |
df8 := collect(diff( f8, x ),[sin,cos]):
ddf8 := collect(diff( f8, x,x ),[sin,cos]):
`f '`(x) = df8;
`f ''`(x) = ddf8;
|
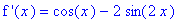
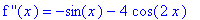
On the closed and bounded interval [
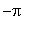 ,
,
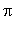 ] the critical points consist of the stationary points
] the critical points consist of the stationary points
| > |
q1 := df8 = 0:
stat8 := solve( q1, x ):
stat8;
|
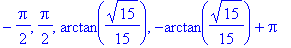
and the endpoints of one period of the function
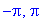
| > |
crit8 := stat8, end8:
crit8;
evalf[4]( crit8 );
|

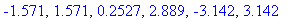
The derivative has a constant sign on each of the following intervals:
[ -3.142, -1.571 ), ( -1.571, 0.253 ), ( 0.253, 1.571 ), ( 1.571, 2.889 ), ( 2;889, 3.142 ]
| > |
testpts8a := [ -2, 0, 1, 2, 3 ]:
TestIncrDecr( df8, testpts8a );
|
f'(-2.)=-1.930; the function is decreasing on the subinterval containing -2.
f'(0.)=1.; the function is increasing on the subinterval containing 0.
f'(1.)=-1.279; the function is decreasing on the subinterval containing 1.
f'(2.)=1.098; the function is increasing on the subinterval containing 2.
f'(3.)=-.4312; the function is decreasing on the subinterval containing 3.
Thus, f is increasing on ( -1.571, 0.253 ), ( 1.571, 2.889 ) and decreasing on [ -3.142, -1.571 ), ( 0.253, 1.571 ), ( 2;889, 3.142 ]. Moreover, by the First Derivative Test, f has local maxima at
 = 0.253 and
= 0.253 and
 = 2.889 and local minima at
= 2.889 and local minima at
 = -1.571 and
= -1.571 and
 = 1.571 (and at all points obtained by adding an integer multiple of
= 1.571 (and at all points obtained by adding an integer multiple of
 to these positions).
to these positions).
The possible inflection points in [
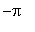 ,
,
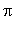 ] are the zeroes of the second derivative:
] are the zeroes of the second derivative:
| > |
q2 := ddf8 = 0:
possinfl8 := solve( q2, x ):
possinfl8;
evalf[4]( possinfl8 );
|
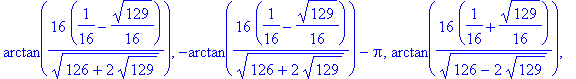
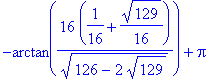
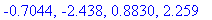
The second derivative does not change sign on each of the intervals:
[ -3.142, -2.438 ), ( -2.438, -0.7044 ), ( -0.7044, 0.8830 ), ( 0.8830, 2.259 ), ( 2.259, 3.142 ].
| > |
testpts8b := [ -3, -1, 0, 1, 3 ]:
TestConcavity( ddf8, testpts8b );
|
f''(-3.)=-3.700; the function is concave down on the subinterval containing -3.
f''(-1.)=2.506; the function is concave up on the subinterval containing -1.
f''(0.)=-4.; the function is concave down on the subinterval containing 0.
f''(1.)=.8225; the function is concave up on the subinterval containing 1.
f''(3.)=-3.982; the function is concave down on the subinterval containing 3.
Thus, f is concave up on ( -2.438, -0.7044 ) and ( 0.8830, 2.259 ) and concave down on [ -3.142, -2.438 ), ( -0.7044, 0.8830 ), and ( 2.259, 3.142 ]. The change in concavity at each possible inflection point means there are four inflection points in [
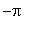 ,
,
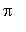 ]:
]:
 = -2.438,
= -2.438,
 = -0.7044,
= -0.7044,
 = 0.8830, and
= 0.8830, and
 = 2.259.
= 2.259.
To classify the stationary points using the Second Derivative Test it is necessary to evaluate the second derivative at each stationary point:
| > |
TestConcavity( ddf8, [stat8] );
|
f''(-1.571)=5.000; the function is concave up on the subinterval containing -1.571
f''(1.571)=3.000; the function is concave up on the subinterval containing 1.571
f''(.2527)=-3.750; the function is concave down on the subinterval containing .2527
f''(2.889)=-3.750; the function is concave down on the subinterval containing 2.889
Because the second derivative is positive at
 = -1.571 and
= -1.571 and
 = 1.571, f has local minima at these points. Similarly, the function has local maxima at
= 1.571, f has local minima at these points. Similarly, the function has local maxima at
 = 0.253 and
= 0.253 and
 = 2.889 because the second derivative is positive at these points. (Note that this is the same conclusion reached with the First Derivative Test.)
= 2.889 because the second derivative is positive at these points. (Note that this is the same conclusion reached with the First Derivative Test.)
Instead of piecing together plots as in earlier examples, the
FunctionChart
command from the
Student[Calculus1]
package will be used to create a single plot displaying the results of our local analysis.
| > |
FunctionChart( f8, -Pi..Pi,
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/LocalAnalysis297.gif)
In this picture, all zeroes of the function are identified with a circle, all stationary points are marked with diamonds, and inflection points with a cross; the curve is plotted in red on intervals where the function is increasing and in blue where the function is decreasing; the pink shaded regions are the regions under the curve when the function is concave up and the cyan regions are the regions under the curve when the function is concave down. This picture confirms all of the results obtained directly analytically.
Example 9:
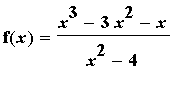
Consider the function
| > |
f8 := (x^3-3*x^2-x)/(x^2-4):
f(x) = f8;
|
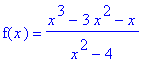
Find all intervals where this function is increasing, decreasing, concave up, and concave down. In addition, identify all local and global extrema and inflection points.
This function has been analyzed in Examples 2 and 5. The stationary points are the real-valued zeroes of the first derivative
| > |
df8 := simplify( diff( f8, x ) ):
`f '`(x) = df8:
q1 := solve( numer(df5)=0, x ):
stat8 := op(remove( has, evalf[4](allvalues([q1])), I )):
stat8;
|
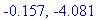
The function has two singularities
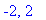
Thus, the critical points are
| > |
crit8 := stat8, sing8:
crit8;
|
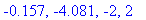
The sign of the first derivative does not change on the intervals defined by these points:
(
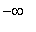 , -4.08 ), ( -4.08, -2 ), ( -2, -0.16 ), ( -0.16, 2 ), ( 2,
, -4.08 ), ( -4.08, -2 ), ( -2, -0.16 ), ( -0.16, 2 ), ( 2,
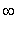 )
)
Testing the sign of the first derivative at a convenient point in each of these intervals:
| > |
testpts8a := [ -5, -3, -1, 1, 3 ]:
TestIncrDecr( df8, testpts8a );
|
f'(-5.)=.5306; the function is increasing on the subinterval containing -5.
f'(-3.)=-3.440; the function is decreasing on the subinterval containing -3.
f'(-1.)=-3.333; the function is decreasing on the subinterval containing -1.
f'(1.)=2.000; the function is increasing on the subinterval containing 1.
f'(3.)=2.320; the function is increasing on the subinterval containing 3.
Thus, the function
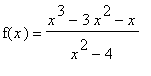 is increasing on (
is increasing on (
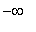 , -4.081 ), ( -0.157, 2 ), and ( 2,
, -4.081 ), ( -0.157, 2 ), and ( 2,
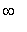 ) and decreasing on ( -4.081, -2 ) and ( -2, -0.157 ). The First Derivative Test classifies
) and decreasing on ( -4.081, -2 ) and ( -2, -0.157 ). The First Derivative Test classifies
 = -4.081 as a local maximum and
= -4.081 as a local maximum and
 = -0.157 as a local minimum. The First Derivative Test does not apply at the two singularities because the function is not continuous at these points. (In fact, the graph of the function has vertical asymptotes at
= -0.157 as a local minimum. The First Derivative Test does not apply at the two singularities because the function is not continuous at these points. (In fact, the graph of the function has vertical asymptotes at
 = -2 and
= -2 and
 = 2.)
= 2.)
For the analysis based on the second derivative:
| > |
ddf8 := simplify( diff( f8, x,x ) ):
`f ''`(x) = ddf8;
|
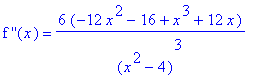
The possible inflection points are the real-valued zeroes of the numerator:
| > |
q1 := solve( numer(ddf5) = 0, x ):
possinfl5 := op(remove( has, [q1], I )):
possinfl5;evalf[4]( possinfl5 );
|
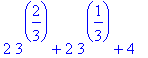
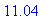
This possible inflection point and the two singularities of the function define four intervals on which the second derivative cannot change sign:
(
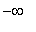 , -2 ), ( -2, 2 ), ( 2, 11.04 ), ( 11.04,
, -2 ), ( -2, 2 ), ( 2, 11.04 ), ( 11.04,
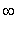 )
)
To determine the convexity on each interval, evaluate the second derivative at a convenient point in each subinterval:
| > |
testpts8 := [ -3, 0, 3, 12 ]:
TestConcavity( ddf8, testpts8 );
|
f''(-3.)=-8.976; the function is concave down on the subinterval containing -3.
f''(0.)=1.500; the function is concave up on the subinterval containing 0.
f''(3.)=-2.928; the function is concave down on the subinterval containing 3.
f''(12.)=.2799e-3; the function is concave up on the subinterval containing 12.
Thus, the function
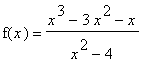 is concave up on ( -2, 2 ) and ( 11.04,
is concave up on ( -2, 2 ) and ( 11.04,
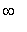 ) and concave down on (
) and concave down on (
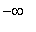 , -2 ) and ( 2, 11.04 ). The only inflection point for this function occurs at
, -2 ) and ( 2, 11.04 ). The only inflection point for this function occurs at
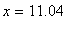 .
.
To classify the stationary points using the Second Derivative Test it is necessary to determine the concavity of the function at each stationary point:
| > |
TestConcavity( ddf8, [stat8] );
|
f''(-.157)=1.736; the function is concave up on the subinterval containing -.157
f''(-4.081)=-.9864; the function is concave down on the subinterval containing -4.081
Thus,
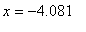 is a local maximum and
is a local maximum and
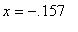 is a local minimum for this function. (The Second Derivative Test tells us nothing about the singularities.)
is a local minimum for this function. (The Second Derivative Test tells us nothing about the singularities.)
This information is consistent with the plots created previously and here, using the
FunctionChart
command.
| > |
FunctionChart( f8, -10..16, view=[DEFAULT,-20..20],
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/LocalAnalysis323.gif)
Example 10:
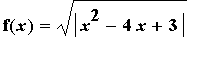
Let
| > |
f10 := sqrt( abs(x^2-4*x+3) ):
f(x) = f10;
|
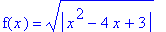
Find all intervals where this function is increasing, decreasing, concave up, and concave down. In addition, identify all local and global extrema and inflection points.
This function was first encountered in Example 10 of the
Global Analysis lesson. Recall that this function is defined for all real numbers. The first derivative is
| > |
df10 := simplify(diff( f10, x )):
`f'`(x) = convert(df10,piecewise,x);
|
![`f'`(x) = PIECEWISE([(x-2)/(x^2-4*x+3)^(1/2), x < 1],[undefined, x = 1],[-(x-2)/(-3-x^2+4*x)^(1/2), x < 3],[undefined, x = 3],[(x-2)/(x^2-4*x+3)^(1/2), 3 < x])](images/LocalAnalysis326.gif)
There are two singularities
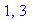
and the sole stationary point is
| > |
q1 := df10 = 0:
stat10 := solve( q1, x ):
stat10;
|
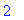
The full set of critical points for this function is
| > |
crit10 := [ sing10, stat10 ]:
crit10;
|
![[1, 3, 2]](images/LocalAnalysis329.gif)
The first derivative does not change sign on the intervals
(
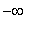 , 1 ), ( 1, 2 ), ( 2, 3 ), and ( 3,
, 1 ), ( 1, 2 ), ( 2, 3 ), and ( 3,
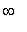 )
)
Evaluation of the first derivative at a single point in each interval shows:
| > |
testpts10a := [ 0, 3/2, 5/2, 4 ]:
TestIncrDecr( df10, testpts10a );
|
f'(0.)=-1.155; the function is decreasing on the subinterval containing 0.
f'(1.500)=.5775; the function is increasing on the subinterval containing 1.500
f'(2.500)=-.5775; the function is decreasing on the subinterval containing 2.500
f'(4.)=1.155; the function is increasing on the subinterval containing 4.
Thus, the function is increasing on ( 1, 2 ) and ( 3,
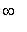 ) and decreasing on (
) and decreasing on (
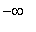 , 1 ) and ( 2, 3 ). Further, the First Derivative Test can be applied at each critical point (yes, including the singular points) to conclude that the function has a local maximum at
, 1 ) and ( 2, 3 ). Further, the First Derivative Test can be applied at each critical point (yes, including the singular points) to conclude that the function has a local maximum at
 = 2 and local minima at
= 2 and local minima at
 = 1 and
= 1 and
 = 3.
= 3.
The second derivative is
| > |
ddf10 := simplify( diff( f10, x,x ) ):
`f ''`(x) = convert( ddf10, piecewise, x );
|
![`f ''`(x) = PIECEWISE([-1/((x^2-4*x+3)^(3/2)), x < 1],[undefined, x = 1],[-1/((-3-x^2+4*x)^(3/2)), x < 3],[undefined, x = 3],[-1/((x^2-4*x+3)^(3/2)), 3 < x])](images/LocalAnalysis337.gif)
There are no possible inflection points
| > |
q2 := ddf10=0:
possinfl10 := solve( q2, x ):
possinfl10;
|
The representation of the second derivative shown above clearly indicates that the second derivative will be negative everywhere it is defined. If this is not seen, the singular points separate the real line into three subintervals on which the second derivative does not change sign:
(
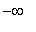 , 1 ), ( 1, 3 ), and ( 3,
, 1 ), ( 1, 3 ), and ( 3,
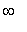 )
)
| > |
testpts10b := [ 0, 2, 4 ]:
TestConcavity( ddf10, testpts10b );
|
f''(0.)=-.1925; the function is concave down on the subinterval containing 0.
f''(2.)=-1.; the function is concave down on the subinterval containing 2.
f''(4.)=-.1925; the function is concave down on the subinterval containing 4.
and the function is concave down for all real numbers except
 = 1 and
= 1 and
 = 3.
= 3.
Because
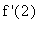 = 0 and
= 0 and
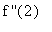 < 0, the Second Derivative Test implies
< 0, the Second Derivative Test implies
 = 2 is a local maximum. Note that the Second Derivative Test cannot be used to classify the singular points,
= 2 is a local maximum. Note that the Second Derivative Test cannot be used to classify the singular points,
 = 1 and
= 1 and
 = 3.
= 3.
These results are all summarized in the plot
| > |
FunctionChart( f10, -2..6,
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/LocalAnalysis347.gif)
Example 11:
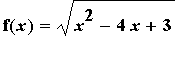
Define
| > |
f11 := sqrt( x^2-4*x+3 ):
f(x) = f11;
|
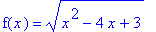
Find all intervals where this function is increasing, decreasing, concave up, and concave down. In addition, identify all local and global extrema and inflection points.
This function is similar to the one just studied in Example 10. The first impact of the removal of the absolute value is that the domain of the function is the union of the (closed) sets (
 , 1 ] and [ 3,
, 1 ] and [ 3,
 ).
).
The first derivative is
| > |
df11 := simplify(diff( f11, x )):
`f '`(x) = df11;
|
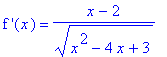
The lone zero of the first derivative is
| > |
q1 := solve( numer(df11) = 0, x ):
q1;
|
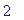
but note that this point is not in the domain of f. Thus, there are no stationary points:
| > |
stat11 := remove( InInterval, q1, [1,3] ):
stat11;
|
Because
 = 1 and
= 1 and
 = 3 are points in the domain of the function but where the first derivative is not defined, we have two singular points:
= 3 are points in the domain of the function but where the first derivative is not defined, we have two singular points:
| > |
sing11 := 1, 3:
sing11;
|
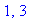
The complete set of critical points is
| > |
crit11 := [ stat11, sing11 ]:
crit11;
|
![[1, 3]](images/LocalAnalysis357.gif)
Because there are no other stationary points, the first derivative will be not change sign on either of the intervals
(
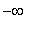 , 1 ) and ( 3,
, 1 ) and ( 3,
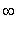 )
)
When the first derivative is evaluated at a convenient point in each interval it is found that
| > |
testpts11a := [ -2, 4 ]:
TestIncrDecr( df11, testpts11a );
|
f'(-2.)=-1.033; the function is decreasing on the subinterval containing -2.
f'(4.)=1.155; the function is increasing on the subinterval containing 4.
The function is increasing on ( 3,
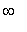 ) and is decreasing on (
) and is decreasing on (
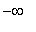 , 1 ). While the First Derivative Test is not applicable at the singular points (because the first derivative is not defined on both sides of the point), the definition of a local minimum and the fact that the function decreases for all
, 1 ). While the First Derivative Test is not applicable at the singular points (because the first derivative is not defined on both sides of the point), the definition of a local minimum and the fact that the function decreases for all
 < 1 are sufficient to allow us to conclude
< 1 are sufficient to allow us to conclude
 = 1 is a local minimum. Likewise, the observation that the function is increasing for all
= 1 is a local minimum. Likewise, the observation that the function is increasing for all
 > 3 means
> 3 means
 = 3 is also a local minimum of the function.
= 3 is also a local minimum of the function.
The second derivative is
| > |
ddf11 := simplify( diff( f11, x,x ) ):
`f ''`(x) = ddf11;
|
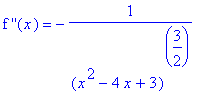
Thie second derivative is defined, and negative, for all
 < 1 or
< 1 or
 > 3. Thus, the function is concave down on its domain and has no inflection points. Because there are no stationary points, the Second Derivative Test is of no use for this function.
> 3. Thus, the function is concave down on its domain and has no inflection points. Because there are no stationary points, the Second Derivative Test is of no use for this function.
Thus,
 = -4.081 is a local maximum and
= -4.081 is a local maximum and
 = -0.157 is a local minimum for this function. (The Second Derivative Test tells us nothing about the singularities.)
= -0.157 is a local minimum for this function. (The Second Derivative Test tells us nothing about the singularities.)
This information is consistent with the plots created previously and here, using the
FunctionChart
command.
| > |
FunctionChart( f11, -2..6,
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/LocalAnalysis371.gif)
![]() .
.
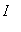 if the function values become larger as the independent variable becomes larger,
if the function values become larger as the independent variable becomes larger,![x[1]](images/LocalAnalysis3.gif) and
and
![x[2]](images/LocalAnalysis4.gif) in
in
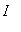 with
with
![x[1]](images/LocalAnalysis6.gif) <
<
![x[2]](images/LocalAnalysis7.gif) , it is true that
, it is true that
![f(x[1])](images/LocalAnalysis8.gif) <
<
![f(x[2])](images/LocalAnalysis9.gif) ;
;
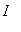 if the function values become smaller as the independent variable becomes larger,
if the function values become smaller as the independent variable becomes larger,![x[1]](images/LocalAnalysis11.gif) and
and
![x[2]](images/LocalAnalysis12.gif) in
in
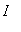 with
with
![x[1]](images/LocalAnalysis14.gif) <
<
![x[2]](images/LocalAnalysis15.gif) , it is true that
, it is true that
![f(x[1])](images/LocalAnalysis16.gif) >
>
![f(x[2])](images/LocalAnalysis17.gif) .
.
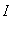 is neither increasing nor decreasing.
is neither increasing nor decreasing.
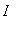 when
when
![x[1]](images/LocalAnalysis20.gif) <
<
![x[2]](images/LocalAnalysis21.gif) implies
implies
![f(x[1])](images/LocalAnalysis22.gif) <=
<=
![f(x[2])](images/LocalAnalysis23.gif) .
.
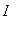 when
when
![x[1]](images/LocalAnalysis25.gif) <
<
![x[2]](images/LocalAnalysis26.gif) implies
implies
![f(x[1])](images/LocalAnalysis27.gif) >=
>=
![f(x[2])](images/LocalAnalysis28.gif) .
.
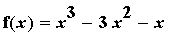
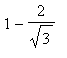 ), (
), (
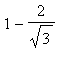 ,
,
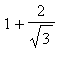 ), and (
), and (
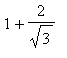 ,
,
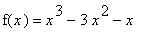 is increasing on (
is increasing on (
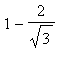 ) and (
) and (
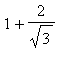 ,
,
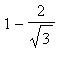 ,
,
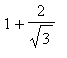 ).
).
![[Maple Plot]](images/LocalAnalysis64.gif)
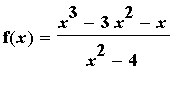
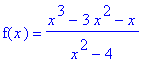
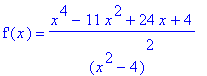
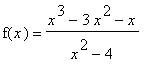 is increasing on (
is increasing on (
![[Maple Plot]](images/LocalAnalysis86.gif)
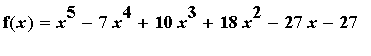
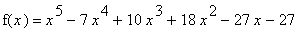 is increasing on (
is increasing on (
![[Maple Plot]](images/LocalAnalysis108.gif)
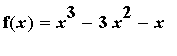
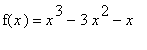 is concave up on ( 1,
is concave up on ( 1,
![[Maple Plot]](images/LocalAnalysis144.gif)
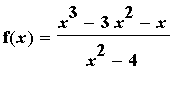
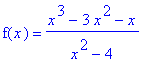
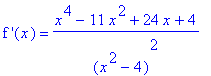
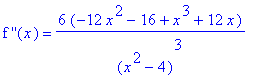
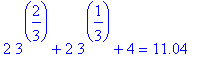
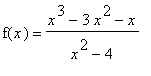 is concave up on ( -2, 2 ) and ( 11.04,
is concave up on ( -2, 2 ) and ( 11.04,


![[Maple Plot]](images/LocalAnalysis165.gif)
![[Maple Plot]](images/LocalAnalysis166.gif)
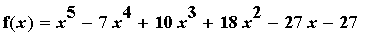
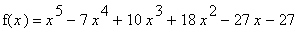 is concave up on ( -0.38, 1.58 ) and ( 3,
is concave up on ( -0.38, 1.58 ) and ( 3,
![[Maple Plot]](images/LocalAnalysis182.gif)
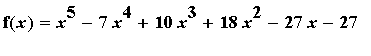
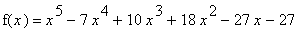 is increasing on (
is increasing on (
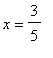 . The critical point at
. The critical point at
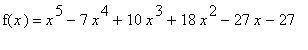 is concave up on ( -0.38, 1.58 ) and ( 3,
is concave up on ( -0.38, 1.58 ) and ( 3,
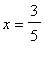 , and
, and
![[Maple Plot]](images/LocalAnalysis256.gif)
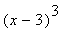 must be a factor of this function; the fact that
must be a factor of this function; the fact that
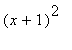 must be a factor of the polynomial. Because the original polynomial is fifth degrree, it must be the case that
must be a factor of the polynomial. Because the original polynomial is fifth degrree, it must be the case that
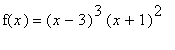
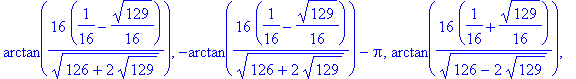
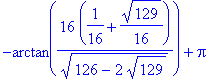
![[Maple Plot]](images/LocalAnalysis297.gif)
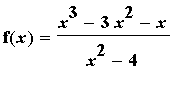
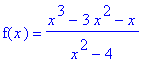
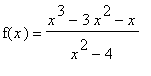 is increasing on (
is increasing on (
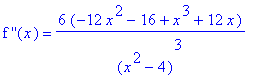
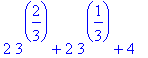
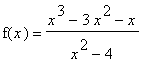 is concave up on ( -2, 2 ) and ( 11.04,
is concave up on ( -2, 2 ) and ( 11.04,
![[Maple Plot]](images/LocalAnalysis323.gif)
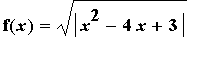
![`f'`(x) = PIECEWISE([(x-2)/(x^2-4*x+3)^(1/2), x < 1],[undefined, x = 1],[-(x-2)/(-3-x^2+4*x)^(1/2), x < 3],[undefined, x = 3],[(x-2)/(x^2-4*x+3)^(1/2), 3 < x])](images/LocalAnalysis326.gif)
![`f ''`(x) = PIECEWISE([-1/((x^2-4*x+3)^(3/2)), x < 1],[undefined, x = 1],[-1/((-3-x^2+4*x)^(3/2)), x < 3],[undefined, x = 3],[-1/((x^2-4*x+3)^(3/2)), 3 < x])](images/LocalAnalysis337.gif)
![[Maple Plot]](images/LocalAnalysis347.gif)
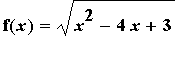
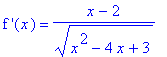
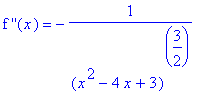
![[Maple Plot]](images/LocalAnalysis371.gif)