Lesson Overview
The
Global Analysis and
Local Analysis lessons have introduced all of the tools needed to graph almost any function that you will encounter. While the
FunctionChart
command, in the
Student[Calculus1]
package, can produce excellent graphs, the ability to graph a function by hand is important for many reasons, including:
-
some graphs have subtle properties that are difficult to completely represent graphically (Example 2)
-
most software is unable to graph functions that involve a parameter (Example 3)
-
sometimes it is necessary to construct a graph when only the first derivative is known (Example 5)
-
a computer and appropriate software are not always available
-
some knowledge about the curve is needed to be able to use the software effectively
-
creating a graph of a function is a good test of a person's understanding of differential calculus
A general approach to graphing a function will be given and then demonstrated on a varied collection of functions. Some of the functions considered in these examples are somewhat more complicated than the typical functions considered in examples and exercises. These functions have been chosen to emphasize the general techniques and approach and to let Maple do some of the tedious calculations. In support of this approach, this worksheet introduces the
SignChart
command (defined at the top of this worksheet). The general usage of this command is
SignChart( f, domain, orders );
where
f
is the expression containing the function to be analyzed,
domain
is an equation of the form
var = left .. right
where
var
is the variable in
f
and
left
and
right
are the left and right endpoints of the interval for which the sign chart is requested, and
orders
is a single integer or a list of integers indicating the order of the derivative(s) to include in the sign chart (use
0
for the f,
1
for f ', and
2
for f ''). Each sign chart is labeled and uses pink to indicate intervals where the function (or derivative) is positive and cyan to indicte regions where the function (or derivative) is negative.
Because the emphasis is on obtaining the information needed to construct the graph of a function, the
FunctionAnalyzer
maplet [
Maplet Viewer][
MapleNet] is recommended over the
CurveAnalysis
[
Maplet Viewer][
MapleNet] and
DerivativePlot
[
Maplet Viewer][
MapleNet] maplets. To display a function in a Maple worksheet, the
FunctionChart
command in the
Student[Calculus1]
package is recommended.
General Approach to Graphing a Function
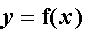
The process of creating a good graph of a function depends on the specific function to be graphed. The following list of steps can be used for most functions you are likely to encounter. Some of the steps can be omitted for some problems, but the decision to skip a step, or a part of a step, needs to be a conscious decision rather than one of omission.
Steps 1-3: Analysis Based on the Function
Step 1: Domain, Range, Symmetry, Periodicity
-
Domain
If an interval is provided, use this as the domain.
Otherwise, determine the function's natural domain.
-
Range
Attempt to determine the range of the function.
In particular, is the range bounded or unbounded?
(Sometimes this becomes clearer after completing Step 2.)
-
Periodicity
If the function is periodic, find its period.
-
Symmetry
Is the function even (symmetric about the y-axis)? odd (symmetric about the origin)?
Step 2: Intercept, Zeroes, Endpoints
-
Intercept
Determine the point ( 0,
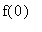 ).
).
-
Zeroes
Attempt to locate all solutions to
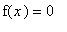 .
.
Put all points (
 , 0 ) where
, 0 ) where
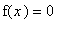 .
.
-
Endpoints
Collect information for each finite endpoint.
Note
: For an endpoint not in the domain, use an appropriate one-sided limit.
-
Sign Chart for
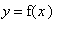
Determine intervals of the domain where the function is positive and where the function is negative.
Step 3 Asymptotes
-
Horizontal
If the domain includes
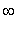 or
or
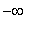 , compute the corresponding limit at infinity.
, compute the corresponding limit at infinity.
If this limit is finite, then this value is a horizontal asymptote.
E.g., if
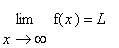 , then
, then
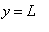 is a horizontal asymptote.
is a horizontal asymptote.
-
Vertical
For any finite number
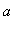 , if either one-sided limit of f at
, if either one-sided limit of f at
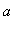 is infinite, then
is infinite, then
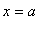 is a vertical asymptote.
is a vertical asymptote.
-
Oblique
If there are values of
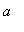 and
and
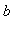 such that either
such that either
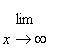
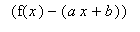 = 0 or
= 0 or
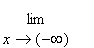
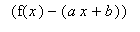 = 0,
= 0,
then
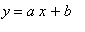 is an oblique asymptote.
is an oblique asymptote.
Note
: After computing the asymptotes, check that this information is consistent with the range found in Step 0.
Step 4: Analysis Based on the First Derivative
-
Critical Points
Find all stationary points, singular points, and endpoints.
-
Sign Chart for
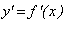
Determine the intervals of the domain where the function is increasing and where the function is decreasing.
-
Local Extrema
Use the First Derivative Test to classify all local maxima and local minima.
Be sure to record both the extreme value and the point in the domain where it is attained.
-
Global Extrema
Identify the global maximum,
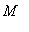 , and minimum,
, and minimum,
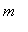 .
.
(Check that the global extrema are consistent with the range found in Step 1.)
Identify any values of
 in the domain of the function that satisfy
in the domain of the function that satisfy
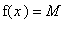 or
or
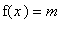 .
.
Note
: Classification of local extrema can be omitted from Step 3 if the Second Derivative Test is used in Step 4.
Step 5: Analysis Based on the Second Derivative
-
Sign Chart for
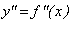
Use the possible inflection points to determine intervals of the domain where the function is concave up and where the function is concave down.
-
Local Extrema
Use the Second Derivative Test to classify all local maxima and local minima.
Be sure to record both the extreme value and the point in the domain where it is attained.
-
Inflection Points
Identify any point where the second derivative changes sign.
Note
: Classification of local extrema can be omitted from Step 4 if the First Derivative Test is used in Step 3.
Step 6: Graph the Function
-
Plot the special points identified in Steps 1-5.
-
Draw all asymptotes found in Step 3.
-
Use the sign charts to ``connect the dots''.
-
Verify that the graph is consistent with all analysis.
Example 1: Polynomial
Let
| > |
f1 := x^6-10*x^5-15*x^4+140*x^3+160*x^2-528*x-800:
F1 := unapply( f1, x ):
f(x) = f1;
|
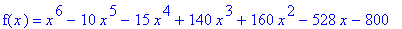
Create a graph of
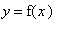 that shows all significant behavior on the entire real line.
that shows all significant behavior on the entire real line.
Steps 1-3: Analysis Based on the Function
This function is defined for all real numbers. The range is difficult to determine. Note that
| > |
q1 := Limit( f1, x=infinity ):
q1 = value( q1 );
|
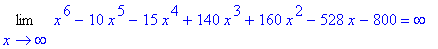
| > |
q2 := Limit( f1, x=-infinity ):
q2 = value( q2 );
|
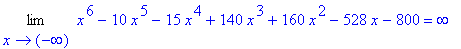
so the global maximum is +
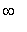 . There must be a global minimum, but we do not yet have enough information to even estimate it.
. There must be a global minimum, but we do not yet have enough information to even estimate it.
This function is neither even nor odd and is definitely not periodic. There are no endpoints to consider.
The intercept is
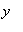 = -800, so one point on the graph is ( 0, -900 ). This information will be collected for reporting in a table immediately prior to creating the graph.
= -800, so one point on the graph is ( 0, -900 ). This information will be collected for reporting in a table immediately prior to creating the graph.
| > |
int1 := [ 0, F1(0), `intercept` ]:
int1;
|
![[0, -800, intercept]](images/Graphing34.gif)
(Note that we already have significant information suggesting that the range of this function will be very large.)
Finding roots is not possible to do by hand. As a sixth-degree polynomial, there are six zeroes but there is no general formula for these roots. Maple's
solve
command provides approximations to all six zeroes of this polynomial:
| > |
q3 := solve( f1=0., x ):
q3;
|
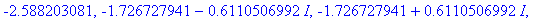
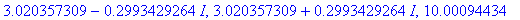
The two real-valued roots are, approximately,
| > |
q4 := op(remove( has, [q3], I )):
evalf[4]( q4 );
|
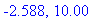
The corresponding point on the graph are ( -2.588, 0 ) and ( 10, 0 ). The information needed for the summary table is
| > |
zero1 := seq( [x,0, `zero`], x=q4 ):
evalf[4]( zero1 );
|
![[-2.588, 0., zero], [10.00, 0., zero]](images/Graphing38.gif)
Because the function is continuous and has only these two zeroes, the sign of the function can change only at these two points. The
SignChart
command (defined at the top of this worksheet) can be used to create a sign chart showing where the function is positive (pink) and negative (cyan).
| > |
SignChart( f1, x=-10..15, 0 );
|
![[Maple Plot]](images/Graphing39.gif)
Observe that we now know the global minimum must occur somewhere between -2.588 and 10.00.
There are no asymptotes.
Step 4: Analysis Based on the First Derivative
The first derivative is
| > |
df1 := diff( f1, x ):
`f '`(x) = df1;
|
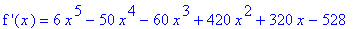
The stationary points are
| > |
stat1 := solve( df1=0., x ):
evalf[4]( stat1 );
|
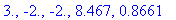
There are no endpoints and no singular points
| > |
end1 := NULL:
sing1 := NULL:
|
The critical points of this function are
| > |
crit1 := [ stat1, sing1, end1 ]:
evalf[4]( crit1 );
|
![[3., -2., -2., 8.467, .8661]](images/Graphing42.gif)
The critical points divide the domain into intervals on which the derivative does not change sign. (In the following sign chart the first derivative is positive on pink intervals and negative on cyan intervals. Note that the third argument is the order of the derivative.)
| > |
SignChart( f1, x=-10..15, 1 );
|
![[Maple Plot]](images/Graphing43.gif)
From this sign chart, and the First Derivative Test, it is clear the function has local minima where the sign chart changes from cyan to pink, i.e., at
 = 0.8661 and
= 0.8661 and
 = 8.467, and has local maxima where the sign chart changes from pink to cyan, i.e., at
= 8.467, and has local maxima where the sign chart changes from pink to cyan, i.e., at
 = 3. The corresponding points on the graph of the function are
= 3. The corresponding points on the graph of the function are
| > |
cp1 := seq( [ x, F1(x), `critical point` ], x=crit1 ):
evalf[4]( cp1 );
|
![[3., -80., `critical point`], [-2., -80., `critical point`], [-2., -80., `critical point`], [8.467, -.5262e5, `critical point`], [.8661, -1059., `critical point`]](images/Graphing47.gif)
![[3., -80., `critical point`], [-2., -80., `critical point`], [-2., -80., `critical point`], [8.467, -.5262e5, `critical point`], [.8661, -1059., `critical point`]](images/Graphing48.gif)
The global minimum can now be determined by comparison of the function values for the local minima; hence, the global minimum is -52620 and occurs near
 = 8.467.
= 8.467.
Step 5: Analysis Based on the Second Derivative
The second derivative is
| > |
ddf1 := diff( f1, x,x ):
`f ''`(x) = ddf1;
|
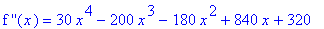
The possible inflection points are
| > |
possinfl1 := solve( ddf1=0., x ):
evalf[4]( possinfl1 );
|
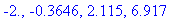
The concavity on the five intervals defined by these four points is easiest to display in terms of a sign chart for the second derivative. (Intervals where the function is concave up are shown in pink; concave down in cyan.)
| > |
SignChart( f1, x=-10..15, 2 );
|
![[Maple Plot]](images/Graphing52.gif)
There is a sign change in the second derivative at each zero of the second derivative. The coordinates of the four inflection points are
| > |
ip1 := seq( [ x, F1(x), `inflection point` ], x=[possinfl1] ):
evalf[4]( ip1 );
|
![[-2., -80., `inflection point`], [-.3646, -593.2, `inflection point`], [2.115, -510.6, `inflection point`], [6.917, -.3361e5, `inflection point`]](images/Graphing53.gif)
![[-2., -80., `inflection point`], [-.3646, -593.2, `inflection point`], [2.115, -510.6, `inflection point`], [6.917, -.3361e5, `inflection point`]](images/Graphing54.gif)
Step 6: Graph the Function
The important points identified in Steps 1-5 include the intercept, the zeroes, the critical points, and the inflection points. These can be collected in a table (sorted by increasing value of
 ):
):
| > |
important1 := sort( [ int1, zero1, cp1, ip1 ], (a,b)->a[1]<b[1] ):
tab1 := [ [`x`, `y`, `description`], [`-----`, `-----`, `---------------`], op(important1) ]:
matrix( evalf[4]( tab1 ) );
|
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [-2.588, 0., zero], [-2., -80., `inflection point`], [-2., -80., `critical point`], [-2., -80., `critical point`], [-.3646, -593.2,...](images/Graphing56.gif)
Our sketch of the function begins by plotting these points
| > |
pts1 := [seq( P[1..2], P=important1 )]:
Ppts1 := plot( pts1, color=blue, style=point, symbolsize=20 ):
display( Ppts1, view=[-10..15,DEFAULT],
title=sprintf("Important Points for\n y=%a",f1) );
|
![[Maple Plot]](images/Graphing57.gif)
The sign charts for the function and its first two derivatives are used to ``connect the dots''. (Note how a list is used in the third argument to plot multiple sign charts in one Maple plot.)
| > |
SignChart( f1, x=-10..15, [0,1,2] );
|
![[Maple Plot]](images/Graphing58.gif)
Remember that the global maximum of the function is
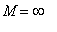 and the global minimum is
and the global minimum is
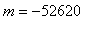 ; this means the function is going to increase very rapidly as
; this means the function is going to increase very rapidly as
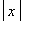 increases.
increases.
| > |
Pfn1 := plot( f1, x=-10..15, view=[DEFAULT,-53000..53000], numpoints=250 ):
display( [Ppts1, Pfn1],
title=sprintf("Important Points and Graph for\n y=%a",f1) );
|
![[Maple Plot]](images/Graphing62.gif)
On this scale it is difficult to clearly see the local extrema and inflection points. Since all but three of the ``interesting points'' are contained in the interval [-3,4], it makes sense to zoom in on that region of the function.To select a viewing window, identify the largest and smallest y-coordinate from the critical points that are to be displayed and the endpoints of the bounded interval
| > |
f(-3) = F1(-3);
f(4) = F1(4);
|
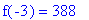
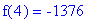
On this viewing window, the important points are
| > |
display( Ppts1, view=[-3..4,-1500..500],
title=sprintf("Important Points for\n y=%a",f1) );
|
![[Maple Plot]](images/Graphing65.gif)
and the corresponding sign chart are
| > |
SignChart( f1, x=-3..4, [0,1,2] );
|
![[Maple Plot]](images/Graphing66.gif)
With this information it is a straightforward task to complete the graph of the function. The result is
| > |
display( [Ppts1,Pfn1], view=[-3..4,-1500..500],
title=sprintf("Important Points and Graph for\n y=%a",f1) );
|
![[Maple Plot]](images/Graphing67.gif)
To conclude, it is interesting to compare our graphs with the ones produced by Maple's
FunctionChart
command. First, on the interval [-10,15]
| > |
FunctionChart( f1, -10..15, view=[DEFAULT,-53000..53000],
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/Graphing68.gif)
and also on [ -3, 4 ]
| > |
FunctionChart( f1, -3..4, view=[DEFAULT,-1500..500],
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/Graphing69.gif)
Example 2: Rational Function
Let
| > |
f2 := (-x^3+3*x^2-5*x+6)/(x^2-4*x+3):
F2 := unapply( f2, x ):
f(x) = f2;
|
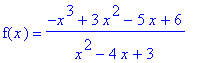
Create a graph of
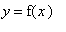 that shows all significant behavior on the entire real line.
that shows all significant behavior on the entire real line.
Steps 1-3: Analysis Based on the Function
Because the denominator of has zeroes at
| > |
q1 := solve( denom(f2)=0, x ):
q1;
|
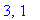
but, except for these points, the function is defined and continuous for all real numbers.
The range is (
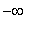 ,
,
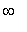 ) because
) because
| > |
q2 := Limit( f2, x=infinity ):
q2 = value( q2 );
|
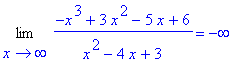
| > |
q3 := Limit( f2, x=-infinity ):
q3 = value( q3 );
|
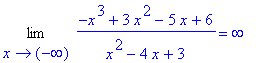
All interesting extrema will be local.
This function is neither even nor odd and is definitely not periodic. There are no endpoints to consider.
The intercept is
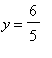 , so one point on the graph is
, so one point on the graph is
| > |
int2 := [ 0, F2(0), `intercept` ]:
int2;
|
![[0, 2, intercept]](images/Graphing78.gif)
The zeroes of the numerator of f are not obvious, but Maple reports
| > |
q4 := solve( numer(f2)=0, x );
|
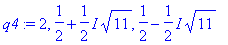
so the real-valued zero of f are
| > |
q5 := remove( has, [q4], I ):
op(q5);
|
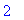
The corresponding point on the graph are
| > |
zero2 := seq( [x,0, `zero`], x=q5 ):
evalf[4]( zero2 );
|
![[2., 0., zero]](images/Graphing81.gif)
The sign chart for the function on [ -3, 4 ] is
| > |
SignChart( f2, x=-3..4, 0 );
|
![[Maple Plot]](images/Graphing82.gif)
Notice how the function changes sign at the holes in the domain and the zero of the numerator.
There are no horizontal asymptotes.
Vertical asymptotes could possibly exist at
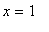 and
and
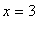 . To test both points, compute the four limits
. To test both points, compute the four limits
| > |
q6 := Limit( f2, x=1, right ):
q6 = value( q6 );
|
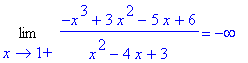
| > |
q7 := Limit( f2, x=1, left ):
q7 = value( q7 );
|
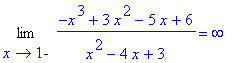
| > |
q8 := Limit( f2, x=3, right ):
q8 = value( q8 );
|
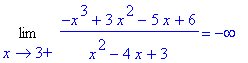
| > |
q9 := Limit( f2, x=3, left ):
q9 = value( q9 );
|
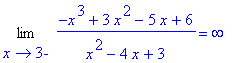
There are two vertical asymptotes:
| > |
vert2 := x=1, x=3:
vert2;
|
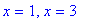
The search for an oblique asymptote is somewhat complicated. But, it is simplest to see by observing that long division yields
| > |
q10 := quo(numer(f2),denom(f2),x, 'q11'):
|
| > |
f(x) = f2;
`` = q10 + q11/denom(h2);
|
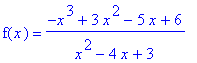
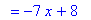
This suggests
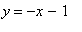 is a candidate for an asymptote of f. To confirm this
is a candidate for an asymptote of f. To confirm this
| > |
q12 := Limit( f2-q10, x=infinity ):
q12 = value( q12 );
|
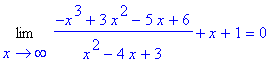
| > |
q13 := Limit( f2-q10, x=-infinity ):
q13 = value( q13 );
|
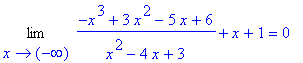
The oblique asymptote for this function is
| > |
obliq2 := y = q10:
obliq2;
|
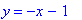
The complete set of asymptotes for this problem is
| > |
asymp2 := horiz2, vert2, obliq2:
asymp2;
|
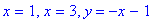
Step 4: Analysis Based on the First Derivative
The first derivative is
| > |
df2 := simplify(diff( f2, x )):
`f '`(x) = df2;
|
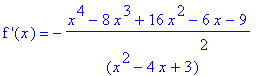
The stationary points are the real zeroes of the first derivative
| > |
q14 := solve( df2=0., x ):
stat2 := op(remove( has, [q14], I )):
evalf[4]( stat2 );
|
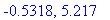
The holes in the domain are neither singular points nor endpoints.
| > |
sing2 := NULL:
end2 := NULL:
|
The critical points of this function are
| > |
crit2 := [ stat2, sing2, end2 ]:
evalf[4]( crit2 );
|
![[-.5318, 5.217]](images/Graphing99.gif)
The critical points divide the domain into intervals on which the derivative does not change sign. (In the following sign chart the first derivative is positive on pink intervals and negative on cyan intervals.)
| > |
SignChart( f2, x=-10..10, 1 );
|
![[Maple Plot]](images/Graphing100.gif)
From this sign chart, and the First Derivative Test, it is clear the function has a local minimum where the sign chart changes from cyan to pink, i.e., at
 = -0.5318, and has a local maximum where the sign chart changes from pink to cyan, i.e., at
= -0.5318, and has a local maximum where the sign chart changes from pink to cyan, i.e., at
 = 5.217. The corresponding points on the graph of the function are
= 5.217. The corresponding points on the graph of the function are
| > |
cp2 := seq( [ x, F2(x), `critical point` ], x=crit2 ):
evalf[4]( cp2 );
|
![[-.5318, 1.785, `critical point`], [5.217, -8.602, `critical point`]](images/Graphing103.gif)
The global minimum can now be determined by comparison of the function values for the local minima; hence, the global minimum is -52620 and occurs near
 = 8.467.
= 8.467.
Step 5: Analysis Based on the Second Derivative
The second derivative is
| > |
ddf2 := simplify(diff( f2, x,x )):
`f ''`(x) = ddf2;
|
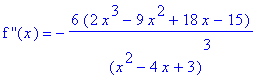
The possible inflection points are the real-valued zeroes of the second derivative:
| > |
q15 := solve( ddf2=0., x ):
possinfl2 := op(remove( has, [q15], I )):
evalf[4]( possinfl2 );
|
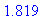
The concavity on the five intervals defined by these four points is easiest to display in terms of a sign chart for the second derivative. (Intervals where the function is concave up are shown in pink; concave down in cyan.)
| > |
SignChart( f2, x=-10..10, 2 );
|
![[Maple Plot]](images/Graphing107.gif)
There is a sign change in the second derivative at the zero -- and at each hole in the domain. The coordinates on the inflection point in the domain is
| > |
ip2 := seq( [ x, F2(x), `inflection point` ], x=[possinfl2] ):
evalf[4]( ip2 );
|
![[1.819, -.8405, `inflection point`]](images/Graphing108.gif)
Step 6: Graph the Function
The important points identified in Steps 1-5 include the intercept, the zeroes, the critical points, and the inflection point. These can be collected in a table (sorted by increasing value of
 ):
):
| > |
important2 := sort( [ int2, zero2, cp2, ip2 ], (a,b)->a[1]<b[1] ):
tab2 := [ [`x`, `y`, `description`], [`-----`, `-----`,`---------------`], op(important2) ]:
matrix( evalf[4]( tab2 ) );
|
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [-.5318, 1.785, `critical point`], [0., 2., intercept], [1.819, -.8405, `inflection point`], [2., 0., zero], [5.217, -8.602, `criti...](images/Graphing110.gif)
Our sketch of the function begins by plotting these points
| > |
pts2 := [seq( P[1..2], P=important2 )]:
Ppts2 := plot( pts2, color=blue, style=point, symbolsize=20 ):
display( Ppts2, view=[-10..10,DEFAULT],
title=sprintf("Important Points for\n y=%a",f2) );
|
![[Maple Plot]](images/Graphing111.gif)
| > |
SignChart( f2, x=-10..10, [0,1,2] );
|
![[Maple Plot]](images/Graphing112.gif)
Looking at these points and the classification of each point it might appear to be impossible to ``connect the dots'' following what we know about the sign of the function and its first two derivatives. But, remember that there are two points where the function is discontinuous. When the asymptotes are added, the picture becomes a little clearer.
| > |
Pasym2 := implicitplot( {asymp2}, x=-10..15, y=-20..10, color=sienna ):
display( [Ppts2,Pasym2],
title=sprintf("Important Points and Asymptotes for\n f(x)=%a", f2) );
|
![[Maple Plot]](images/Graphing113.gif)
The behavior of the function at each asymptote, combined with the local extrema and inflection point results, provides enough information to complete the graph.
| > |
Pfn2 := plot( f2, x=-10..15, discont=true,
view=[DEFAULT,-20..10], numpoints=250 ):
display( [Ppts2, Pasym2, Pfn2],
title=sprintf("Important Points, Asymptotes, and Graph for\n y=%a",f1) );
|
![[Maple Plot]](images/Graphing114.gif)
To conclude, it is interesting to compare our graphs with the ones produced by Maple's
FunctionChart
command. First, on the interval [-10,15]
| > |
FunctionChart( f2, -10..15, view=[DEFAULT,-20..10],
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/Graphing115.gif)
Example 3: Plotting a Parametric Family of Functions
Let
| > |
f3 := 10/(x^2+6*x+c):
F3 := unapply( f3, x ):
f(x) = f3;
|
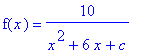
Determine the value of
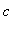 for where the graphs of
for where the graphs of
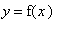 undergo a significant change in appearance. Prepare one plot containing representative graphs of each type.
undergo a significant change in appearance. Prepare one plot containing representative graphs of each type.
The key to this problem is the denominator. Completing the square on this quadratic allows the denominator to be rewritten as
| > |
q1 := denom( f3 ):
q1 = student[completesquare]( q1, x );
|
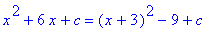
There are three cases to consider:
-
If
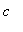 > 9 then the denominator is strictly positive for all
> 9 then the denominator is strictly positive for all
 , i.e., the domain is (
, i.e., the domain is (
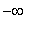 ,
,
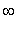 ).
).
-
If
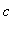 = 9 then the denominator is zero for
= 9 then the denominator is zero for
 = -3, i.e., the domain is the union of (
= -3, i.e., the domain is the union of (
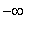 , -3 ) and ( 3,
, -3 ) and ( 3,
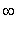 ).
).
-
If
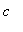 < 9 then the denominator is zero for
< 9 then the denominator is zero for
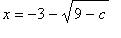 and
and
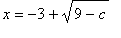 , i.e., the domain is the union of three disjoint sets.
, i.e., the domain is the union of three disjoint sets.
Based on this analysis it appears the critical value of the parameter is
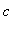 = 9.
= 9.
Steps 1-3: Analysis Based on the Function
The different domains for the three cases have already been noted:
-
for
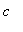 > 9:
> 9:
| > |
domain3a := [-infinity,infinity]:
domain3a;
|
![[-infinity, infinity]](images/Graphing133.gif)
-
for
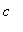 = 9:
= 9:
| > |
domain3b := [ x<>-3 ]:
domain3b;
|
![[x <> -3]](images/Graphing135.gif)
-
for
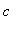 < 9:
< 9:
| > |
domain3c := [ x<>-3+sqrt(9-c), x<>-3-sqrt(9-c) ]:
domain3c;
|
![[x <> -3+(9-c)^(1/2), x <> -3-(9-c)^(1/2)]](images/Graphing137.gif)
A table comparing properties of this function for the three different cases will be created. The following will be used to make one line of this table.
| > |
domain3 := [ `domain`, domain3a, domain3b, domain3c ]:
|
To check for horizontal asymptotes, consider
| > |
q1 := Limit( f3, x=infinity ):
q1 = value( q1 );
|
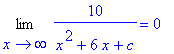
| > |
q2 := Limit( f3, x=-infinity ):
q2 = value( q2 );
|
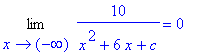
Thus, all three cases have the horizontal asymptote
| > |
horiz3a := y = 0:
horiz3b := horiz3a:
horiz3c := horiz3a:
|
| > |
horiz3 := [ `horiz. asymp.`, horiz3a, horiz3b, horiz3c ]:
|
The search for vertical asymptotes produces different results for different values of
 :
:
-
for
 > 9, there are no vertical asymptotes
> 9, there are no vertical asymptotes
-
for
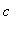 = 9, there is one vertical asymptote at
= 9, there is one vertical asymptote at
| > |
vert3b := x = -3:
vert3b;
|
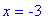
-
for
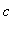 < 9, there are two vertical asymptotes at x
< 9, there are two vertical asymptotes at x
| > |
vert3c := [ x = -3-sqrt(9-c), x=-3+sqrt(9-c) ]:
vert3c;
|
![[x = -3-(9-c)^(1/2), x = -3+(9-c)^(1/2)]](images/Graphing145.gif)
| > |
vert3 := [ `vert. asymp.`, vert3a, vert3b, vert3c ]:
|
For no value of
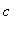 is the function even or odd or periodic.
is the function even or odd or periodic.
When
 = 0 is in the domain (and
= 0 is in the domain (and
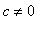 ), the intercept is
), the intercept is
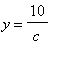 .
.
| > |
int3a := [ 0, 10/c ]:
int3b := int3a:
int3c := int3a:
int3 := [`intercept`, int3a, int3b, int3c ]:
|
Step 4: Analysis Based on the First Derivative
The first derivative,
| > |
df3 := simplify(diff( f3, x )):
`f '`(x) = df3;
|
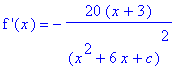
is defined on the same domain as the original function (regardless of the value of
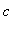 ). As a result there are no singular points and no endpoints.
). As a result there are no singular points and no endpoints.
| > |
sing3 := NULL:
end3 := NULL:
|
The zero of the numerator of the first derivative is
| > |
stat3 := solve( numer(df3)=0, x ):
evalf[4]( stat3 );
|
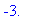
Note that
-
when
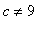 there is a single critical point
there is a single critical point
| > |
crit3a := [seq( x=z, z=[ stat3, sing3, end3 ] )]:
crit3c := crit3a:
crit3a;
|
![[x = -3]](images/Graphing154.gif)
-
for
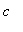 = 9,
= 9,
 = -3 is not in the domain of the function and so there are no critical points.
= -3 is not in the domain of the function and so there are no critical points.
| > |
crit3b := `none`:
crit3c := `none`:
|
| > |
crit3 := [ `critical point`, crit3a, crit3b, crit3c ]:
|
A closer look at the first derivative indicates that
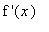 > 0 for all
> 0 for all
 < -3 (and in the domain of f) and
< -3 (and in the domain of f) and
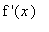 < 0 for all
< 0 for all
 > -3 (and in the domain of f). In particular, for
> -3 (and in the domain of f). In particular, for
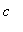 > 9, the function is increasing to the left of
> 9, the function is increasing to the left of
 = -3, decreasing to the right of
= -3, decreasing to the right of
 = -3, and
= -3, and
 = -3 is a local maximum.
= -3 is a local maximum.
| > |
lextrema3 := [ `local extrema`, `maximum`, `none`, `maximum` ]:
|
Step 5: Analysis Based on the Second Derivative
The second derivative is
| > |
ddf3 := simplify(diff( f3, x,x )):
`f ''`(x) = ddf3;
|
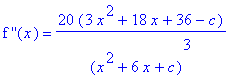
The possible inflection points are the real-valued zeroes of the second derivative:
| > |
q3 := solve( ddf3=0, x ):
q4 := [seq( x=z, z=[q3] )]:
q4;
|
![[x = -3+1/3*(-27+3*c)^(1/2), x = -3-1/3*(-27+3*c)^(1/2)]](images/Graphing166.gif)
Once again, this depends on the parameter:
-
if
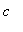 > 9, both zeroes are real and in the domain of f is
> 9, both zeroes are real and in the domain of f is
| > |
possinfl3a := q4:
possinfl3a;
|
![[x = -3+1/3*(-27+3*c)^(1/2), x = -3-1/3*(-27+3*c)^(1/2)]](images/Graphing168.gif)
-
if
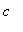 = 9, there is only one potential possible inflection point, but recall that
= 9, there is only one potential possible inflection point, but recall that
 = -3 is not in the domain for this value of
= -3 is not in the domain for this value of
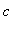
| > |
possinfl3b := vert3b:
possinfl3b;
|
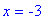
-
if
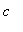 < 9, there are no real-valued solutions to
< 9, there are no real-valued solutions to
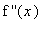 = 0 but the concavity could change at the two vertical asymptotes
= 0 but the concavity could change at the two vertical asymptotes
| > |
possinfl3c := vert3c:
possinfl3c;
|
![[x = -3-(9-c)^(1/2), x = -3+(9-c)^(1/2)]](images/Graphing175.gif)
When f '' is evaluated on each subinterval identified above, it is found that
-
for
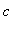 > 9 the function is concave up except between the two inflection points where the function is concave down
> 9 the function is concave up except between the two inflection points where the function is concave down
| > |
inflpt3a := possinfl3a:
|
-
for
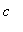 = 9 the function is concave up to the left and right of
= 9 the function is concave up to the left and right of
 = -3
= -3
-
for
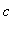 < 9 the function is concave up on the two unbounded intervals and is concave down on the interval between the two singularities
< 9 the function is concave up on the two unbounded intervals and is concave down on the interval between the two singularities
| > |
inflpt3c := possinfl3c:
|
| > |
inflpt3 := [`infl. pt.`, inflpt3a, inflpt3b, inflpt3c ]:
|
Step 6: Graph the Function
Steps 1-5 have revealed a number of differences between the graphs for
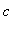 > 9,
> 9,
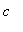 = 9, and
= 9, and
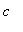 < 9. The similarities and differences are summarized in the following table.
< 9. The similarities and differences are summarized in the following table.
| > |
matrix( [ [`category`, `c > 9`, `c = 9`, `c < 9`],
[`-------------------`, `----------------------`, `----------------------`, `----------------------`],
domain3, horiz3, vert3, int3, crit3, lextrema3, inflpt3 ] );
|
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing183.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing184.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing185.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing186.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing187.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing188.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing189.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing190.gif)
![matrix([[category, `c > 9`, `c = 9`, `c < 9`], [`-------------------`, `----------------------`, `----------------------`, `----------------------`], [domain, [-infinity, infinity], [x <> -3], [x <> -3...](images/Graphing191.gif)
An animation containing plots for different values of
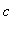 shows the results very nicely.
shows the results very nicely.
| > |
Clist := [2*($0..4),8.5,9,9.5,2*($5..9)]:
|
| > |
COLORS := red,blue,green,sienna,pink,cyan:
COLORS := [COLORS,COLORS,COLORS]:
|
| > |
p1 := seq( plot( eval(f3,c=Clist[i]),
x=-10..6,
discont=true,
color=COLORS[i],
title=sprintf("Plot of 1/(x^2+6*x+c)\n for c=%a",Clist[i]) ),
i=1..nops(Clist) ):
|
| > |
display( [p1], view=[DEFAULT,-40..30], insequence=true );
|
![[Maple Plot]](images/Graphing193.gif)
Or, with all plots in a single frame:
| > |
display( [p1], view=[DEFAULT,-40..30],
title=sprintf("Plots of 1/(x^2+6*x+c)\n for c=%a",Clist) );
|
![[Maple Plot]](images/Graphing194.gif)
And, finally, an animation of the
FunctionChart
plots are very informative.
| > |
p2 := [seq(
FunctionChart( factor(f3), -10..6, view=[DEFAULT,-40..30],
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] ),
c=Clist )]:
|
| > |
display( p2, insequence=true );
|
![[Maple Plot]](images/Graphing195.gif)
Example 4: Periodic Function
Let
| > |
f4 := sin(4*x+1/2)*cos(x/2):
F4 := unapply( f4, x ):
f(x) = f4;
|
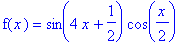
Create a graph of
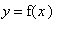 that shows all significant behavior of the function..
that shows all significant behavior of the function..
Steps 1-3: Analysis Based on the Function
This function is defined for all real numbers. Because each term in the product has range [ -1, 1 ], their product will take on values on [ -1, 1 ]. Whether the range is [ -1, 1 ] or a subset of [ -1, 1 ] is not important at this time.
This function is neither even nor odd,
| > |
simplify( F4(-x)-F4(x) );
|
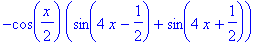
| > |
simplify( F4(-x)+F4(x) );
|
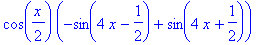
but is periodic with period
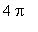 .
.
| > |
simplify( F4(x+4*Pi)-F4(x) );
|
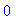
Because the function is periodic it suffices to sketch its graph on one period. If we choose to work on the interval [ 0,
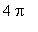 ], then the endpoints are
], then the endpoints are
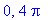
The intercept is
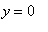 , so one point on the graph is
, so one point on the graph is
| > |
int4 := [ 0, F4(0), `intercept` ]:
int4;
|
![[0, sin(1/2), intercept]](images/Graphing205.gif)
The function will be zero whenever either factor is zero. The solutions to
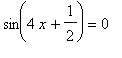 satisfy
satisfy
| > |
q1 := 4*x+1/2 = i*Pi:
q1;
|
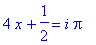
That is,
| > |
q2 := isolate( q1, x ):
q2;
|
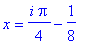
for an integer
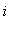 . The zeroes in [ 0,
. The zeroes in [ 0,
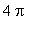 ] are
] are
| > |
q3 := seq( rhs(q2), i=1..16 ):
q3;
|
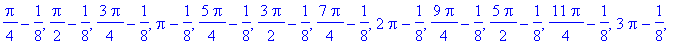
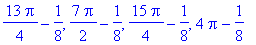
Likewise the zeroes of
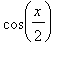 are
are
| > |
q4 := x/2 = Pi/2 + i*Pi:
q4;
|
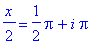
where
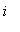 is an integer. The zeroes in [ 0,
is an integer. The zeroes in [ 0,
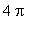 ] are
] are
| > |
q5 := seq( solve(q4,x), i=0..1 ):
q5;
|
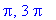
The first points on the graph are the 18 zeroes of the product on [ 0,
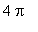 ]:
]:
| > |
zero4 := seq( [x,0, `zero`], x=[q3,q5] ):
evalf[4]( zero4 );
|
![[.6605, 0., zero], [1.446, 0., zero], [2.231, 0., zero], [3.017, 0., zero], [3.803, 0., zero], [4.588, 0., zero], [5.373, 0., zero], [6.159, 0., zero], [6.945, 0., zero], [7.730, 0., zero], [8.515, 0.,...](images/Graphing219.gif)
![[.6605, 0., zero], [1.446, 0., zero], [2.231, 0., zero], [3.017, 0., zero], [3.803, 0., zero], [4.588, 0., zero], [5.373, 0., zero], [6.159, 0., zero], [6.945, 0., zero], [7.730, 0., zero], [8.515, 0.,...](images/Graphing220.gif)
![[.6605, 0., zero], [1.446, 0., zero], [2.231, 0., zero], [3.017, 0., zero], [3.803, 0., zero], [4.588, 0., zero], [5.373, 0., zero], [6.159, 0., zero], [6.945, 0., zero], [7.730, 0., zero], [8.515, 0.,...](images/Graphing221.gif)
![[.6605, 0., zero], [1.446, 0., zero], [2.231, 0., zero], [3.017, 0., zero], [3.803, 0., zero], [4.588, 0., zero], [5.373, 0., zero], [6.159, 0., zero], [6.945, 0., zero], [7.730, 0., zero], [8.515, 0.,...](images/Graphing222.gif)
The sign chart for the function on [ 0,
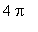 ] is
] is
| > |
SignChart( f4, x=0..4*Pi, 0 );
|
![[Maple Plot]](images/Graphing224.gif)
Notice that some of the adjacent zeroes are so close that they are not visible on this sign chart.
The continuity of the function on [ 0,
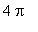 ] means there can be no vertical asymptotes. Likewise, because the domain is bounded there are no horizontal or oblique asymptotes.
] means there can be no vertical asymptotes. Likewise, because the domain is bounded there are no horizontal or oblique asymptotes.
Step 4: Analysis Based on the First Derivative
The first derivative is
| > |
df4 := simplify(diff( f4, x )):
`f '`(x) = df4;
|
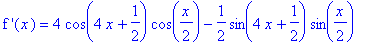
The stationary points are the real zeroes of the first derivative
| > |
q6 := solve( df4=0., x ):
evalf[4]( q6 );
|
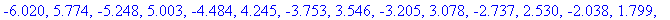
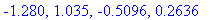
Note that these zeroes are in the interval [
 ,
,
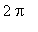 ]. By periodicity, the zeroes in [
]. By periodicity, the zeroes in [
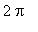 ,
,
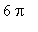 ] can be obtained by adding
] can be obtained by adding
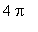 to each of the above zeroes.
to each of the above zeroes.
| > |
q7 := seq(evalf(z+4*Pi),z=[q6]):
stat4 := op(select( InInterval, [q6,q7], [0,evalf(4*Pi)] )):
evalf[4]( stat4 );
|
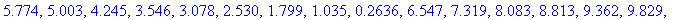
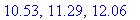
There are no singular points and we have already identified the endpoints.
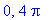
The critical points of this function are
| > |
crit4 := [ stat4, sing4, end4 ]:
evalf[4]( crit4 );
|
![[5.774, 5.003, 4.245, 3.546, 3.078, 2.530, 1.799, 1.035, .2636, 6.547, 7.319, 8.083, 8.813, 9.362, 9.829, 10.53, 11.29, 12.06, 0., 12.57]](images/Graphing237.gif)
![[5.774, 5.003, 4.245, 3.546, 3.078, 2.530, 1.799, 1.035, .2636, 6.547, 7.319, 8.083, 8.813, 9.362, 9.829, 10.53, 11.29, 12.06, 0., 12.57]](images/Graphing238.gif)
The critical points divide the domain into intervals on which the derivative does not change sign. (In the following sign chart the first derivative is positive on pink intervals and negative on cyan intervals.)
| > |
SignChart( f4, x=0..4*Pi, 1 );
|
![[Maple Plot]](images/Graphing239.gif)
From this sign chart, and the First Derivative Test, it is clear the function has a local minimum at each of the nine points where the sign chart changes from cyan to pink and has a local maximum at the nine points where the sign chart changes from pink to cyan. (Only the two endpoints are not local extrema.) The corresponding points on the graph of the function are
| > |
cp4 := seq( [ x, F4(x), `critical point` ], x=crit4 ):
evalf[4]( cp4 );
|
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing240.gif)
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing241.gif)
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing242.gif)
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing243.gif)
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing244.gif)
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing245.gif)
![[5.774, .9672, `critical point`], [5.003, -.7987, `critical point`], [4.245, .5136, `critical point`], [3.546, -.1715, `critical point`], [3.078, .7731e-2, `critical point`], [2.530, -.2801, `critical ...](images/Graphing246.gif)
These points show that the range is [ -0.9912, 0.9912 ]
Step 5: Analysis Based on the Second Derivative
The second derivative is
| > |
ddf4 := simplify(diff( f4, x,x )):
`f ''`(x) = ddf4;
|
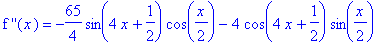
The possible inflection points are the real-valued zeroes of the second derivative:
| > |
q8 := solve( ddf4=0., x ):
evalf[4]( q8 );
|
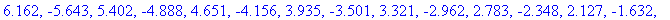
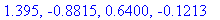
Shifting these solutions by
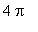 then removing those outside [ 0,
then removing those outside [ 0,
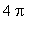 ] yields a list of 18 possible inflection points.
] yields a list of 18 possible inflection points.
| > |
q9 := seq(evalf(z+4*Pi),z=[q8]):
possinfl4 := op(select( InInterval, [q8,q9], [0,evalf(4*Pi)] )):
evalf[4]( possinfl4 );
|
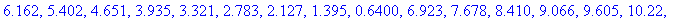
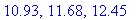
The concavity on the intervals defined by these 18 points is easiest to display in terms of a sign chart for the second derivative. (Intervals where the function is concave up are shown in pink; concave down in cyan.)
| > |
SignChart( f4, x=0..4*Pi, 2 );
|
![[Maple Plot]](images/Graphing254.gif)
There is a sign change in the second derivative at point where
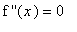 . The coordinates on the inflection point in the domain is
. The coordinates on the inflection point in the domain is
| > |
ip4 := seq( [ x, F4(x), `inflection point` ], x=[possinfl4] ):
evalf[4]( ip4 );
|
![[6.162, -.1491e-1, `inflection point`], [5.402, .1043, `inflection point`], [4.651, -.1734, `inflection point`], [3.935, .1957, `inflection point`], [3.321, -.8434e-1, `inflection point`], [2.783, -.14...](images/Graphing256.gif)
![[6.162, -.1491e-1, `inflection point`], [5.402, .1043, `inflection point`], [4.651, -.1734, `inflection point`], [3.935, .1957, `inflection point`], [3.321, -.8434e-1, `inflection point`], [2.783, -.14...](images/Graphing257.gif)
![[6.162, -.1491e-1, `inflection point`], [5.402, .1043, `inflection point`], [4.651, -.1734, `inflection point`], [3.935, .1957, `inflection point`], [3.321, -.8434e-1, `inflection point`], [2.783, -.14...](images/Graphing258.gif)
![[6.162, -.1491e-1, `inflection point`], [5.402, .1043, `inflection point`], [4.651, -.1734, `inflection point`], [3.935, .1957, `inflection point`], [3.321, -.8434e-1, `inflection point`], [2.783, -.14...](images/Graphing259.gif)
![[6.162, -.1491e-1, `inflection point`], [5.402, .1043, `inflection point`], [4.651, -.1734, `inflection point`], [3.935, .1957, `inflection point`], [3.321, -.8434e-1, `inflection point`], [2.783, -.14...](images/Graphing260.gif)
![[6.162, -.1491e-1, `inflection point`], [5.402, .1043, `inflection point`], [4.651, -.1734, `inflection point`], [3.935, .1957, `inflection point`], [3.321, -.8434e-1, `inflection point`], [2.783, -.14...](images/Graphing261.gif)
Step 6: Graph the Function
The important points identified in Steps 1-5 include the intercept, the zeroes, the critical points, and the inflection points. These can be collected in a table (sorted by increasing value of
 ):
):
| > |
important4 := sort( evalf([ int4, zero4, cp4, ip4 ]), (a,b)->a[1]<b[1] ):
tab4 := [ [`x`, `y`, `description`], [`-----`, `-----`,`---------------`], op(important4) ]:
matrix( evalf[4]( tab4 ) );
|
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [0., .4794, `critical point`], [0., .4794, intercept], [.2636, .9912, `critical point`], [.6400, .7718e-1, `inflection point`], [.6...](images/Graphing263.gif)
This is a long list. But, each point in this table is important. When these points are plotted
| > |
pts4 := [seq( P[1..2], P=important4 )]:
Ppts4 := plot( pts4, color=blue, style=point, symbolsize=20 ):
display( Ppts4,
title=sprintf("Important Points for\n y=%a",f4) );
|
![[Maple Plot]](images/Graphing264.gif)
| > |
SignChart( f4, x=0..4*Pi, [0,1,2] );
|
![[Maple Plot]](images/Graphing265.gif)
It is now a fairly simple matter to obtain an accurate graph by connecting these points in succession.
| > |
Pfn4 := plot( f4, x=0..4*Pi ):
display( [Ppts4, Pfn4],
title=sprintf("Important Points, Asymptotes, and Graph for\n y=%a",f4) );
|
![[Maple Plot]](images/Graphing266.gif)
To conclude, it is interesting to compare our graphs with the ones produced by Maple's
FunctionChart
command on the interval [ 0, 4*Pi ]
| > |
FunctionChart( f4, 0..4*Pi,
pointoptions=[symbolsize=20],
slope=[thickness(2,2), color(red,blue)],
concavity=[filled(pink,cyan)] );
|
![[Maple Plot]](images/Graphing267.gif)
Example 5: Reconstructing a Function from Its First Derivative
Let f be an unspecified function with the properties that
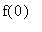 = -10, and
= -10, and
| > |
df5 := (x-4)*(x-2)/sqrt(x):
dF5 := unapply( f5, x ):
`f '`(x) = df5;
|
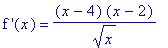
Determine all information needed to create a graph of the function f. In particular, create the table of important points and the sign charts for the first and second derivative. Then, draw the function by hand.
Steps 1-3: Analysis Based on the Function
Because we do not have an explicit formula for the function, there is not much to do in Steps 1-3.
Step 4: Analysis Based on the First Derivative
The first derivative is
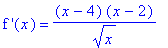
The stationary points are the real zeroes of the first derivative
| > |
stat5 := solve( df5=0., x ):
evalf[4]( stat5 );
|
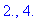
The fact that the derivative exists only for
 > 0 means the function f must be continuous for all
> 0 means the function f must be continuous for all
 > 0 (and, possibly,
> 0 (and, possibly,
 = 0).
= 0).
| > |
sing5 := NULL:
end5 := 0:
|
The critical points of this function are
| > |
crit5 := [ stat5, sing5, end5 ]:
evalf[4]( crit5 );
|
![[2., 4., 0.]](images/Graphing275.gif)
The critical points divide the domain into intervals on which the derivative does not change sign. (In the following sign chart the first derivative is positive on pink intervals and negative on cyan intervals.)
| > |
SignChart( df5, x=0..10, 0 );
|
![[Maple Plot]](images/Graphing276.gif)
From this sign chart, and the First Derivative Test, it is clear the function has a local minimum at
 = 4 and has a local maximum at
= 4 and has a local maximum at
 = 2. Also, because the derivative is positive immediately to the right of
= 2. Also, because the derivative is positive immediately to the right of
 = 0, this endpoint is a local minimum. (There is nothing that can be said about global extrema.) All that is known about function values at the critical points is summarized below:
= 0, this endpoint is a local minimum. (There is nothing that can be said about global extrema.) All that is known about function values at the critical points is summarized below:
| > |
cp5 := [ 0, -10, `endpoint` ],
[ 0, -10, `local minimum` ],
[ 2, `>-10`, `local maximum` ],
[ 4, `<f(2)`, `local minimum` ]:
cp5;
|
![[0, -10, endpoint], [0, -10, `local minimum`], [2, `>-10`, `local maximum`], [4, `<f(2)`, `local minimum`]](images/Graphing280.gif)
Step 5: Analysis Based on the Second Derivative
The second derivative is
| > |
ddf5 := simplify(diff( df5, x )):
`f ''`(x) = ddf5;
|
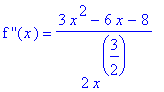
The possible inflection points are the real-valued zeroes of the second derivative:
| > |
q1 := solve( ddf5=0., x ):
evalf[4]( q1 );
|
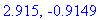
The only possible inflection point is the root in the domain of the function:
| > |
possinfl5 := op(select( InInterval, [q1], [0,10] )):
evalf[4]( possinfl5 );
|
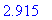
The concavity on the two intervals defined by this one point is easiest to display in terms of a sign chart for the second derivative.
| > |
SignChart( df5, x=0..10, 1 );
|
![[Maple Plot]](images/Graphing284.gif)
There is one inflection point. a sign change in the second derivative at the zero. The coordinates on the inflection point in the domain is not known, but because the function is decreasing on ( 2, 4 ) we know f(2) > f(2.915) > f(4):
| > |
ip5 := seq( [ x, `<f(2) & >f(4)`, `inflection point` ], x=[possinfl5] ):
evalf[4]( ip5 );
|
![[2.915, `<f(2) & >f(4)`, `inflection point`]](images/Graphing285.gif)
Step 6: Graph the Function
The important points identified in Steps 4 & 5 include the intercept, the zeroes, the critical points, and the inflection point. These can be collected in a table (sorted by increasing value of
 ):
):
| > |
important5 := sort( [ cp5, ip5 ], (a,b)->a[1]<b[1] ):
tab5 := [ [`x`, `y`, `description`], [`-----`, `-----`,`---------------`], op(important5) ]:
matrix( evalf[4]( tab5 ) );
|
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [0., -10., `local minimum`], [0., -10., endpoint], [2., `>-10`, `local maximum`], [2.915, `<f(2) & >f(4)`, `inflection point`], [4....](images/Graphing287.gif)
This is the table of important values that is requested at the outset of the problem. It is not difficult to sketch the general shape of the function from this information and the sign charts for the first and second derivatives
| > |
SignChart( df5, x=0..10, [0,1] );
|
![[Maple Plot]](images/Graphing288.gif)
Lesson Summary
The task of creating the graph of a function can be subdivided into the analysis of the function, the first derivative, and the second derivative. Some of the conclusions, e.g., the classification of local extrema, can be done in more than one stage of the process. From a table of important values compiled during the analysis and the sign charts for the function and its first two derivatives, it is usually fairly easy to complete the sketch by ``connecting the dots''.
You are encouraged to use Maple at any time while solving these problems. Remember, however, to avoid using Maple to plot the function until you have discovered all of the properties of the graph. Use the
FunctionChart
, in the
Student[Calculus1]
package, command only as a check of your work.
As for the use of maplets, the
FunctionAnalyzer
maplet [
Maplet Viewer][
MapleNet] is recommended over the
CurveAnalysis
[
Maplet Viewer][
MapleNet] and
DerivativePlot
[
Maplet Viewer][
MapleNet] maplets.
![]()
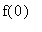 ).
).
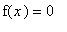 .
. , 0 ) where
, 0 ) where
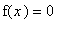 .
.
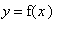
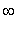 or
or
 , compute the corresponding limit at infinity.
, compute the corresponding limit at infinity.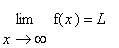 , then
, then
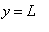 is a horizontal asymptote.
is a horizontal asymptote.
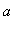 , if either one-sided limit of f at
, if either one-sided limit of f at
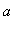 is infinite, then
is infinite, then
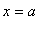 is a vertical asymptote.
is a vertical asymptote.
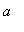 and
and
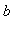 such that either
such that either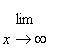
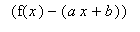 = 0 or
= 0 or
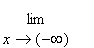
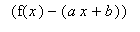 = 0,
= 0, 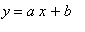 is an oblique asymptote.
is an oblique asymptote.
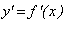
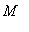 , and minimum,
, and minimum,
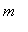 .
. in the domain of the function that satisfy
in the domain of the function that satisfy
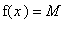 or
or
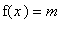 .
.
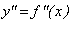
![[Maple Plot]](images/Graphing39.gif)
![[Maple Plot]](images/Graphing43.gif)
![[Maple Plot]](images/Graphing52.gif)
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [-2.588, 0., zero], [-2., -80., `inflection point`], [-2., -80., `critical point`], [-2., -80., `critical point`], [-.3646, -593.2,...](images/Graphing56.gif)
![[Maple Plot]](images/Graphing57.gif)
![[Maple Plot]](images/Graphing58.gif)
![[Maple Plot]](images/Graphing62.gif)
![[Maple Plot]](images/Graphing65.gif)
![[Maple Plot]](images/Graphing66.gif)
![[Maple Plot]](images/Graphing67.gif)
![[Maple Plot]](images/Graphing68.gif)
![[Maple Plot]](images/Graphing69.gif)
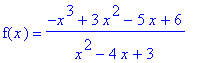
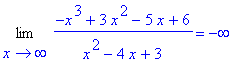
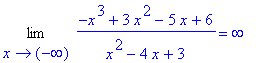
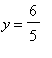 , so one point on the graph is
, so one point on the graph is
![[Maple Plot]](images/Graphing82.gif)
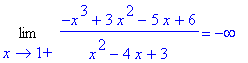
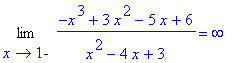
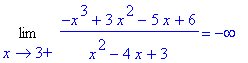
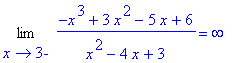
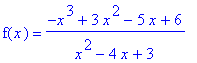
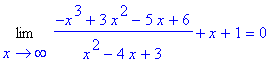
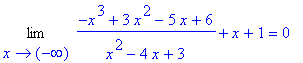
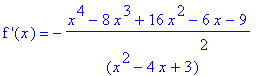
![[Maple Plot]](images/Graphing100.gif)
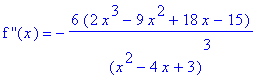
![[Maple Plot]](images/Graphing107.gif)
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [-.5318, 1.785, `critical point`], [0., 2., intercept], [1.819, -.8405, `inflection point`], [2., 0., zero], [5.217, -8.602, `criti...](images/Graphing110.gif)
![[Maple Plot]](images/Graphing111.gif)
![[Maple Plot]](images/Graphing112.gif)
![[Maple Plot]](images/Graphing113.gif)
![[Maple Plot]](images/Graphing114.gif)
![[Maple Plot]](images/Graphing115.gif)
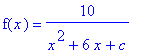
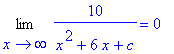
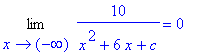
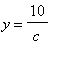 .
.
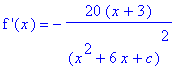
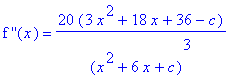
![[Maple Plot]](images/Graphing193.gif)
![[Maple Plot]](images/Graphing194.gif)
![[Maple Plot]](images/Graphing195.gif)
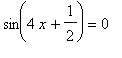 satisfy
satisfy
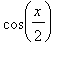 are
are
![[Maple Plot]](images/Graphing224.gif)
![[Maple Plot]](images/Graphing239.gif)
![[Maple Plot]](images/Graphing254.gif)
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [0., .4794, `critical point`], [0., .4794, intercept], [.2636, .9912, `critical point`], [.6400, .7718e-1, `inflection point`], [.6...](images/Graphing263.gif)
![[Maple Plot]](images/Graphing264.gif)
![[Maple Plot]](images/Graphing265.gif)
![[Maple Plot]](images/Graphing266.gif)
![[Maple Plot]](images/Graphing267.gif)
![[Maple Plot]](images/Graphing276.gif)
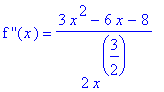
![[Maple Plot]](images/Graphing284.gif)
![matrix([[x, y, `description`], [`-----`, `-----`, `---------------`], [0., -10., `local minimum`], [0., -10., endpoint], [2., `>-10`, `local maximum`], [2.915, `<f(2) & >f(4)`, `inflection point`], [4....](images/Graphing287.gif)
![[Maple Plot]](images/Graphing288.gif)