RiemannSum.mws
Riemann Sums
| > |
restart;
with( plots ):
with( plottools ):
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
Auxiliary Procedures (do not modify)
| > |
SpherePyramid := proc( N::posint )
local COLORS, layer;
layer := proc( n, N, C )
local CTR, G;
G := seq( -(n-1)+2*i, i=0..n-1 );
CTR := [seq( seq( [i,j,N+1-n], j=G ), i=G )];
return seq( sphere( c, 1, color=C ), c=CTR );
end proc:
COLORS := [ red, blue, green, cyan, pink,
magenta, navy, orange, violet, wheat ]:
display( seq( layer( i, N, COLORS[i] ), i=1..N ),
view=[-(N+2)..N+2,-(N+2)..N+2,-2..N+2],
style=patchnogrid, axes=boxed );
end proc:
|
| > |
RiemannSumComparison := proc( F, A, B, Part, Meth )
local MM;
MM := Matrix( nops(Part), nops(Meth), (i,j)->evalf(ApproximateInt( F, x=A..B, partition=Part[i], method=Meth[j] )) ):
< < `` | op(Meth) >,
< Vector(Part) | MM > >;
end proc:
|
| > |
S3 := SpherePyramid( 3 ):
|
Lesson Overview
This lesson lays the foundation for the definition of the
Definite Integral. The specific objectives of this lesson are
-
introduce sigma notation and learn some basic summation formulae,
-
use rectangles to approximate the area under the graph of a positive function,
-
define a Riemann sum of a function on a partition, and
-
associate Riemann sums and areas approximated by rectangles.
These topics are not directly related to the discussions of
Indefinite Integrals or
Differential Equations found earlier in this unit. There is a connection between the earlier lessons and this material, but that will not be seen until the
Fundamental Theorems of Calculus lesson later in this unit.
The development of a visual understanding of Riemann Sums is aided by the use of the ApproximateInt command from the Student[Calculus1] package and the
ApproximateIntegration
maplet [
Maplet Viewer][
MapleNet].
Maplet Comment:
RiemannSum
The
RiemannSum
maplet is much too simple to be of much use. It uses only the midpoint and does not show a value for the Riemann Sum. I suppose the main use would be to help students develop the ability to recognize a sum as a Riemann sum.
Sigma Notation for Sums
Consider the pyramid built in 3 layers. Each layer is constructed from identical spheres. The bottoom layer is a 3x3 array of spheres, the middle layer is a 2x2 array of spheres, an the top layer consists of a single sphere. Clearly, this pyramid contains a total of
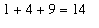 spheres.
spheres.
![[Maple Plot]](images/RiemannSum2.gif)
How many spheres are in a pyramid built with 10 layers?
| > |
#S10; # this command takes minutes to complete
|
Link to Graphical Output
The graphical output from the previous command is saved in a
separate worksheet.
The number of spheres in this plot is fairly obvious 1 + 4 + 9 + 16 + ... + 81 + 100 or, using
sigma notation
,
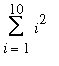 . This expression is read as ``the sum of
. This expression is read as ``the sum of
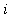 squared from
squared from
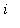 equals 1 to 10''. The capital Greek letter sigma,
equals 1 to 10''. The capital Greek letter sigma,
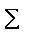 , corresponds with our S and is used to represent a
s
um. The numbers to be summed are formed according to the formula, here
, corresponds with our S and is used to represent a
s
um. The numbers to be summed are formed according to the formula, here
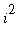 , where
, where
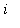 is the
index
. The
lower
and
upper limits
on the range of index values are the integers that appear below and above the
is the
index
. The
lower
and
upper limits
on the range of index values are the integers that appear below and above the
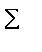 , respectively; in this example the lower index is 1 and the upper index is 10.
, respectively; in this example the lower index is 1 and the upper index is 10.
When there are many numbers to be summed, sigma notation provides a more efficient way to represent the sum. Another benefit of sigma notation is seen when one or both of the limits of summation are not explicit integers. For example, if you have 1000 spheres, how many layers could you have in a pyramid built according to the guidelines described above? To answer this question it is necessary to find the largest value of
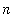 such that
such that
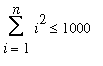 .
.
Summation Formulae and Properties
There are a few sums that will appear repeatedly in the next few lessons.
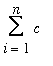 =
=
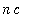
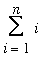 =
=
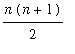
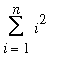 =
=
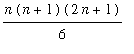
The proofs of these results are typically based on a clever rewriting of the terms of the sum or induction; these details are not important at this time.
Also, because sigma notation is another way to write a sum, all properties of sums carry over to sums represented by sigma notation. For example,
![Sum(c*a[i]+d*b[i],i = m .. n) = c*Sum(a[i],i = m .. n)+d*Sum(b[i],i = m .. n)](images/RiemannSum18.gif)
Returning to the questions posed - but not answered - in the previous section, the number of spheres in a ten layer pyramid is
| > |
s10 := Sum( i^2, i=1..10 ):
s10 = `10`*`(10+1)`*`(2*10+1)`/`6`;
`` = `10`*`(11)`*`21`/6;
`` = 385;
|
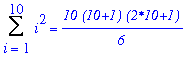
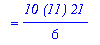
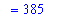
Or, letting Maple do the work:
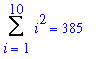
The total number of spheres needed to build a pyramid with
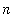 layers is
layers is
| > |
sn := Sum( i^2, i=1..n ):
sn = factor(value( sn ));
|
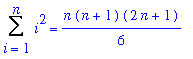
A pyramid with
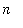 layers can be built with 1000 spheres provided
layers can be built with 1000 spheres provided
| > |
sn := Sum( i^2, i=1..n ):
q1 := sn <= 1000.:
q1;
|
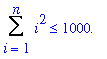
| > |
q2 := factor(value(q1)):
q2;
|
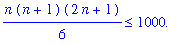
The solution to this cubic inequality is difficult to find manually, but Maple can complete this task with ease. The result is
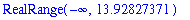
That is,
| > |
s13 := eval( sn, n=13 ):
s13 = value( s13 );
|
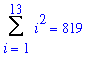
After constructing the 13-layer pyramid with 819 spheres there will be 181 spheres remaining. With the 181 spheres that remain, another pyramid could be built.
| > |
solve( value(sn)<=181., n );
|
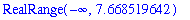
| > |
s7 := eval( sn, n=7 ):
s7 = value( s7 );
|
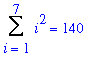
This pyramid would have 140 spheres in 7 layers. More pyramids could be made with the 41 spheres that remain: 1 4-layer pyramid with 30 spheres, 2 2-layer pyramids with 5 spheres each, and 1 1-layer pyramid.
Area Approximations by Rectangles
A fundamental mathematical problem prior to the discovery of calculus was the computation of the area of a region. The general approach to such problems is to approximate the region with a finite collection of simple regions -- typically rectangles-- and then take a limit. As was done for both limits and derivatives, our initial investigations will develop the intuitive (graphical) understanding of this idea. The
ApproximateInt
command from the
Student[Calculus1]
package will be used to create both plots and symbolic sums in sigma notation. The
ApproximateIntegration
maplet [
Maplet Viewer][
MapleNet] can be used to obtain similar results without the complications of the syntax of the
ApproximateInt
command,
Example 1: Area of a Trapezoid
Find the area of the region bounded by the graphs of
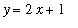 ,
,
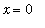 ,
,
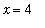 , and
, and
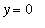 .
.
| > |
F1 := 2*x + 1:
y = F1;
a := 0;
b := 4;
|
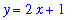
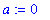
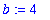
| > |
P1 := plot( F1, x=a..b, filled=true, color=pink,
title="Region for Example 1" ):
display( P1 );
|
![[Maple Plot]](images/RiemannSum39.gif)
There are a number of ways to use the fact that this region is a trapezoid to directly compute the area. The purpose of this lesson, however, is to illustrate the calculus-based approach using approximations.
Step 1: 4 subintervals
Graphical
To begin, divide the base of the region, the interval [ 0, 4 ], into 4 subintervals of length 1. On each of these subintervals, construct the tallest rectangle that fits completely under the graph. The following plot shows the full region (pink) and the four rectangles (outlined in blue).
| > |
PA4 := ApproximateInt( F1, x=a..b, partition=4, method=lower,
output=plot, boxoptions=[color=blue],
showarea=false, title="" ):
display( [P1,PA4], title="Approximate Area with 4 Rectangles" );
|
![[Maple Plot]](images/RiemannSum40.gif)
The area of the four rectangles is an approximation to the total area of the trapezoid.
Numerical
The heights of the rectangles are 1, 3, 5, and 7. Because each rectangle has base 1, the total area of the four rectangles is
1(1) + 1(3) + 1(5) + 1(7) = 1 + 3 + 5 + 7 = 16.
As a result of the fact that the graph of
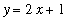 is always increasing, the tallest rectangle fitting under the graph occurs at the left endpoint of each subinterval.. The sum of the four rectangles can be written in sigma notation and evaluated using the
ApproximateInt
command from the
Student[Calculus1]
package as follows:
is always increasing, the tallest rectangle fitting under the graph occurs at the left endpoint of each subinterval.. The sum of the four rectangles can be written in sigma notation and evaluated using the
ApproximateInt
command from the
Student[Calculus1]
package as follows:
| > |
SA4 := ApproximateInt( F1, x=a..b, partition=4, method=left, output=sum ):
SA4 = value( SA4 );
|
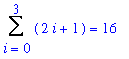
Step 2: 8 subintervals
Graphical
Divide the base of each of the four rectangles into two equal subintervals and construct rectangles on these eight subintervals as before.
| > |
PA8 := ApproximateInt( F1, x=a..b, partition=8, method=left,
output=plot, boxoptions=[color=green, thickness=2],
showarea=false, title="", functionoptions=[legend=""] ):
display( [P1, PA4, PA8], title="Approximate Area with 4 and 8 Rectangles" );
|
![[Maple Plot]](images/RiemannSum43.gif)
Notice how these eight rectangles (outlined in green) provide a better approximation to the exact area of the pink region than the four wider rectangles.
Numerical
The base of each of the eight rectangles is
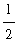 ; the heights are 1, 2, 3, 4, 5, 6, 7, and 8. Thus, the total area enclosed by these 8 rectangles is
; the heights are 1, 2, 3, 4, 5, 6, 7, and 8. Thus, the total area enclosed by these 8 rectangles is
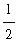 (1) +
(1) +
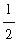 (2) +
(2) +
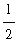 (3) +
(3) +
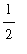 (4) +
(4) +
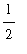 (5) +
(5) +
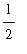 (6) +
(6) +
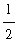 (7) +
(7) +
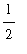 (8) =
(8) =
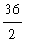 = 18.
= 18.
This sum is tedious to write. Because the pattern is so simple, it is not difficult to write the sum in sigma notation and then evaluate the sum:
| > |
SA8 := ApproximateInt( F1, x=a..b, partition=8, method=left, output=sum ):
SA8 = value( SA8 );
|
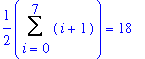
Note
Note that Maple factored the common base out of each term and that the sum could also have been written as
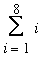 .
.
Step 3: 16 subintervals
Graphical
Once again, divide the base of each rectangle in half and construct the 16 rectangles on these subintervals as before.
| > |
PA16 := ApproximateInt( F1, x=a..b, partition=16, method=lower,
output=plot, boxoptions=[color=cyan, thickness=3],
showarea=false, title="", functionoptions=[legend=""] ):
display( [P1,PA4,PA8,PA16], title="Approximate Area with 4, 8, and 16 Rectangles" );
|
![[Maple Plot]](images/RiemannSum56.gif)
Visually, the 16 rectangles provide a better approximation that the 8 rectangles. Note that all three estimates are smaller than the actual area of the trapezoid.
Numerical
The base of each rectangle is now 1/4. The first rectangle has height 1 and each successive rectangle's height increases by 1/2; the last rectangle has height 17/2. The total area enclosed by these 16 rectangles is, in sigma notation:
| > |
SA16 := ApproximateInt( F1, x=a..b, partition=16, method=left, output=sum ):
SA16 = value( SA16 );
|
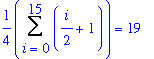
Step 4: Take it to the limit
Graphical
The subdivision process started in Steps 1-3 can be continued forever. Practially speaking, however, it is difficult to see more than 500 rectangles in a single plot. The following animation shows the lower rectangle approximation (and corresponding total area) for 4, 8, 16, 32, 64, 128, 256, and 512 rectangles.
| > |
ApproximateInt( F1, x=a..b, partition=4, method=lower,
output=animation, refinement=halve, iterations=8,
title="" );
|
![[Maple Plot]](images/RiemannSum58.gif)
Notice how the last frames very nearly completely cover the trapezoid. Because of the way the rectangles are selected, all of these approximations to the area are too small. For these reasons, and others, it is tempting to suggest that the area of this trapezoid is 20 (square units).
Analytical
The final step in this process is to perform the symbolic calculations that will show the exact area of this trapezoid. For this it is necessary to work with a general partition with n subintervals. When the left endpoint of each interval is used to form the rectangles, the total area with n subintervals is
| > |
SAn := ApproximateInt( F1, x=a..b, partition=n, method=left, output=sum ):
SAn = value( SAn );
|
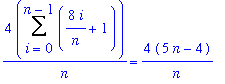
As remarked previously, each of these approximate areas is too small but converges to the true area of the trapezoid:
| > |
SA := Limit( SAn, n=infinity ):
Area[trapezoid] = SA;
`` = Limit( value( SAn ), n=infinity );
`` = value( SA );
|
![Area[trapezoid] = Limit(4/n*Sum(8*i/n+1,i = 0 .. n-1),n = infinity)](images/RiemannSum60.gif)
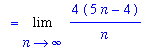
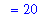
Note that if the right-hand endpoints of each subinterval are used to determine the height of the rectangle on each subinterval, then each rectangle is extends above the top of the trapezoid and the approximations tothe area are all slightly too large. But, in the limit, the value should approach the true area:
| > |
SAn2 := ApproximateInt( F1, x=a..b, partition=n, method=right, output=sum ):
SA2 := Limit( SAn2, n=infinity ):
Area[trapezoid] = SA2;
`` = Limit( value( SAn2 ), n=infinity );
`` = Limit( simplify(value( SAn2 )), n=infinity );
`` = value( SA2 );
|
![Area[trapezoid] = Limit(4/n*Sum(8*i/n+1,i = 1 .. n),n = infinity)](images/RiemannSum63.gif)
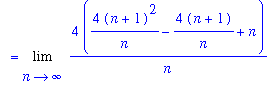
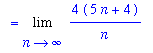
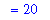
The area of this trapezoid is, in fact, 20.
Riemann Sums
Each of the sums encountered in the discussion of Area Approximation by Rectangles is a special type of sum called a Riemann sum. The importance of this observation is that appropriate limits of Riemann sums can be related to integrals and antiderivatives. But, first, let's learn a little more about Riemann sums.
Definition (Riemann Sum )
Let
-
f be a function defined on on a closed interval
![[a, b]](images/RiemannSum67.gif) .
.
-
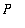 be a partition of
be a partition of
![[a, b]](images/RiemannSum69.gif) into
into
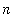 subintervals with endpoints
subintervals with endpoints
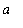 =
=
![x[0]](images/RiemannSum72.gif) <
<
![x[1]](images/RiemannSum73.gif) <
<
![x[2]](images/RiemannSum74.gif) < ... <
< ... <
![x[n-1]](images/RiemannSum75.gif) <
<
![x[n]](images/RiemannSum76.gif) =
=
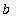 .
.
A
Riemann sum
of f on the partition
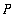 is any sum of the form
is any sum of the form
![Sum(f(conjugate(x)[i])*Delta*x[i],i = 1 .. n)](images/RiemannSum79.gif)
where, for each
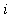 = 1, 2, ...,
= 1, 2, ...,
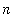 :
:
-
the width of subinterval
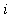 is
is
![Delta*x[i] = x[i]-x[i-1]](images/RiemannSum83.gif)
-
![conjugate(x)[i]](images/RiemannSum84.gif) is a point in subinterval
is a point in subinterval
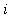 , i.e.,
, i.e.,
![x[i-1]](images/RiemannSum86.gif) <=
<=
![conjugate(x)[i]](images/RiemannSum87.gif) <=
<=
![x[i]](images/RiemannSum88.gif) .
.
Observe that the points
![conjugate(x)[i]](images/RiemannSum89.gif) can be selected by different methods in different subintervals. More typically, however, these points are selected to be the right or left endpoint of the subinterval or the location of the largest or smallest value of f on the subinterval. To emphasize this aspect of Riemann sums, return to (or reactivate) the
ApproximateIntegration
maplet [
Maplet Viewer][
MapleNet]. Let the
Function
be
x^2-x+2
with
a =
0
and
b =
2
. (Set the
Number of Partitions
to
10
.) Click the
random
button in the Riemann Sum window, then click the
Plot
button at the bottom of the maplet window. After the plot appears, click the
Plot
button again; repeat this several more times, each time recording the approximate value of the area under this curve. Click the
Compare
button. How do the approximations for other Riemann sums compare with the ones you found with randomly selected points in each subinterval? Repeat this experiment with twice as many partitions, say
20
; do not forget to use the
Compare
button to obtain a single list with several different Reimann sums. Repeat this test one more time, with the
Number of Partitions
set to
40
. Your table of values might look something like the following table; the
RiemannSumComparison
procedure (defined at the top of this worksheet) can be helpful when comparing a list of Riemann sums:
can be selected by different methods in different subintervals. More typically, however, these points are selected to be the right or left endpoint of the subinterval or the location of the largest or smallest value of f on the subinterval. To emphasize this aspect of Riemann sums, return to (or reactivate) the
ApproximateIntegration
maplet [
Maplet Viewer][
MapleNet]. Let the
Function
be
x^2-x+2
with
a =
0
and
b =
2
. (Set the
Number of Partitions
to
10
.) Click the
random
button in the Riemann Sum window, then click the
Plot
button at the bottom of the maplet window. After the plot appears, click the
Plot
button again; repeat this several more times, each time recording the approximate value of the area under this curve. Click the
Compare
button. How do the approximations for other Riemann sums compare with the ones you found with randomly selected points in each subinterval? Repeat this experiment with twice as many partitions, say
20
; do not forget to use the
Compare
button to obtain a single list with several different Reimann sums. Repeat this test one more time, with the
Number of Partitions
set to
40
. Your table of values might look something like the following table; the
RiemannSumComparison
procedure (defined at the top of this worksheet) can be helpful when comparing a list of Riemann sums:
| > |
RiemannSumComparison( x^2-x+2, 0, 3, [ 10, 20, 40 ], [lower,random,random,upper] );
|

Feel free to experiment with this command for different functions, intervals, number of partitions, and types of methods in the previous command.
You should be able to make several observations about the data presented in this matrix.:
-
all estimates fall within the values reported for the upper and lower sums for each partition size,
-
the approximations with randomly selected points change every time a new estimate is requested, (but every approximation falls within the upper and lower Riemann sums),
-
as the number of partitions increases, the upper and lower Riemann sums move closer together,
In fact, in the limit as the partition width decreases to zero, the upper and lower Riemann sums converge to the same value. Because all other Riemann sums are within the interval created by the upper and lower Riemann sums, they, too, must converge to the same limit. This limit is the definite integral of f on [ 0, 2 ]. (A precise definition of the definite integral will be provided in the
Definite Integral lesson.)
Lesson Summary
This lesson introduced several new ideas: summation notation, area approximations by rectangles, and Riemann sums and how these topics are related. Summation notation provides a shorthand notation for writing the sum of a (finite or infinite) sequence of numbers. It is important that you are comfortable with the notation and are able to identify and evaluate some simple sums. We are also able to recognize a special class of sums: Riemann sums. Riemann sums are important to the computation of the area of a region with a curved boundary.
What's Next?
The problems associated with this lesson are more conceptual than in most other lessons. A solid understanding of the fundamental concepts will be critical to understanding the remainder of this. Do not be fooled by the relatively small number of problems that ask you to compute something. In addition to the online practice sessions, you are strongly encouraged to pay close attention to the
assigned problems from the text. Complete the
online homework assignment only after you are completely comfortable with the new ideas and can explain how they are interconnected.
The first three lessons of this unit have introduced quite a few different ideas:
Antiderivatives,
Differential Equations, and
Riemann Sums.
Quiz 7 contains questions related to these lessons.
The next lesson completes the development of the
Definite Integral. This is one of the most important ideas of this course. The conceptual significance of the definite integral will be made clear in the
Fundamental Theorems of Calculus lesson. The results in this lesson show the close relationship between
Indefinite Integrals and
Definite Integrals. This connection provides methods for efficiently
Evaluating Definite Integrals.
![]() spheres.
spheres.
![[Maple Plot]](images/RiemannSum2.gif)
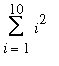 . This expression is read as ``the sum of
. This expression is read as ``the sum of
![]() squared from
squared from
![]() equals 1 to 10''. The capital Greek letter sigma,
equals 1 to 10''. The capital Greek letter sigma,
![]() , corresponds with our S and is used to represent a
s
um. The numbers to be summed are formed according to the formula, here
, corresponds with our S and is used to represent a
s
um. The numbers to be summed are formed according to the formula, here
![]() , where
, where
![]() is the
index
. The
lower
and
upper limits
on the range of index values are the integers that appear below and above the
is the
index
. The
lower
and
upper limits
on the range of index values are the integers that appear below and above the
![]() , respectively; in this example the lower index is 1 and the upper index is 10.
, respectively; in this example the lower index is 1 and the upper index is 10.
![]() such that
such that
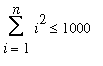 .
.
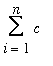 =
=
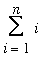 =
=
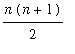
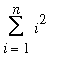 =
=
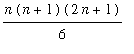
![Sum(c*a[i]+d*b[i],i = m .. n) = c*Sum(a[i],i = m .. n)+d*Sum(b[i],i = m .. n)](images/RiemannSum18.gif)
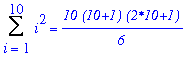
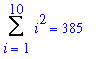
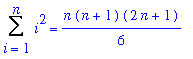
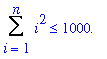
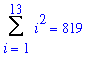
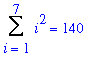
![[Maple Plot]](images/RiemannSum39.gif)
![[Maple Plot]](images/RiemannSum40.gif)
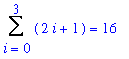
![[Maple Plot]](images/RiemannSum43.gif)
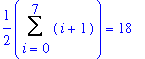
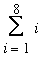 .
.
![[Maple Plot]](images/RiemannSum56.gif)
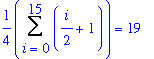
![[Maple Plot]](images/RiemannSum58.gif)
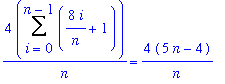
![Area[trapezoid] = Limit(4/n*Sum(8*i/n+1,i = 0 .. n-1),n = infinity)](images/RiemannSum60.gif)
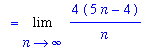
![Area[trapezoid] = Limit(4/n*Sum(8*i/n+1,i = 1 .. n),n = infinity)](images/RiemannSum63.gif)
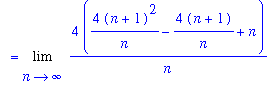
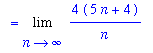
![Sum(f(conjugate(x)[i])*Delta*x[i],i = 1 .. n)](images/RiemannSum79.gif)
