DefiniteInt.mws

Definite Integrals

>    restart;
with( plots ): 

Warning, the name changecoords has been redefined

Lesson Overview

The definite integral consolidates all of the different Riemann sums introduced in the previous lesson.  The purpose of this lesson is to present and discuss the definition of the definite integral and to become familiar with the basic properties of the definite integral.  For the discussions in this lesson, the known area of geometric regions will be used to evaluate definite integrals.

Once these preliminaries are complete this unit concludes with the Fundamental Theorems of Calculus, where the relationship between definite and Indefinite Integrals (Antiderivatives) is made, and Evaluating Definite Integrals, where additional high-level techniques for evaluating definite integrals will be developed.

>   

The Definite Integral

The discussion of Riemann sums in the previous lesson considers a number of different choices of partition of the interval [ a , b  ] and of sample points (right, left, midpoint, random) within each subinterval.  The examples suggest that, in the limit as the width of the partition decreases to zero, these choices are not important.  That is, if the limit exists for one choice of partitions and sample points then it converges, with the same limit, for any choice of partition and sample points.  When the function f is positive on the interval [ a , b  ], this limit is the area between the graph of y = f(x)  and the x -axis above the interval [ a , b  ].  More generally, these limits of Riemann sums are called definite integrals .

>   

Definition ( Definite Integral )

Let

  •  f be a function defined on on a closed interval [a, b] .
  •   P  be a partition of [a, b]  into n  subintervals with endpoints

   a  = x[0]  < x[1]  < x[2]  < ... < x[n-1]  < x[n]  = b .  

  • the width of subinterval i  is Delta*x[i] = x[i]-x[i-1]  
  • the width of partition P  is Delta*x = max[i = 1 .. n]*Delta*x[i]  
  • conjugate(x)[i]  is a point in subinterval i , i.e., x[i-1]  <= conjugate(x)[i]  <= x[i]

The definite integral  of a function f over an interval [ a , b  ] is

   Int(f(x),x = a .. b) = Limit(Sum(f(conjugate(x)[i])*Delta*x[i],i = 1 .. n),Delta*x = 0,right)   

provided the limit exists.  When this definite integral exists it is said that f is (Riemann) integrable on  [ a , b  ].

>   

>   

At this point the only options for evaluating a definite integral are i) to use the definition in terms of limits and ii) to recognize the definite integral as the known area of a geometric region.  One of the most important results in calculus is that definite integrals can be evaluated using an antiderivative of the integrand.  The Fundamental Theorems of Calculus and Evaluating Definite Integrals lessons that conclude this unit contain this result and other techniques for the evaluation of definite integrals.

>   

Example 1

In the Riemann Sums lesson the left, right, and two different random Riemann sums for

>    f1 := x^2 - x + 2:
f(x) = f1;

f(x) = x^2-x+2

on the interval [ 0, 3 ]

>    a1 := 0:
b1 := 3:

all appeared to converge to the same value: 21/2.  That is,

>    Int( f1, x=a1..b1 ) = 21/2;

Int(x^2-x+2,x = 0 .. 3) = 21/2

>    plot( f1, x=a1..b1 );

[Maple Plot]

>   

Theorem 1

If f is a continuous function on the closed interval [ a , b  ], then f is Riemann integrable on [ a , b  ].

>   

>   

The class of integrable functions will be expanded later in this lesson.  But, first, let's begin to develop some properties for definite integrals.

>   

Property 1: Int(f(x),x = a .. a) = 0  

This does not require much discussion.  So long as the integrand is finite at x = a , the region will be a "rectangle" with height f(a)  and "width" a-a = 0 .  The area of this rectangle is 0.  Stated in terms of definite integrals:

   Int(f(x),x = a .. a) = 0 .  

>   

Property 2: Int(f(x),x = a .. b) = Int(f(x),x = a .. c)+Int(f(x),x = c .. b)  

Assume c  is a number between a  and b .  Geometrically, this makes intuitive sense.  If f(x)  >= 0 for all a  <= x  <= b , then the area under the graph of y = f(x)  over [ a , b  ] is the sum of the areas under the graph of y = f(x)  over [ a , c  ] and over [ c , b  ].

>    P1 := plot( f1, x=0..2, color=cyan, filled=true ):
P2 := plot( f1, x=2..3, color=pink, filled=true ):
display( P1,P2, title="Int( f(x), x=0..3 ) = Int( f(x), x=0..2 ) + Int( f(x), x=2..3 )" );

[Maple Plot]

>   

If the integrand has some negative values on [ a , b  ], then it is not possible to use area to justify this property.  Instead it is necessary to look at partitions.

>   

Let Q[n]  be a partition of [ a , c  ] into n subintervals with endpoints a  = u[0]  < u[1]  < ... < u[n-1]  < u[n]  = b  with the property that

   Limit(Sum(f(u[i])*Delta*u[i],i = 1 .. n),n = infinity) = Int(f(x),x = a .. b)   

and let R[n]  be a partition of [ c , b  ] into n subintervals with endpoints b  = v[0]  < v[1]  < ... < v[n-1]  < v[n]  = c  with the property that

   Limit(Sum(f(v[i])*Delta*v[i],i = 1 .. n),n = infinity) = Int(f(x),x = b .. c) .  

>   

The points x[0] = u[0] , x[1] = u[1] , ... x[n] = u[n] , x[n+1] = v[1] , x[n+2] = v[2] , ... , x[2*n] = v[n]  form a partition P[n] = `union`(Q[n],R[n])  of [ a, b ] into 2*n  subintervals with widths Delta*x[i] = Delta*u[i]  and Delta*x[n+i] = Delta*v[i] , for i = 1, 2, ..., n,.  Then, for each integer n ,

   Sum(f(x[i])*Delta*x[i],i = 1 .. 2*n) = Sum(f(x[i])*Delta*x[i],i = 1 .. n)+Sum(f(x[i])*Delta*x[i],i = n+1 .. 2*n)   

                   = . Sum(f(u[i])*Delta*u[i],i = 1 .. n)+Sum(f(v[i])*Delta*v[i],i = 1 .. n)   

and the linearity of limits yields

   Limit(Sum(f(x[i])*Delta*x[i],i = 1 .. 2*n),n = infinity) = Limit(Sum(f(x[i])*Delta*x[i],i = 1 .. n)+Sum(f(x[i])*Delta*x[i],i = n+1 .. 2*n),n = infinity)   

                                         = Limit(Sum(f(u[i])*Delta*u[i],i = 1 .. n),n = infinity)+Limit(Sum(f(v[i])*Delta*v[i],i = n .. n),n = infinity)   

  =   Int(f(x),x = a .. b)+Int(f(x),x = b .. c)          

>   

Now, because the original limit of Riemann sums over [ a , b  ] exists, it can be identified and written as a definite integral.  That is,

   Int(f(x),x = a .. b) = Limit(Sum(f(x[i])*Delta*x[i],i = 1 .. 2*n),n = infinity)   

                 = Int(f(x),x = a .. b)+Int(f(x),x = b .. c) .  

While this proof is valid only when a  <= c  <= b , the result is true for any value of c  for which all three integrals exist.

>   

Example 2: Piecewise Continuous Integrand

Let a be a positive constant.  Find the area of the regoin in the first quadrant bounded by the graph of

>    f2 := piecewise( x>=0 and x<a, sqrt( 2*a*x-x^2 ), x>=a and x<= 3*a, (3*a-x)/2 ):
f(x) = f2;

f(x) = PIECEWISE([(2*a*x-x^2)^(1/2), -x <= 0 and x-a < 0],[3/2*a-1/2*x, -x+a <= 0 and x-3*a <= 0])

While it is not possible for Maple to graph this region in terms of the parameter a , it can be graphed for specific values of a .  For instance, with a = 2 , the region is:

>    P3 := plot( eval(f2,a=2), x=0..6, scaling=constrained ):
P3;

[Maple Plot]

This region is clearly the union of a quarter circle and a triangle

>    P4 := plot( eval(f2,a=2), x=0..2, color=pink, filled=true ):
P5 := plot( eval(f2,a=2), x=2..6, color=cyan, filled=true ):
display( P3,P4,P5 );

[Maple Plot]

The area of the pink region is a quarter circle with radius 2.  The area of the blue region is a triangle with base 4 and height 2.  Therefore, by Property 2,

   Int(f(x),x = 0 .. 6) = Pi*2^2/4+4(2)/2  = Pi+4 .  

>   

More generally, the region consists of the union of a quarter circle with radius a  above [ 0, a  ] and a triangle with base 2*a  and height a  above [ a , 3*a  ].  Thus,

   Int(f(x),x = 0 .. 3*a) = Int(f(x),x = 0 .. a)+Int(f(x),x = a .. 3*a)   

                                        = Int(sqrt(2*x*a-x^2),x = 0 .. a)+Int((3*a-x)/2,x = a .. 3*a)   

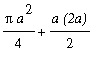
    = Pi*a^2/4+a*`(2a)`/2   

    = (Pi/4+1)*a^2 .  

>   

Theorem 2

If f is a piecewise continuous function on the interval [ a , b  ], then f is (Riemann) integrable on [ a , b  ].

Sketch of Proof

Divide the interval [ a , b  ] into a finite number of nonoverlapping intervals, I[1] , I[2] , ..., I[k] , on which f is continuous.  Then, by Theorem 1, f is integrable on each of the smaller intervals.  Property 2 tells us the sum of these definite integrals is the definite integral over [ a , b  ].  Since this definite integral exists, f must be (Riemann) integrable on the full interval, [ a , b  ].

>   

>   

Example 3: A Nonintegrable Function

Consider the function

   f(x) = PIECEWISE([1, x*` rational`],[0, x*` irrational`])   

>   

Recall that between any two rational numbers there is at least one irrational number and that between any two irrational numbers there is at least one rational number.  Due to the way rational and irrational numbers are interspersed, it is not possible to create an instructive plot of this function.  In fact, because every floating-point number representable in a computer is rational, a computer-generated plot would look like the horizontal line y = 1 .

>   

Let P[n]  be the partition of [ 0, 1 ] into n subintervals with x[i] = i/n .  Then Delta*x[i] = Delta*x  = 1/n  for all i .  Because every subinterval contains a rational number the largest value of f on the subinterval is 1.  Thus, the upper Riemann sum on P[n]  is

   U[n] = Sum(1*Delta*x[i],i = 1 .. n)  = Sum(1/n,i = 1 .. n) = 1 .  

Likewise, the smallest value on every subinterval is 0 and the lower Riemann sum of P[n]  is

   L[n] = Sum(0*Delta*x[i],i = 1 .. n)  = Sum(0,i = 1 .. n) = 0 .  

While the sequence of upper Riemann sums converges to 1 and the sequence of lower Riemann sums converges to 0, the fact that the upper and lower Riemann sums for the same function and interval do not converge to the same value means that this function is not Riemann integrable.

>   

>   

The function in Example 3 is unlike any other function encountered in this course.  It is included here only to show that there are, in fact, some functions that are not integrable.  You will not encounter another function like this in this course -- well, there might be something like this in the online homework.

>   

Property 3: Int(f(x),x = b .. a) = -Int(f(x),x = a .. b)  

By Property 2 it is known that

   Int(f(x),x = a .. a) = Int(f(x),x = a .. b)+Int(f(x),x = b .. a) .  

By Property 1 the left-hand side of this equation is 0.  Thus,

   0 = Int(f(x),x = a .. b)+Int(f(x),x = b .. a)   

and so

   Int(f(x),x = b .. a) = -Int(f(x),x = a .. b) .  

>   

Property 4: Int(r*f(x)+s*g(x),x = a .. b) = r*Int(f(x),x = a .. b)+s*Int(g(x),x = a .. b)  

Linearity of the definite integral is a direct consequence of the linearity of limits and sums:

   Int(r*f(x)+s*g(x),x = a .. b) = Limit(Sum(r*f(x[i])+s*g(x[i]),i = 1 .. n),n = infinity)                              

                     = Limit(r*Sum(f(x[i]),i = 1 .. n)+s*Sum(g(x[i]),i = 1 .. n),n = infinity)   

                                 = r*Limit(Sum(f(x[i]),i = 1 .. n),n = infinity)+s*Limit(Sum(g(x[i]),i = 1 .. n),n = infinity)   

  = r*Int(f(x),x = a .. b)+s*Int(g(x),x = a .. b) .   

>   

Example 4

In Example1 it was determined that

   Int(x^2-x+2,x = 0 .. 3) = 21/2 .  

Use the properties of definite integrals to determine Int(x^2,x = 0 .. 3) .

>   

Linearity of the definite integral, Property 4, allows us to write

   Int(x^2-x+2,x = 0 .. 3) = Int(x^2,x = 0 .. 3)+Int(-x,x = 0 .. 3)+Int(2,x = 0 .. 3)   

                               = Int(x^2,x = 0 .. 3)-Int(x,x = 0 .. 3)+2*Int(1,x = 0 .. 3)   

The definite integral on the left is known (from Example 1).  The second and third integrals on the right hand side can be determined by geometry:

  Int(x,x = 0 .. 3) = 9/2  

>    plot( x, x=0..3, color= pink, filled=true );

[Maple Plot]

The area of the right triangle with base3  and height 3 is

   Int(x,x = 0 .. 3)  = 1/2  (3) (3) = 9/2 .  

>   

  Int(1,x = 0 .. 3) = 3  

>    plot( 1, x=0..3, color=cyan, filled=true, view=[DEFAULT,0..3] );

[Maple Plot]

The area of the rectangle with base 3 and height 1 is

   Int(1,x = 0 .. 3)  = 3 ( 1 ) = 3.  

>   

Therefore,

   Int(x^2,x = 0 .. 3) = Int(x^2-x+2,x = 0 .. 3)+Int(x,x = 0 .. 3)-2*Int(1,x = 0 .. 3)   

    = 21/2+9/2-2(3)                           

   = 9.                                              

>   

>   

Lesson Summary

One of the most important facts to take away from this lesson is the knowledge that limits of Riemann sums are definite integrals.  In most of the applications of integration considered in Unit 5, the geometric or physical principles will produce a limit of a Riemann sum.  The translation of this limit to a definite integral will facilitate the computation of this quantity.

To summarize this lesson, recall the definition of the definite integral

   Int(f(x),x = a .. b) = Limit(Sum(f(conjugate(x)[i])*Delta*x[i],i = 1 .. n),Delta*x = 0,right)   

While not every function is (Riemann) integrable, every piecewise continuous function is integrable.  On intervals where the integrand is positive, the definite integral is the area under the curve.  On intervals where the integrand is negative, the definite integral is the negative of the area between the curve and the x -axis.  Other properties of the definite integral include

   Int(f(x),x = a .. a) = 0   

   Int(f(x),x = b .. a) = -Int(f(x),x = a .. b)   

   Int(f(x),x = a .. b) = Int(f(x),x = a .. c)+Int(f(x),x = c .. b)   

   Int(r*f(x)+s*g(x),x = a .. b) = r*Int(f(x),x = a .. b)+s*Int(g(x),x = a .. b)   

What's Next?

Now that you have completed this lesson, you should practice applying the properties of definite integrals, including evaluation using known areas, with the online homework assignment.  Note there are practice sessions for specific topics, a general practice session for problems related to this lesson, and a graded homework assignment.  Work enough practice problems to master these concepts, then complete the online homework assignment and the assigned problems from the text.

The next lesson presents the Fundamental Theorems of Calculus.  The first of these results shows that it is easy to differentiate functions defined in terms of a definite integral.  The second fundamental theorem states that a definite integral can be evaluated in terms of an antiderivative of the integrand.

>   

>   

>