DerivImplicit.mws
Implicit Differentiation
| > |
restart;
with( plots ):
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Lesson Overview
Many interesting curves cannot be given in an
explicit form
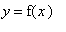
but can be given in
implicit form
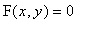 .
.
We know the slope of the tangent line to a curve at a point is
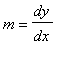 and are now comfortable finding
and are now comfortable finding
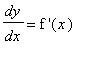 for explicit functions. Implicit differentiation is a technique that can be used to find
for explicit functions. Implicit differentiation is a technique that can be used to find
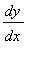 when the function is given implicitly.
when the function is given implicitly.
As this is really an application of the derivative, this lesson consists primarily of examples. The first example looks at a circle from both an explicit and an implicit formulation. The second example looks at a truly implicit function, the Folium of Descartes. The last example extends the Power Rule to all rational exponents.
The
TangentLinePlot
maplet [
Maplet Viewer][
MapleNet] can be used to assist with the visualization of tangent lines to the graph of an implicitly defined function.
Example 1: Tangent Lines for a Circle
The circle centered at the origin with radius 3 can be described as the set of all points that satisfy
| > |
q1 := x^2 + y^2 = 9:
q1;
|
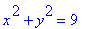
Let
 be a number with -3 <
be a number with -3 <
 < 3. Because both
< 3. Because both
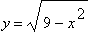 and
and
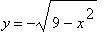 are on the graph of the circle this is not a function.
are on the graph of the circle this is not a function.
| > |
implicitplot( q1, x=-4..4, y=-4..4, title="The circle x^2+y^2=9" );
|
![[Maple Plot]](images/DerivImplicit11.gif)
To find the slope of the tangent line to the circle at a point (
 ,
,
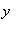 ) on the circle, requires us to find
) on the circle, requires us to find
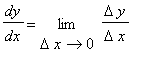 . The idea behind implicit differentiation is to think of the equation of the circle implicitly defining
. The idea behind implicit differentiation is to think of the equation of the circle implicitly defining
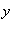 as a function of
as a function of
 . That means we need to replace all occurrences of y with y(
. That means we need to replace all occurrences of y with y(
 ):
):
| > |
yimpl := y=y(x):
yexpl := y(x)=y:
q2 := eval( q1, yimpl );
|
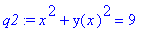
Now, if both sides of the equation are differentiated with respect to
 :
:
| > |
q3 := diff( q2, x ):
q3;
|
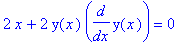
Note the use of the
Chain Rule to compute
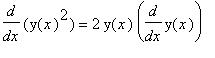 .
.
It is now a simple matter to solve for the derivative
| > |
q4 := isolate( q3, diff(y(x),x) ):
q4;
|
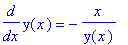
To put this result back in a form consistent with the original equation, replace all occurrences of
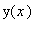 with
with
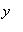 :
:
| > |
q5 := dy/dx = eval( rhs(q4), yexpl );
|
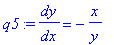
For example, the slope of the tangent line to this circle at the point ( 2,
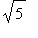 ) is
) is
| > |
eval( q5, [x=2,y=sqrt(5)] );
|
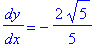
while at the point ( 2,
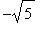 ) the slope of the tangent line to the circle is
) the slope of the tangent line to the circle is
| > |
eval( q5, [x=2,y=-sqrt(5)] );
|
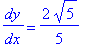
What other methods could we use to find these slopes?
The top and bottom of the circle are, separately, graphs of functions:
| > |
eq[top] := sqrt( 9 - x^2 ):
eq[bot] := -sqrt( 9 - x^2 ):
y[top] = eq[top];
y[bot] = eq[bot];
|
![y[top] = (9-x^2)^(1/2)](images/DerivImplicit30.gif)
![y[bot] = -(9-x^2)^(1/2)](images/DerivImplicit31.gif)
The slope at points on the top or bottom half of the plot can be found by differentiating these expressions. Unfortunately, we do not yet know how to differentiate the square root function. (At present the Power Rule only applies when the exponent is an integer.) But, letting Maple compute these derivatives for us, the slope of the tangent line at a point on the top half of the circle is found to be
| > |
d1 := diff( eq[top], x ):
dy/dx = d1;
|
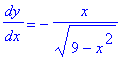
The correctness of this result can be checked by using the general formula for the slope of the tangent line and the equation for the top of the circle:
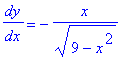
Likewise, the slope of the tangent line at a point on the bottom half of the circle is
| > |
d2 := diff( eq[bot], x ):
dy/dx = d2;
|
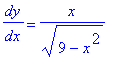
which agrees with the result from implicit differentiation:
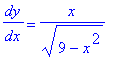
The formula for
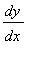 obtained above is defined only if
obtained above is defined only if
 . This makes sense because
. This makes sense because
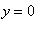 when
when
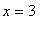 or
or
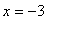 and at these points the tangent lines are vertical. These features, together with the two tangent lines to the circle at points with
and at these points the tangent lines are vertical. These features, together with the two tangent lines to the circle at points with
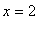 , are evident in the following plot.
, are evident in the following plot.
| > |
p1 := Tangent( eq[top], x=2, -4..4, output=plot,
functionoptions=[color=red, legend=["Top of circle"]],
tangentoptions=[color=gold,legend="Tangent to top of circle at x=2"] ):
p2 := Tangent( eq[bot], x=2, -4..4, output=plot,
functionoptions=[color=blue, legend=["Bottom of circle"]],
tangentoptions=[color=green,legend="Tangent to bottom of circle at x=2"] ):
display( [p1,p2], view=[-4..4,-4..4], title="The two tangent lines\n at x=2 for the circle\n x^2+y^2=9" );
|
![[Maple Plot]](images/DerivImplicit42.gif)
Example 2: Folium of Descartes
The general form for the Foliumm of Descartes is the implicit equation
| > |
r1 := x^3 + y^3 = 3*a*x*y;
|
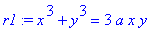
where
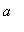 is a parameter.
is a parameter.
Visualizing the Folium of Descartes
Before analyzing these curves it will help to have an idea what these curves look like. The following animation shows plots of the Folium of Descartes for integer values of
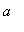 from -3 to 3.
from -3 to 3.
| > |
Pfd := [seq( implicitplot( r1, x=-6..6, y=-6..6, numpoints=2000,
title=sprintf("Folium of Descartes: a=%a",a) ),
a=-3..3 )]:
|
| > |
display( Pfd, insequence=true );
|
![[Maple Plot]](images/DerivImplicit46.gif)
For
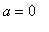 the Folium degenerates to the line
the Folium degenerates to the line
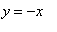 . For all
. For all
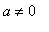 the curves are more interesting. In particular, there are regions where there are three points on the curve for a single value of
the curves are more interesting. In particular, there are regions where there are three points on the curve for a single value of
 . (This is to be expected because every cubic equation with real-valued coefficients has three real or complex roots --- and complex roots appear in conjugate pairs.)
. (This is to be expected because every cubic equation with real-valued coefficients has three real or complex roots --- and complex roots appear in conjugate pairs.)
Finding Slope by Implicit Differentiation
Implicit differentiation will be used to find the slope of the tangent line at each point on the Folium of Descartes.
| > |
r2 := eval( r1, yimpl ):
r2;
|
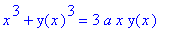
| > |
r3 := diff( r2, x ):
r3;
|
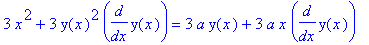
| > |
r4 := simplify(isolate( r3, diff(y(x),x) )):
r4;
|
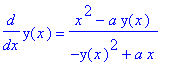
| > |
r5 := dy/dx = eval(rhs(r4),yexpl):
r5;
|
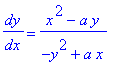
Points on Curve with Horizontal Tangents
This information can be used to identify some special points on these curves. For example, the tangent line to the curve is horizontal at points on the curve where the slope is zero, i.e., points (
 ,
,
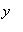 ) that satisfy both
) that satisfy both
| > |
r1;
r6 := numer( rhs(r5) ) = 0:
r6;
|
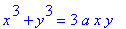
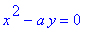
Maple reports the solutions to this pair of equations as
| > |
r7 := [solve( {r1,r6}, {x,y} )];
|
![r7 := [{y = 0, x = 0}, {y = RootOf(_Z^3-2,label = _L1)^2*a, x = RootOf(_Z^3-2,label = _L1)*a}]](images/DerivImplicit59.gif)
The
RootOf
notation is Maple's way of concisely listing all real and complex roots of a polynomial. We can force the expansion to full solutions with the
allvalues
command:
| > |
r8 := map(allvalues,r7);
|
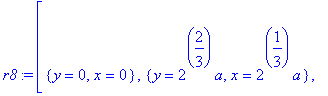
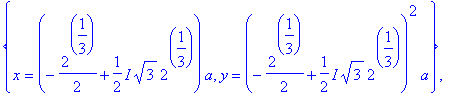
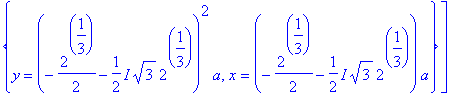
Only the real-valued solutions are of interest to us so we
remove
all solutions that have an imaginary part:
| > |
r9 := remove( has, evalc(r8), I );
|
![r9 := [{y = 0, x = 0}, {y = 2^(2/3)*a, x = 2^(1/3)*a}]](images/DerivImplicit63.gif)
This leaves, for each value of
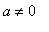 , two points with horizontal tangents:
, two points with horizontal tangents:
| > |
seq( eval( [x,y], S ), S=r9 );
|
![[0, 0], [2^(1/3)*a, 2^(2/3)*a]](images/DerivImplicit65.gif)
Points on Curve with Vertical Tangents
By the same reasoning, the slope of the tangent line to the curve is undefined at points that satisfy the two conditions
| > |
r1;
r10 := denom(rhs(r5)) = 0:
r10;
|
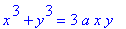
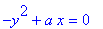
The real-valued solutions to this system are found to be:
| > |
r11 := [solve( {r1,r10}, {x,y} )]:
|
| > |
r12 := map(allvalues,r11):
|
| > |
r13 := remove( has, evalc(r12), I ):
|
| > |
seq( eval( [x,y], S ), S=r13 );
|
![[0, 0], [2^(2/3)*a, 2^(1/3)*a]](images/DerivImplicit68.gif)
Note that the origin has both a horizontal and a vertical tangent line and that the other points are symmetric about the line
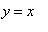 . (A closer look at the original equation and the formula for the slope explains why this - and other symmetries - are to be expected.).
. (A closer look at the original equation and the formula for the slope explains why this - and other symmetries - are to be expected.).
Points on Curve with
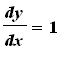
Points where the slope of the tangent line is 1 are solutions to
| > |
r1;
r14 := rhs(r5) = 1:
r14;
|
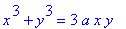
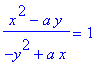
The real-valued solutions to this system are found to be:
| > |
r15 := [solve( {r1,r14}, {x,y} )]:
|
| > |
r16 := map(allvalues,r15):
|
| > |
r17 := remove( has, evalc(r16), I ):
|
| > |
seq( eval( [x,y], S ), S=r17 );
|
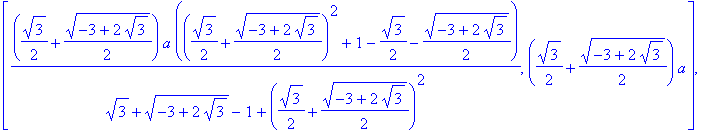
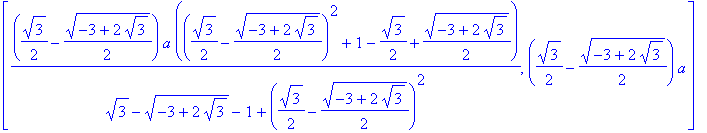
or, with floating-point approximations to the square roots
| > |
seq( eval( [x,y], evalf(S) ), S=r17 );
|
![[.5254003850*a, 1.206650424*a], [1.206650423*a, .5254003844*a]](images/DerivImplicit75.gif)
Again, note the symmetry in these solutions. Note also that these solutions are not correct for
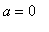 . That there are no points on the graph with slope 1 when
. That there are no points on the graph with slope 1 when
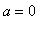 can be seen from the frame in the animation with
can be seen from the frame in the animation with
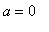 as well as from Maple's response to the following command.
as well as from Maple's response to the following command.
| > |
[solve( eval( {r1,r14}, a=0 ), {x,y} )];
|
![[]](images/DerivImplicit79.gif)
Concluding Comment: Explicit form for Folium of Descartes
At the beginning of this example it was implied that it is not possible to find an explicit representation for the Folium of Descartes. While it is true that each Folium is not the graph of a function, it is possible to find an explicit formula for each segment of the curve.
| > |
r18 := [solve( r1, {y} )]:
for S in r18 do
print( "***********************************************************************" );
op(S)
end do;
|

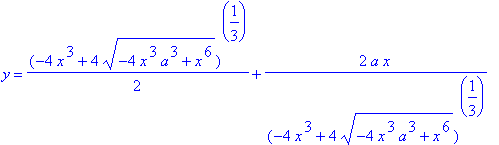

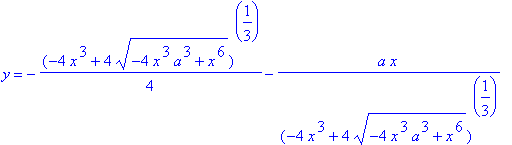
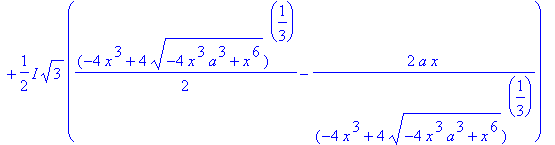

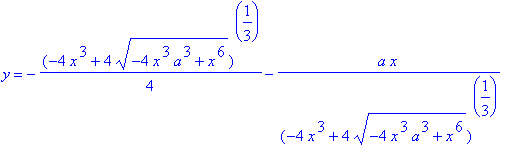
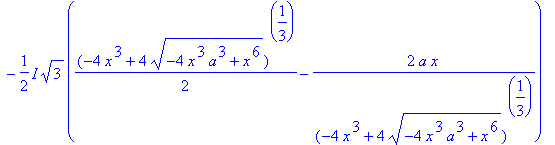
The first of the three solutions is always real-valued. The other two solutions are either real-valued or complex conjugates; when they are real-valued the Folium has three points for a single value of
 . and when they are complex conjugates there is only one point on the curve for each value of
. and when they are complex conjugates there is only one point on the curve for each value of
 ; and at the transition between these states -- the unique value of
; and at the transition between these states -- the unique value of
 with two point on the curve -- these two solutions reduce to a single repeated solution.
with two point on the curve -- these two solutions reduce to a single repeated solution.
Even if we could decide which of these three formulae to use, the derivatives would be prohibitively complicated. By comparison, these computation by implicit differentiation was almost effortless.
Example 3: The Power Rule for Rational Exponents
In Example 1 we were unable to find the slope of the tangent line to a point on the top or bottom of a circle because we did not know how to differentiate the square root function. While we could have derived this result for the square root function using the definition of the derivative, it is much more efficient and useful to handle all rational exponents simultaneously. In this example implicit differentiation will be used to show the Power Rule applies for all rational exponents. That is, if
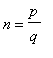 with
with
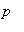 and
and
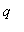 integers and
integers and
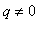 , then
, then
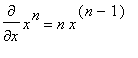 .
.
The key is to convert the explicit form
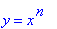
to the implicit representation with integer exponents
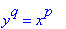
To prepare for implicit differentiation, remind ourselves (and Maple) that
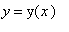 :
:
| > |
s3 := eval( s2, yimpl ):
s3;
|
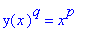
Differentiation of both sides of the equation with respect to
 yields
yields
| > |
s4 := diff( s3, x ):
s4;
|
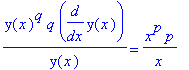
Thus,
| > |
s5 := isolate( s4, diff( y(x), x ) ):
s6 := dy/dx = simplify( eval(rhs(s5),yexpl) ) assuming p::integer, q::integer;
|
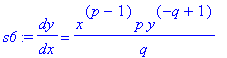
We would like to express this derivative explicitly in terms of
 . The explicit relationship
. The explicit relationship
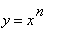 with
with
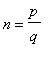 (so
(so
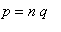 ) allow the derivative to be rewritten as
) allow the derivative to be rewritten as
| > |
qs := simplify( eval( s6, [s1,p=n*q] ) ) assuming q::integer:
qs;
|
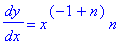
This concludes the proof that the Power Rule applies for all rational exponents.
Lesson Summary
Given an implicitly defined function,
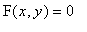 , implicit differentiation is a technique for finding the slope of the tangent line to the curve,
, implicit differentiation is a technique for finding the slope of the tangent line to the curve,
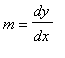 . The key to successfully using implicit differentiation is to remember that one variable is implicitly defined in terms of the other, usually
. The key to successfully using implicit differentiation is to remember that one variable is implicitly defined in terms of the other, usually
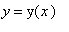 , and that differentiation of any term involving
, and that differentiation of any term involving
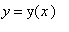 with respect to
with respect to
 will automatically involve the
Chain Rule.
will automatically involve the
Chain Rule.
An expression for
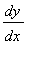 obtained by implicit differentiation will typically involve both
obtained by implicit differentiation will typically involve both
 and
and
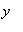 . Examples 1 and 2 demonstrate how this form for the derivative can be used effectively. The final example extends the Power Rule from integer to rational exponents. Implicit differentiation will be used in the
Related Rates lesson.
. Examples 1 and 2 demonstrate how this form for the derivative can be used effectively. The final example extends the Power Rule from integer to rational exponents. Implicit differentiation will be used in the
Related Rates lesson.
What's Next?
The
online homework assignment includes a collection of practice problems that have been formulated to further your ability to successfully apply implicit differentiation. After you are comfortable with implicit differentiation, complete the
textbook homework assignment related to this lesson.
After you finish all homework, and review the lessons in this unit, take
Quiz 2 for Unit 2.
This concludes
Unit 2. You now know all of the techniques needed to differentiate a large class of functions. You should also understand the connection between the derivative, (instantaneous) rates of change, and the slope of a tangent line to a curve. In
Unit 3 the ideas introduced in this unit will be applied to a number of different applications.
![]()
![]() .
.
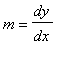 and are now comfortable finding
and are now comfortable finding
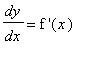 for explicit functions. Implicit differentiation is a technique that can be used to find
for explicit functions. Implicit differentiation is a technique that can be used to find
![]() when the function is given implicitly.
when the function is given implicitly.
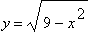 and
and
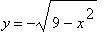 are on the graph of the circle this is not a function.
are on the graph of the circle this is not a function.
![[Maple Plot]](images/DerivImplicit11.gif)
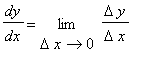 . The idea behind implicit differentiation is to think of the equation of the circle implicitly defining
. The idea behind implicit differentiation is to think of the equation of the circle implicitly defining
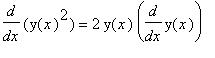 .
.
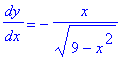
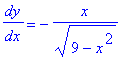
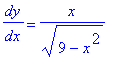
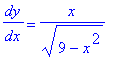
![[Maple Plot]](images/DerivImplicit42.gif)
![[Maple Plot]](images/DerivImplicit46.gif)
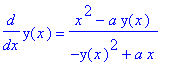
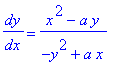
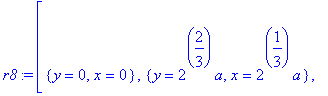
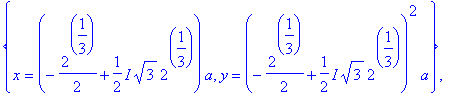
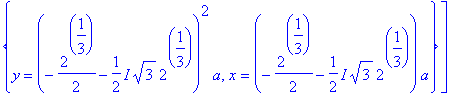
![r9 := [{y = 0, x = 0}, {y = 2^(2/3)*a, x = 2^(1/3)*a}]](images/DerivImplicit63.gif)
![[0, 0], [2^(1/3)*a, 2^(2/3)*a]](images/DerivImplicit65.gif)
![[0, 0], [2^(2/3)*a, 2^(1/3)*a]](images/DerivImplicit68.gif)
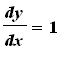
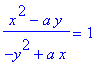
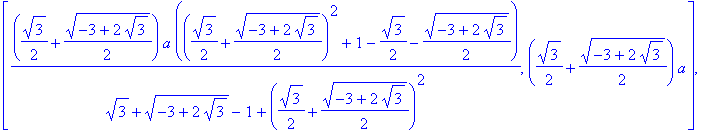
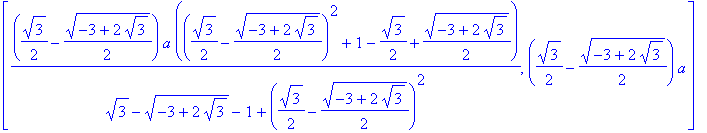
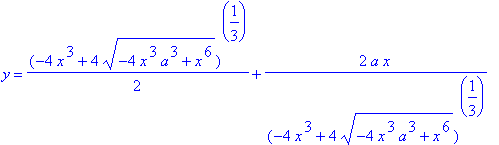
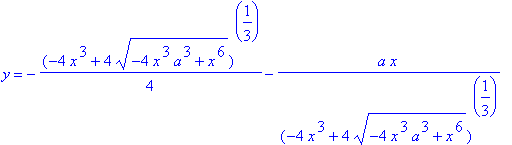
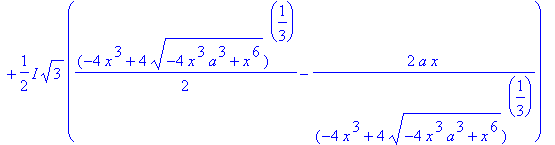
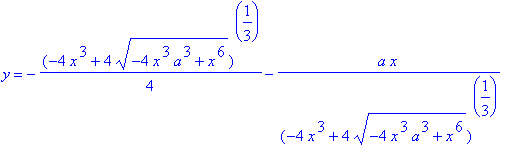
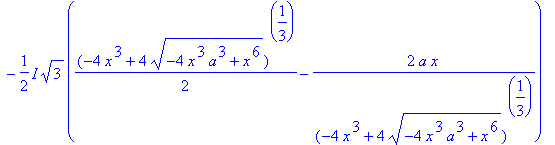
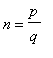 with
with
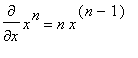 .
.
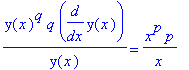
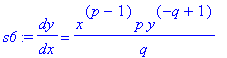
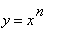 with
with
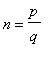 (so
(so
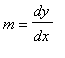 . The key to successfully using implicit differentiation is to remember that one variable is implicitly defined in terms of the other, usually
. The key to successfully using implicit differentiation is to remember that one variable is implicitly defined in terms of the other, usually