Derivative as Slope of Tangent Line
Given the graph of a function,
![]() , and a point on the graph, (
, and a point on the graph, (
![]() ,
,
![]() ), it is usually fairly easy to visually identify the tangent line to the graph at the point.
), it is usually fairly easy to visually identify the tangent line to the graph at the point.
Example 1 - Tangent Line by Zooming
Consider the graph of the function
| > | f1 := 3*x^3+9*x^2-7: f(x) = f1; |
![]()
at the point (1, 5 ).
| > | x1 := 1: y1 := eval( f1, x=x1 ): |
The graph of the function on the interval [ -3, 2 ] and the point confirm that this point is on the graph.
| > | h_list := [seq( 2^(3-i), i=1..10 )]: P1 := [ seq( Tangent( f1, x=x1, x1-h..x1+h/4, output=plot, showtangent=false, title=sprintf("Graph of y=%a on [%6.3f,%6.3f]", f1, x1-h, x1+h/4), view=[x1-h..x1+h/4,DEFAULT] ), h=h_list )]: P1[1]; |
![[Maple Plot]](images/DerivConcept5.gif)
Now, look at the graph of the function over shorter and shorter intervals around
![]() , that is, zoom in on the point ( 1, 5 ) on the graph.
, that is, zoom in on the point ( 1, 5 ) on the graph.
| > | for i from 2 to nops(P1) do P1[i]; end do; |
![[Maple Plot]](images/DerivConcept7.gif)
![[Maple Plot]](images/DerivConcept8.gif)
![[Maple Plot]](images/DerivConcept9.gif)
![[Maple Plot]](images/DerivConcept10.gif)
![[Maple Plot]](images/DerivConcept11.gif)
![[Maple Plot]](images/DerivConcept12.gif)
![[Maple Plot]](images/DerivConcept13.gif)
![[Maple Plot]](images/DerivConcept14.gif)
![[Maple Plot]](images/DerivConcept15.gif)
Notice that the graph of the function becomes straighter each time the viewing interval is cut in half. In the last few views the function appears to be a straight line. When this happens, the straight line that appears is the tangent line to the graph of the function at the point. This straightening of the graph of the function is even more apparent when tangent line is included in the plots.
| > | P1t := [ seq( Tangent( f1, x=x1, x1-h..x1+h/4, output=plot, showtangent=true, title=sprintf("Graph of y=%a on [%6.3f,%6.3f]", f1, x1-h, x1+h/4), view=[x1-h..x1+h/4,DEFAULT] ), h=h_list )]: for i from 1 to nops(P1t) do P1t[i]; end do; |
![[Maple Plot]](images/DerivConcept16.gif)
![[Maple Plot]](images/DerivConcept17.gif)
![[Maple Plot]](images/DerivConcept18.gif)
![[Maple Plot]](images/DerivConcept19.gif)
![[Maple Plot]](images/DerivConcept20.gif)
![[Maple Plot]](images/DerivConcept21.gif)
![[Maple Plot]](images/DerivConcept22.gif)
![[Maple Plot]](images/DerivConcept23.gif)
![[Maple Plot]](images/DerivConcept24.gif)
![[Maple Plot]](images/DerivConcept25.gif)
The derivative of a function at a point exists when the graph of the function has a tangent line at that point. The value of the derivative at this point is the slope of the tangent line.
In this case the equation of the tangent line to the graph of
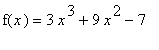 at the point ( 1, 5 ) is
at the point ( 1, 5 ) is
| > | y = Tangent( f1, x=x1, output=line ); |
![]()
so the slope of the tangent line is
| > | m = Tangent( f1, x=x1, output=slope ); |
![]()
| > |
Note: Why the zooming wasn't done with display
If the above sequence of plots is rendered with Maple's display command, the viewing window is set once and does not change from frame to frame.
| > | display( P1, insequence=true ); |
![[Maple Plot]](images/DerivConcept29.gif)
While the smaller pieces of the plot that can be seen do appear to straighten out, this is harder to conclude and much less convincing.
| > |
| > |
Example 2 - Corners
Consider the graph of the function
| > | f2 := sqrt(abs(x^2-4)+9): f(x) = f2; |
![]()
at the point ( 2, 3 ):
| > | x2 := 2: y2 := eval( f2, x=x2 ): |
| > |
The graph of the function on the interval [ -3, 7 ] and the point confirm that this point is on the graph.
| > | myTangent( f2, x=x2, -3..7, view=[DEFAULT, 0..7] ); |
![[Maple Plot]](images/DerivConcept31.gif)
Zooming in on the portion of the graph near ( 2, 3 ) leads to the plots
| > | P2 := [ seq( myTangent( f2, x=x2, x2-h..x2+h ), h=h_list ) ]: for i from 1 to nops(P2) do P2[i]; end do; |
![[Maple Plot]](images/DerivConcept32.gif)
![[Maple Plot]](images/DerivConcept33.gif)
![[Maple Plot]](images/DerivConcept34.gif)
![[Maple Plot]](images/DerivConcept35.gif)
![[Maple Plot]](images/DerivConcept36.gif)
![[Maple Plot]](images/DerivConcept37.gif)
![[Maple Plot]](images/DerivConcept38.gif)
![[Maple Plot]](images/DerivConcept39.gif)
![[Maple Plot]](images/DerivConcept40.gif)
![[Maple Plot]](images/DerivConcept41.gif)
Notice that the graph of the function has a very pronounced corner that does not disappear as the viewing window becomes smaller and smaller. At no pont will the function appear to be a (single) straight line through the point ( 2, 3 ).
The fact that there is a corner in the graph of
![]() at the point ( 2, 3 ) means there is no tangent line to this function at
at the point ( 2, 3 ) means there is no tangent line to this function at
![]() ; this function is not differentiable at
; this function is not differentiable at
![]() . This conclusion is confirmed with the
Tangent
command as follows:
. This conclusion is confirmed with the
Tangent
command as follows:
| > | Tangent( f2, x=x2 ); |
Error, (in Student:-Calculus1:-Tangent) the slope is not defied at the point `x` = 2
Example 3 - Jumps and Cusps
In addition to a corner, derivatives do not exist when the graph has a cusp or a jump at the point in question. Jumps are problematic because the tangent line does not have any jumps and so it is impossible to find a single straight line that approximates the graph of
![]() on both sides of the point.
on both sides of the point.
| > | f3a := piecewise( x<1, 1, x>1, 2 ): f(x) = f3a; |
![f(x) = PIECEWISE([1, x < 1],[2, 1 < x])](images/DerivConcept46.gif)
| > | x3a := 1: |
| > | myTangent( f3a, x=1, -1..3 ); |
![[Maple Plot]](images/DerivConcept47.gif)
| > | P3a := [ seq( myTangent( f3a, x=x3a, x3a-h..x3a+h ), h=h_list ) ]: for i from 1 to nops(P3a) do P3a[i]; end do; |
![[Maple Plot]](images/DerivConcept48.gif)
![[Maple Plot]](images/DerivConcept49.gif)
![[Maple Plot]](images/DerivConcept50.gif)
![[Maple Plot]](images/DerivConcept51.gif)
![[Maple Plot]](images/DerivConcept52.gif)
![[Maple Plot]](images/DerivConcept53.gif)
![[Maple Plot]](images/DerivConcept54.gif)
![[Maple Plot]](images/DerivConcept55.gif)
![[Maple Plot]](images/DerivConcept56.gif)
![[Maple Plot]](images/DerivConcept57.gif)
An example with a cusp is.
| > | f3b := abs(x)^(1/3): `f`(x) = f3b; |
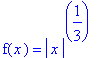
at the point ( 0, 0 ):
| > | x3b := 0: y3b := eval( f3b, x=x3b ): |
| > | myTangent( f3b, x=x3b, -3..7, view=[-3..7,0..2] ); |
![[Maple Plot]](images/DerivConcept59.gif)
While there certainly appears to be a sharp point (cusp) at the origin, it is still prudent to zoom in on this point.
| > | P3b := [ seq( myTangent( f3b, x=x3b, x3b-h..x3b+h ), h=h_list ) ]: for i from 1 to nops(P3b) do P3b[i]; end do; |
![[Maple Plot]](images/DerivConcept60.gif)
![[Maple Plot]](images/DerivConcept61.gif)
![[Maple Plot]](images/DerivConcept62.gif)
![[Maple Plot]](images/DerivConcept63.gif)
![[Maple Plot]](images/DerivConcept64.gif)
![[Maple Plot]](images/DerivConcept65.gif)
![[Maple Plot]](images/DerivConcept66.gif)
![[Maple Plot]](images/DerivConcept67.gif)
![[Maple Plot]](images/DerivConcept68.gif)
![[Maple Plot]](images/DerivConcept69.gif)
| > |
Corners, cusps, and jumps are the pictures you should have in mind when you think about a function that does not have a derivative.
- The function is (x^3-5)*(x^2-1)/(x^2+1) and we are interested in the tangent line at 2.
- Set the parameters to h= 2 and n= 20.
- In the Display Options panel, be sure all four (4) check boxes are checked and the viewing window is set to x= -2 .. 4, y= -20 .. 50.
- Click the Plot button.
- Click the Animate button.
- Use the Play , Stop , and Pause buttons to control the animation.
Example 4 - Tangent Line as Limit of Secant Lines
Note that the zooming process is a limit as the viewing window size decreases to zero. An alternate way of looking at tangent lines is to define
![`tangent line to y=f(x) at (x[1],f(x[1]))` = limit(`secant line to y=f(x) through (x[1],f(x[1])) and (x[2],f(x[2])`,x[2] = x[1])](images/DerivConcept70.gif)
Consider the function
| > | f := (x^3-5)*(x^2-1)/(x^2+1): 'f'(x) = f; |
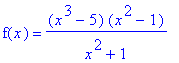
at the point with
![]() :
:
| > | x1 := 2; y1 := eval( f, x=x1 ); |
![]()
![]()
The graph of the function and the point ( 2,
![]() ) suggests that there should be a tangent line at this point.
) suggests that there should be a tangent line at this point.
| > | myTangent( f, x=x1, -2..3 ); |
![[Maple Plot]](images/DerivConcept76.gif)
We could find the tangent line by zooming. The equation of this tangent line is
| > | y = Tangent( f, x=x1, output=line ); |
![]()
Let's see if we can duplicate this result as the limit of secant lines. To begin, initalize the TangentandSecant maplet [ Maplet Viewer][ MapleNet].
The graphic panel will display a graph of the function (in red), a sequence of 20 (blue) secant lines through ( 2,
![]() ) and a second point starting at
) and a second point starting at
![]() and moving towards
and moving towards
![]() in steps of -0.1. Clearly, the secant lines converge to the tangent line (in green) as the second point slides back towards
in steps of -0.1. Clearly, the secant lines converge to the tangent line (in green) as the second point slides back towards
![]() .
.
The convergence can be animated:
The slope of each secant line is listed in the Slopes of Secant Lines panel. Observe that these values decrease from more than 25 down to 8.86. The maplet reports the slope of the tangent line to be 8.16. To obtain even better approximations to the slope of the tangent line, increase the n parameter.
To conclude, note that the slope reported from the zooming process and the
Tangent
command is
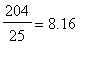 .
.
| > |
The point of these examples is that the tangent line is the straight line that appears when we zoom in on the graph of the function at a single point. The same line can be obtained as the limit of secant lines.
When the graph of a function f has a tangent line at a point (
![]() ,
,
![]() ), the slope of that tangent line is the
derivative of
f
at
), the slope of that tangent line is the
derivative of
f
at
![]() . This derivative can be written in a number of ways, including:
. This derivative can be written in a number of ways, including:
![]() =
=
![]() =
=
![]() =
=
![]() =
=
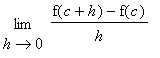
![(s(t[2])-s(t[1]))/(t[2]-t[1])](images/DerivConcept96.gif) .
.
![limit(v[avg],t[2] = t[1])](images/DerivConcept108.gif) =
=
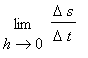 =
=
![limit((s(t[2])-s(t[1]))/(t[2]-t[1]),t[2] = t[1])](images/DerivConcept110.gif) .
.
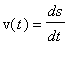 and
and
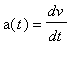 =
=
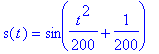
![[Maple Plot]](images/DerivConcept117.gif)
![v(t[1]) = limit((s(t[2])-s(t[1]))/(t[2]-t[1]),t[2] = t[1])](images/DerivConcept121.gif) .
.
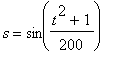 at
at
![[Maple Plot]](images/DerivConcept124.gif)