Shifting and Scaling the Graph of a Function
Calculus I Lab -- Fall 2002
prepared by
Douglas B. Meade
Department of Mathematics
University of South Carolina
Columbia, SC 29208
E-mail: meade@math.sc.edu
26 August 2002
adapted from
Technology Project 2.1 in Calculus, Varberg, Purcell, Rigdon, 8th edition, 2000, Prentice-Hall
Purpose
The ability to recognize graphs of related functions can be very useful. For example, when a collection of data points are plotted a slope, period, amplitude, or other feature might become apparent. Armed with this knowledge, it can be possible to come up with a good functional approximation to the data.
In the first part of this project we will be focused on the connections between the graph of a given function,
 , and the graphs of the related functions
, and the graphs of the related functions
 ,
,
 ,
,
 , and
, and
 . In the second part of the project we will examine the graphical properties of even and odd functions.
. In the second part of the project we will examine the graphical properties of even and odd functions.
In the process of completing this project you will be required to create a Word document containing answers to each question. Note that some portions of the exercise do not require any response in the final report. These sections should be completed in preparation for later questions in this lab. I do not expect anyone to attempt to learn the optional arguments for the plot commands used in this project. You should be able to copy and paste all necessary Maple commands from within this worksheet. If you have any questions, please ask Jay, Wally, or Prof. Meade.
Exercise 0
To define a function in Maple it suffices to specify the rule that maps a number in the domain to a number in the range. The domain is assumed to be the natural domain, i.e., the largest set of real numbers for which the function is defined. The general syntax is
f := x -> y
. Recall that
:=
is used to assign the value on its right-hand side to the name on its left-hand side. The
->
symbol creates a mapping from the object on its left to the object on its right. For example,
The next few lines show how this function can be evaluated and combined to form other expressions.
To plot a function, use the
plot
command (as introduced in Quiz 1):
a)
What Maple command defines the function
 ?
?
The next set of commands creates a table of values for the sine function
| > |
r := i*Pi/6; # angle, in radians
|
| > |
d := r*180/Pi; # angle, in degrees
|
| > |
y := f(r); # value of function
|
| > |
print( printf("%8a radians = %4a degrees, sin(%8a) = %a", r, d, r, y ) );
|
| > |
unassign( 'i', 'x', 'y' ): # technical detail to avoid problems later
|
The following commands produce plots of two shifts of the function
f
:
| > |
plot( f(x+a), x=-Pi..3*Pi );
|
| > |
plot( f(x)+a, x=-Pi..3*Pi );
|
Of course, a value for
a
must be specified and the domain can be changed as needed.
Sometimes it is more informative to include the original function in the graph. For example,
| > |
plot( [ f(x), f(x+a) ], x=-Pi..3*Pi );
|
| > |
plot( [ f(x), f(x)+a ], x=-Pi..3*Pi );
|
Notice that the only difference is that the first argument is now a list of functions. Maple automatically uses a different color for the different graphs in the plot.
The same approach could be used to create a plot with multiple shifts of the function. Before long, however, it becomes very tedious to type a long list of functions with regularly spaced values of the parameter. Maple's
repetition statement
(
for
...
do
...
end do
) can be used to automatically create a long list of functions.
| > |
fn_list := NULL: # initialize to empty
|
| > |
for a from -4 to 4 do # loop through values of a
|
| > |
fn_list := fn_list, f(x+a); # add next function
|
| > |
fn_list := [fn_list]; # convert to a list
|
| > |
plot( fn_list, x=-Pi..3*Pi );
|
b)
Read the online help for the repetition statement to learn how to obtain the list of functions f(x+a) for
 to
to
 in increments of 0.5. Include this plot (and only the plot) in your report.
in increments of 0.5. Include this plot (and only the plot) in your report.
There is a limit to the number of graphs that can reasonably be included in a single plot. In such situations animating the functions can be quite effective. There are several ways to create animations in Maple. One method is to create a list of plots and then to display them "in sequence". For example:
| > |
p_list := NULL: # initialize to empty
|
| > |
for a from -4 to 4 do # loop through values of a
|
| > |
p_list := p_list, plot( f(x+a), x=-Pi..3*Pi );
|
| > |
p_list := [p_list]: # convert to a list
|
The
display
command can be used to show the entire list of graphs in a single plot.
c)
Explain how the plot produced with the
display
command differs from the one obtained immediately before b)
To animate the list of plots, add
insequence=true
as an additional argument to the
display
command:
| > |
display( p_list, insequence=true );
|
This displays the first "frame" of the animation. Click on the graph. Notice the VCR-like (DVD-like?) control buttons that appear under the row of icons at the top of the Maple window. Click on the "Play" button to start the animation. Learn how to do each of the following:
-
step forward one frame at a time,
-
reverse the direction,
-
decrease the speed of the animation,
-
run the animation as a continuous loop.
For an example such as the one considered above, the
animate
command provides a much simpler way to obtain the same result
| > |
animate( f(x+a), x=-Pi..2*Pi, a=-4..4 );
|
What to do if the animate command does not work.
If the above command produces an error message stating
Error (in animate) Third argument must be a range in this case
the likely problem is that you assigned a value to the parameter earlier in the worksheet and did not unassign the name prior to using it in the
animate
command. To better understand what Maple is doing, execute the command
If
a
is assigned a value, this value is displayed. If
a
is not assigned a value, the unevaluated name is displayed. To remove the definition to the parameter by executing the following command:
d)
How many different frames are included in the animation created by the
display
command when the increment is 0.1?
How many different frames are included in the animation created by the
animate
command?
What additional argument must be added to the
animate
command to produce an animation with the same number of frames as the
display
command? (Hint: Read the online help for
animate
.)
Exercise 1
a) Horizontal shift:

Animate the graphs of
 for values of the parameter from
for values of the parameter from
 to
to
 in increments of 0.1.
in increments of 0.1.
b) Vertical shift:

Animate the graphs of
 for values of the parameter from
for values of the parameter from
 to
to
 in increments of 0.1.
in increments of 0.1.
c) Horizontal scaling:

Animate the graphs of
 for values of the parameter from
for values of the parameter from
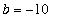 to
to
 in increments of 0.2.
in increments of 0.2.
d) Vertical scaling:

Animate the graphs of
 for values of the parameter from
for values of the parameter from
 to
to
 in increments of 0.2.
in increments of 0.2.
Exercise 2
Repeat all four (4) parts of Exercise 1 for the function
 .
.
Exercise 3
The graphs of the ten functions
f[1](x) = sin(2*x)+1
f[2](x) = -sin(x-1)
f[3](x) = 3*sin(2*x)
f[4](x) = 3*sin(x+1)
f[5](x) = 3*sin(2*x)+1
f[6](x) = -sin(x+1)
f[7](x) = 2*sin(x)+1
f[8](x) = 2*sin(x+1)
f[9](x) = 3*sin(2*x+1)
f[10](x) = 2*sin(2*x+1)
are shown in subsection i)-x) in a scrambled order.
i)
![[Maple Plot]](images/lab126.gif)
ii)
![[Maple Plot]](images/lab127.gif)
iii)
![[Maple Plot]](images/lab128.gif)
iv)
![[Maple Plot]](images/lab129.gif)
v)
![[Maple Plot]](images/lab130.gif)
vi)
![[Maple Plot]](images/lab131.gif)
vii)
![[Maple Plot]](images/lab132.gif)
viii)
![[Maple Plot]](images/lab133.gif)
ix)
![[Maple Plot]](images/lab134.gif)
x)
![[Maple Plot]](images/lab135.gif)
a)
Match each function with its graph. In addition, for each function, write a complete sentence describing how the function is related to the original function
 . (For example, "The graph of
. (For example, "The graph of
 is the graph of
is the graph of
 shifted one unit to the left and two units up.") Be sure your answer is neat and well-organized.
shifted one unit to the left and two units up.") Be sure your answer is neat and well-organized.
Exercise 4
To conclude this lab, we look at the graphical identification of even and odd functions. Recall that an even function is a function with the property that
 and an odd function satisfies
and an odd function satisfies
 . In both cases, we are interested in how the graph to the left of the
. In both cases, we are interested in how the graph to the left of the
 -axis (for
-axis (for
 <0) is related to the graph to the right of the
<0) is related to the graph to the right of the
 -axis (for
-axis (for
 >0). For an even function the graphs are mirror images and we say the graph is symmetric about the
>0). For an even function the graphs are mirror images and we say the graph is symmetric about the
 -axis. For an odd function the graph for
-axis. For an odd function the graph for
 <0 is the negative of the mirror image of the graph for
<0 is the negative of the mirror image of the graph for
 >0 and we say the graph is symmetric about the origin.
>0 and we say the graph is symmetric about the origin.
To determine if a given function, f, is even or odd (or neither), prepare a plot containing the graphs of
 (graphed as a black line),
(graphed as a black line),
 (graphed as red crosses), and
(graphed as red crosses), and
 (graphed as blue circles). If f is an even function then the red crosses are all on the black line, i.e.,
(graphed as blue circles). If f is an even function then the red crosses are all on the black line, i.e.,
 and f is an even function. If f is an odd function then the blue circles are all on the black line, i.e.,
and f is an even function. If f is an odd function then the blue circles are all on the black line, i.e.,
 . In all other situations, the function is neither even nor odd.
. In all other situations, the function is neither even nor odd.
To better understand these statements, consider the function
 on [
on [
 ,
,
 ].
].
| > |
f := x -> x^3 + sin(x);
|
The Maple command to produce the plot described above uses a few new optional arguments. Do not be concerned about the specifics of this command - except the first two argument (the list of functions to be graphed and the domain).
| > |
plot( [f(-x),f(x),-f(x)], x=-2*Pi..2*Pi, color=[black,red,blue], style=[line,point,point], symbol=[point,cross,circle], legend=["f(-x)","f(x)","-f(x)"] );
|
Hence, the function
 is an odd function.
is an odd function.
Use the graphical method described above to determine if each of the following functions is even, odd, or neither. (In your report, include a convincing plot on a reasonable domain.)
a)

b)

c)

d)

e)

f)

g)

h)

![]() , and the graphs of the related functions
, and the graphs of the related functions
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . In the second part of the project we will examine the graphical properties of even and odd functions.
. In the second part of the project we will examine the graphical properties of even and odd functions.
![[Maple Plot]](images/lab126.gif)
![[Maple Plot]](images/lab127.gif)
![[Maple Plot]](images/lab128.gif)
![[Maple Plot]](images/lab129.gif)
![[Maple Plot]](images/lab130.gif)
![[Maple Plot]](images/lab131.gif)
![[Maple Plot]](images/lab132.gif)
![[Maple Plot]](images/lab133.gif)
![[Maple Plot]](images/lab134.gif)
![[Maple Plot]](images/lab135.gif)





