Area and Riemann Sums
Calculus I Lab -- Fall 2002
prepared by
Douglas B. Meade
Department of Mathematics
University of South Carolina
Columbia, SC 29208
E-mail: meade@math.sc.edu
5 November 2002
Announcement
It is extremely unfortunate that the Election Day holiday coincided with the discussion of area. This might be THE topic that benefits most from the graphical and symbolic features of Maple. This worksheet contains an abreviated lab that is optional - but highly recommended. It is also designed to be very simple to complete. You should be able to complete all work for this lab in well under an hour.
Prepare your lab report as a handwritten summary, a Word document, or a Maple worksheet. Regardless of the format used to prepare your report, your answers MUST appear as complete English sentences. Simply stating the "answer" is not acceptable. This lab is due no later than 5:00p.m. Friday, November 8, 2002. It can be handed to either Wally or Prof. Meade or e-mailed to
waltman@sc.edu
.
Purpose
The purpose of this week's lab is to provide a coordinated visual and symbolic look at area and Riemann sums. The
RiemannSum
command from the
Student[Calculus1]
package will be used to create graphical and symbolic approximations to the area under a curve
 over an interval [
over an interval [
 ,
,
 ]. The commands introduced in this worksheet can be used to check your work for many of the assigned problems from Sections 5.4 (p. 233) and 5.5 (p. 240).
]. The commands introduced in this worksheet can be used to check your work for many of the assigned problems from Sections 5.4 (p. 233) and 5.5 (p. 240).
Example: Area by Inscribed Polygons
| > |
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Consider the region R bounded by the parabola
 =
=
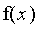 =
=
 , the
, the
 -axis, and the veritcal line
-axis, and the veritcal line
 .
.
| > |
plot( y, x=0..2, filled=true, scaling=constrained );
|
![[Maple Plot]](images/lab109.gif)
We refer to R as the region under the curve
 between
between
 and
and
 . Our main aim is to calculate the area of R,
. Our main aim is to calculate the area of R,
 .
.
Partition the interval [ 0, 2 ] into
 (equal) subintervals, each with length
(equal) subintervals, each with length
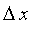 = (2-0)/
= (2-0)/
 , by means of the
, by means of the
 points
points
0 =
![x[0]](images/lab1018.gif) <
<
![x[1]](images/lab1019.gif) <
<
![x[2]](images/lab1020.gif) < ... <
< ... <
![x[n-1]](images/lab1021.gif) <
<
![x[n]](images/lab1022.gif) = 2
= 2
where
![x[0]](images/lab1023.gif) = 0,
= 0,
![x[1]](images/lab1024.gif) =
=
 =
=
 ,
,
![x[2]](images/lab1027.gif) =
=
 =
=
 , ...,
, ...,
![x[i]](images/lab1030.gif) =
=
 =
=
 , ..., and
, ..., and
![x[n]](images/lab1033.gif) =
=
 = 2.
= 2.
Consider the typical rectangle with base [
![x[i-1]](images/lab1035.gif) ,
,
![x[i]](images/lab1036.gif) ] and height
] and height
![f(x[i-1]) = x[i-1]^2](images/lab1037.gif) ; its area is
; its area is
![f(x[i-1])*Delta*x](images/lab1038.gif) . For example, the union
. For example, the union
![R[7]](images/lab1039.gif) of all 7 rectangles forms the inscribed polygon shown below
of all 7 rectangles forms the inscribed polygon shown below
| > |
RiemannSum( y, x=0..2, partition=7, method=lower, output=plot,
showarea=false, scaling=constrained,
title="Area under y=x^2, 0<x<2, with 7 inscribed rectangles" );
|
![[Maple Plot]](images/lab1040.gif)
The area
![A(R[7])](images/lab1041.gif) can be calculated by summing the areas of the 7 rectangles:
can be calculated by summing the areas of the 7 rectangles:
| > |
A_R7 := RiemannSum( y, x=0..2, partition=7, method=left, output=sum );
|

The value of this sum,
| > |
value( A_R7 ) = evalf( A_R7 );
|

is an approximation to the area of R.
The area
![A(R[n])](images/lab1044.gif) can be calculated by summing the areas of the
can be calculated by summing the areas of the
 rectangles in
rectangles in
![R[n]](images/lab1046.gif) :
:
| > |
A_Rn := RiemannSum( y, x=0..2, partition=n, method=left, output=sum );
|

The value of this sum is
| > |
q1 := value( A_Rn ):
q2 := expand( q1 ):
q1 = q2;
|

Note that Maple has applied the formula for the sum of squares of integers to obtain this result.
The following animation will help you to visualize what happens as
 gets larger and larger.
gets larger and larger.
| > |
p1 := RiemannSum( y, x=0..2, partition=7, iterations=6, method=lower, output=animation,
scaling=constrained ):
|
![[Maple Plot]](images/lab1050.gif)
For the purposes of a printed handout, the following command displays the individual frames of the animation.
![[Maple Plot]](images/lab1051.gif)
Observe that the approximating area appear to be converging to a value slightly larger than 2.6.
The exact value of A(R) is the limit of the approximating areas as n increases without bound:
| > |
q3 := Limit( q2, n=infinity ):
q3 = value( q3 );
`` = evalf( value(q3) );
|


Example: Area by Circumscribed Polygons
The careful reader will notice that while the inscribed polygons appear to fill the entire region R, the preceding argument only provides a lower bound on the area of R:
![Limit(A(R[n]),n = infinity)](images/lab1054.gif) <= A( R ) .
<= A( R ) .
Consider now the union
![S[n]](images/lab1055.gif) of the
of the
 rectangles formed with base [
rectangles formed with base [
![x[i-1]](images/lab1057.gif) ,
,
![x[i]](images/lab1058.gif) ] and height
] and height
![f(x[i]) = x[i]^2](images/lab1059.gif) . For example, with
. For example, with
 :
:
| > |
RiemannSum( y, x=0..2, partition=7, method=upper, output=plot,
showarea=false, scaling=constrained,
title="Area under y=x^2, 0<x<2, with 7 circumscribed rectangles" );
|
![[Maple Plot]](images/lab1061.gif)
The area
![A(S[7])](images/lab1062.gif) can be calculated by summing the areas of the 7 rectangles:
can be calculated by summing the areas of the 7 rectangles:
| > |
A_S7 := RiemannSum( y, x=0..2, partition=7, method=right, output=sum );
|

The value of this sum,
| > |
value( A_S7 ) = evalf( A_S7 );
|

is an (over) approximation to the area of R.
The area
![A(S[n])](images/lab1065.gif) can be calculated by summing the areas of the
can be calculated by summing the areas of the
 rectangles in
rectangles in
![S[n]](images/lab1067.gif) :
:
| > |
A_Sn := RiemannSum( y, x=0..2, partition=n, method=right, output=sum );
|

The value of this sum is
| > |
q4 := value( A_Sn ):
q5 := expand( q4 ):
q4 = q5;
|
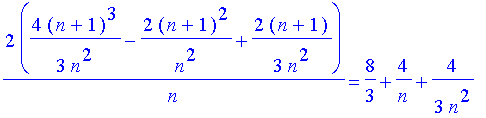
The following animation will help you to visualize what happens as
 gets larger and larger.
gets larger and larger.
| > |
p2 := RiemannSum( y, x=0..2, partition=7, iterations=6, method=upper, output=animation,
scaling=constrained ):
|
![[Maple Plot]](images/lab1071.gif)
For the purposes of a printed handout, the following command displays the individual frames of the animation.
| > |
plots[display]( op([1],p2) );
|
![[Maple Plot]](images/lab1072.gif)
Once again, observe that the approximating area appear to be converging to a value slightly larger than 2.6. In fact, as before,
| > |
q6 := Limit( q5, n=infinity ):
q6 = value( q6 );
|

In conclusion, because each
![A(R[n])](images/lab1074.gif) is an under approximation to
is an under approximation to
 and each
and each
![A(S[n])](images/lab1076.gif) is an over approximation to
is an over approximation to
 :
:
![Limit(A(R[n]),n = infinity)](images/lab1078.gif) <=
<=
 <=
<=
![Limit(A(S[n]),n = infinity)](images/lab1080.gif)
And, by the Squeeze Theorem for Limits and the fact that each of these limits has the same value, we conclude that
 .
.
Exercise 1
Consider the region R under the curve
 over the interval [ 1, 9 ]. Let
over the interval [ 1, 9 ]. Let
![R[n]](images/lab1083.gif) and
and
![S[n]](images/lab1084.gif) denote the unions of rectangles formed with polygons formed using the value of the function at the left and right endpoints of each subinterval. (Note that because the curve is not monotone on this interval, these are
NOT
inscribing and circumscribing polygons.)
denote the unions of rectangles formed with polygons formed using the value of the function at the left and right endpoints of each subinterval. (Note that because the curve is not monotone on this interval, these are
NOT
inscribing and circumscribing polygons.)
(a) Use the
RiemannSum
command (with
method=left
) to obtain the expression for
![A(R[n])](images/lab1085.gif) as the sum of a constant and two negative powers of
as the sum of a constant and two negative powers of
 .
.
(b) Use the
RiemannSum
command (with
method=right
) to obtain the expression for
![A(S[n])](images/lab1087.gif) as the sum of a constant and two negative powers of
as the sum of a constant and two negative powers of
 .
.
(c) What is
 ?
?
(d) Bonus Question: What is the smallest number of partitions (with
method=left
) needed to approximate the value of
 to one decimal place, i.e., with an error no more than 0.05. (Explain how you know your answer is correct.)
to one decimal place, i.e., with an error no more than 0.05. (Explain how you know your answer is correct.)
Exercise 2 (# 19, page 234)
In the notation of this problem,
![A[a]^b](images/lab1091.gif) is the area under the curve
is the area under the curve
 over the interval [
over the interval [
 ,
,
 ]. For parts (a) and (b) in the text, follow the following steps:
]. For parts (a) and (b) in the text, follow the following steps:
(i) Use the
RiemannSum
command to obtain an approximation to
![A[a]^b](images/lab1095.gif) with
with
 subintervals when the approximating rectangles are formed at the left end of each subinterval.
subintervals when the approximating rectangles are formed at the left end of each subinterval.
(ii) Explain how you get from this expression to the exact value for
![A[0]^b](images/lab1097.gif) and
and
![A[a]^b](images/lab1098.gif) .
.
![]() over an interval [
over an interval [
![]() ,
,
![]() ]. The commands introduced in this worksheet can be used to check your work for many of the assigned problems from Sections 5.4 (p. 233) and 5.5 (p. 240).
]. The commands introduced in this worksheet can be used to check your work for many of the assigned problems from Sections 5.4 (p. 233) and 5.5 (p. 240).
![[Maple Plot]](images/lab109.gif)
 between
between
![[Maple Plot]](images/lab1040.gif)




![[Maple Plot]](images/lab1050.gif)
![[Maple Plot]](images/lab1051.gif)

![Limit(A(R[n]),n = infinity)](images/lab1054.gif) <= A( R ) .
<= A( R ) .
![[Maple Plot]](images/lab1061.gif)



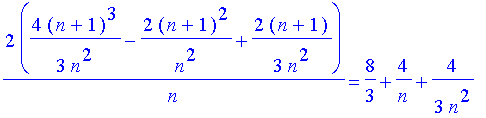
![[Maple Plot]](images/lab1071.gif)
![[Maple Plot]](images/lab1072.gif)

![Limit(A(R[n]),n = infinity)](images/lab1078.gif) <=
<=
![Limit(A(S[n]),n = infinity)](images/lab1080.gif)
 .
.
 over the interval [ 1, 9 ]. Let
over the interval [ 1, 9 ]. Let
 over the interval [
over the interval [