Systemwide Workshop for Calculus and Maple at USC
Introduction to Maple 8
Douglas B. Meade
E-mail:
meade@math.sc.edu
WWW URL:
http://www.math.sc.edu/~meade/
Objectives
-
Working with the Maple GUI
-
Entering mathematical expressions
-
Plotting functions and points
-
The fundamentals for algebra and calculus
-
Maplets
What is Maple?
Much of your mathematical background has probably been focused on developing the ability to solve equations and explore functions. The sophisticated manipulation of symbols and expressions that you use to solve equations and investigate functions can also be performed by software packages called computer algebra systems (CAS). A CAS can be use to generate the exact symbolic solutions you obtained by hand, the numerical approximations you found using a calculator, and the graphs you have drawn. Maple is one of several CAS's; other major examples are Mathematica, Macsyma, Derive, and MathCad.
Maple is a product of
Maplesoft (formerly Waterloo Maple). Other products in the Maple suite are
MapleNet and
MapleTA.
Maple can be used in many different ways. In a course where students are developing manual manipulative skills, the primary uses of Maple are likely to be the graphical display of functions and the use of custom-built
maplets
illustrating a specific concept from the course. In later courses Maple's symbolic manipulation features can be utilized by students to emphasize higher-level concepts by letting the software assist with the manipulations. As students become familiar with Maple they should see that it will be of use in a wide variety of courses.
Getting Started with the Maple GUI
Documentation and Online Help
The on-line help for Maple is very good. The help pages describe the syntax of each command, a brief description of the algorithm that has been implemented, and a few examples illustrating the use of the command. To obtain help on the command func , type:
?func
in any input region. The
Help
dropdown menu on the menu bar provides a number of different ways to access Maple's help system.
Topic Search
and
Full Text Search
are two interactive interfaces to the entire Maple help system.
To get started, select the
Glossary
entry and take a few minutes to become familiar with some of the terminology related to Maple and its graphical user interface.
If you have more time and are a new Maple user take the
New User's Tour
; if you have used earlier versions of Maple, select the
What's New
entry.
A final suggestion is that anytime you want to see the Maple help for a command or other word in a Maple worksheet, position the cursor anywhere in that word and press
Ctrl-F1
. This is Maple's context-sensitive help.
Worksheets
The worksheet is the basic Maple document. (Use Maple's context-sensitve help to view the online help for worksheets.)
You have already learned how to open up a worksheet. After Maple is opened, position the cursor arrow on the menu item
File
and click the left button once. You can select
New
to obtain a fresh, empty worksheet. Or you can select
Open
to choose an existing worksheet (the name will always end with
.mws
), either by double clicking on the name or by selecting the name and then pressing the Open button.
Once in a worksheet the current location is marked by the cursor, a vertical bar. You can move around by moving the mouse and then clicking the left button once, by using the arrow keys, or by using the scroll bar up and down arrows on the right side of this window followed by finer adjustment with the mouse. An input region (marked by the > prompt with words in bright red) is executed by positioning the cursor anywhere on the desired line and pressing the
Enter
key. In summary: use the mouse to position yourself within a Maple worksheet, and the
Enter
key to instruct Maple to actually do something.
It is probably a good idea to begin EVERY worksheet that you create with the following commands.
Warning, the name changecoords has been redefined
| > |
with( Student[Calculus1] );
|
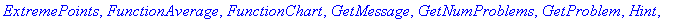
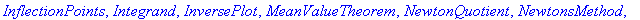
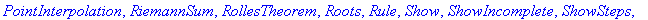
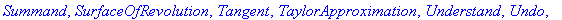
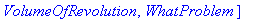
Maple's output is shown in blue immediately following the execution group containing the command(s). The context menus provide one way to perform additional operations. To use a context menu, select the output, or portion of output, and click the right mouse button. After a few seconds a menu will appear; the entries in this menu are operations that are most common for an object of this type. (Try this on some of the output later in this worksheet.)
Remember to save your work periodically. If you forget to save your work and the computer crashes you will lose any work done since the last time you saved the worksheet.
Essential Maple Facts
Maple is a computer language; it cannot read your mind. You need to learn how to communicate with Maple. The Maple 8 Quick Reference Guide is available as a PDF file on the WWW at
http://www.math.sc.edu/~meade/maple/maple-ref.pdf.
A few of the essentials are:
-
assignments are made with
:=
(plain
=
has a different meaning)
think of this as giving the value of the right hand side to the name that appears on the left hand side
-
every command is terminated by a semi-colon (
;
) or colon (
:
)
with the latter the computation is done, but the result is not displayed
-
the percent sign (
%
) refers to the result of the immediately preceding computation
-
Maple is case sensitive -- that is, the names
x
and
X
are different,
pi
,
Pi
, and
PI
are all different
-
{ }
-- set notation (mostly used in specifying a system of equations or a set of unknown variables))
-
a .. b
-- this is how Maple indicates the interval [
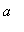 ,
,
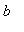 ] , that is, the real numbers from
] , that is, the real numbers from
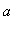 to
to
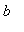
-
?
or
help
-- a request to Maple for information from the online help archive
The standard mathematical functions are denoted by their standard symbols and names:
+
(plus) ,
-
(minus) ,
*
(times) ,
/
(divided by) ,
^
(raised to the power) ,
sin
,
cos
,
tan
,
abs
,
sqrt
, ...
In the following lines, use paper and pencil to first predict what you think Maple will do. Then execute the command and see what actually happens!
| > |
number:= 4 * 6 + 12 / 6 - 1 ;
|
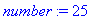
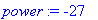
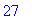
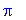
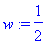
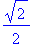
Error, (in tan) numeric exception: division by zero
| > |
3 / ( 5 - sqrt( number ) ) ;
|
Error, numeric exception: division by zero
Now enter some commands of your own! To produce the input prompt ( > ) use the
[>
button in the Menu Bar. Be generous with the space bar to make your commands easy to read, and to edit (modify after the fact). Go back to the tangent calculation above (remember how to reposition the cursor!) and change it to compute the tangent of
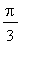 . Find how Maple represents
. Find how Maple represents
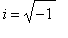 . Use Maple to find the real and imaginary parts of
. Use Maple to find the real and imaginary parts of
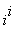 .
.
Next we define some functions for later use. Notice how Maple uses the current value for any name that appears on the right-hand side of an assignment.
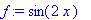
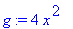
| > |
h := 0.25 * cos( 8*x ) ;
|
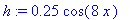
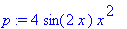
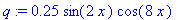
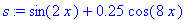
Plotting
Graphs of functions are produced by the plot command. In its simplest form, plot needs to know the function to be plotted and the range of values for the independent variable. Note that
a..b
is Maple's way of describing the interval [
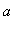 ,
,
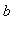 ]. Observe that some of the graphs have personalized titles. When you actually print plots to turn in to be graded, they MUST have a title and signature [by your initials or last name]. Again, try to predict the output before tapping the
Enter
key!
]. Observe that some of the graphs have personalized titles. When you actually print plots to turn in to be graded, they MUST have a title and signature [by your initials or last name]. Again, try to predict the output before tapping the
Enter
key!
| > |
plot( 3 * t - 2 , t = -3 .. 10 ) ; # WAIT FOR THE GRAPH TO APPEAR!!
|
![[Maple Plot]](images/USCworkshop35.gif)
| > |
plot( f , x = -Pi .. 2 * Pi ) ;
|
![[Maple Plot]](images/USCworkshop36.gif)
| > |
plot( p , x = -6 .. 8 , title = ` f * g [by DM] ` );
|
![[Maple Plot]](images/USCworkshop37.gif)
These plots are nice, but what information do they convey? Let's concentrate on the plot of
p
, that is
f*g
. Position the cursor on a point on the graph and click the left mouse button. The numbers that appear on the upper-left corner are the coordinates of the current location of the cursor. Use this technique to estimate the global maximum and minimum values of
f*g
on the interval [-6, 8], and the
 -values at which these are found. Where do other (local) minima and maxima occur? Can you guess the exact values?
-values at which these are found. Where do other (local) minima and maxima occur? Can you guess the exact values?
| > |
plot(2 * u^3 + 4 * u - 5 , u = -10 .. 7 , title = ` cubic function [by DM] ` ) ;
|
![[Maple Plot]](images/USCworkshop39.gif)
Where does the cubic function cross the
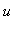 -axis? Maybe it would be helpful to cut down the plotting interval from [-10, 7] to [-1, 3], or even narrower, say to [0, 1.5]. Try it. Can you find the
-axis? Maybe it would be helpful to cut down the plotting interval from [-10, 7] to [-1, 3], or even narrower, say to [0, 1.5]. Try it. Can you find the
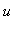 -intercept to 2-decimal point accuracy by this process? It is a powerful method, which we call ZOOMING IN. (You will be expected to remember this and use this regularly at various times throughout this course.)
-intercept to 2-decimal point accuracy by this process? It is a powerful method, which we call ZOOMING IN. (You will be expected to remember this and use this regularly at various times throughout this course.)
| > |
plot( s , x = 0 .. 3 * Pi );
|
![[Maple Plot]](images/USCworkshop42.gif)
| > |
plot( q , x = -1.2 .. 1.2 ) ;
|
![[Maple Plot]](images/USCworkshop43.gif)
Can you explain why the graphs of
s
and
q
look the way they do? One way to answer this question is to include the graphs of f and h along with the plot of s.
| > |
plot( [ s, f, h ], x=0..3*Pi );
|
![[Maple Plot]](images/USCworkshop44.gif)
Maple's choice of colors is not optimal. Alternate colors can be specified as an optional argument to the
plot
command:
| > |
plot( [ s, f, h ], x=0..3*Pi, color=[red,cyan,pink] );
|
![[Maple Plot]](images/USCworkshop45.gif)
Some features of the plot can be controlled interactively. Click the left mouse button anywhere in a graph. A frame should appear around the plot; the plot can be resized by dragging the control points. The context menu for a plot contains entries for tweaking the plot. Use the context menu to add a legend to the plot, then customize the legend labels to make a more informative picture. (Legends can be added directly at the command line as well, see
?plot,options
.)
| > |
plot( [ s, f, h ], x=0..3*Pi,
color=[red,cyan,pink],
legend=[ "s=f+h","f","h"] );
|
![[Maple Plot]](images/USCworkshop46.gif)
This only touches the surface (pun intended!) of Maple's graphical capabilities. Maple is able to produce high-quality renderings of 3D surfaces with real-time rotation, 2D and 3D animations, vector fields, solutions of differential equations, ....
Algebra
Consider the rational function
| > |
F := (t^2+3*t+2)^3/(t+1)^4;
|
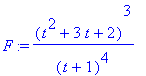
There are a number of commands that could be used to ``simplify'' this function:
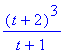
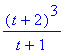
If you want to extract parts of the expression:
| > |
Fnum := numer( F );
Fden := denom( F );
|
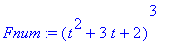
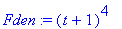
| > |
expand( Fnum );
expand( Fden );
|
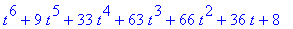
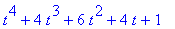
and recombine them to form an equivalent expression
| > |
F2 := expand( Fnum ) / expand( Fden );
|
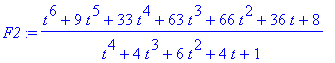
| > |
F3 := factor( Fnum ) / factor( Fden );
|
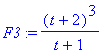
Note that Maple automatically simplifies results prior to displaying the result.
Compare the results of the following
solve
commands:
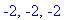
| > |
solve( numer(F)=0, t );
|
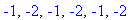
| > |
solve( numer(F)=0, {t} );
|
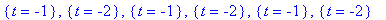
| > |
{ solve( numer(F)=0, t ) };
|
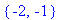
| > |
[ solve( numer(F)=0, t ) ];
|
![[-1, -2, -1, -2, -1, -2]](images/USCworkshop60.gif)
The syntax to solve a system of equations is illustrated with
| > |
sys := { x^2 + y^2 = 6,
2*x + y = 4 }:
|
| > |
sol1 := solve( sys, var );
|
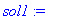
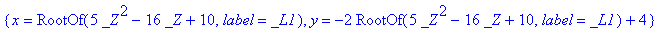
| > |
sol2 := allvalues( sol1 );
|
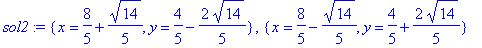
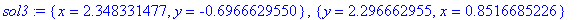
| > |
sol4 := fsolve( sys, var );
|
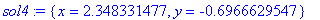
Calculus
Limits
Maple supports both two-sided and one-sided limits. In the first examples, the inert command
Limit
and
value
are used to create a nicer visual presentation
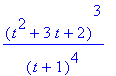
| > |
L1 := Limit( F, t=1 ):
L1 = value( L1 );
|
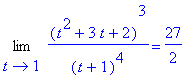
| > |
Lm1 := Limit( F, t=-1 ):
Lm1 = value( Lm1 );
|
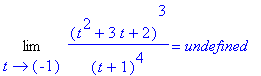
| > |
limit( F, t=-1, left ) <> limit( F, t=-1, right );
|

Derivatives
Derivatives are computed with Maple's
diff
command. There is an inert differentiation command,
Diff
, that can be used as shown above with
Limit
.)
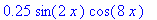
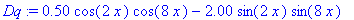
| > |
SP := solve( Dq=0, x );
|
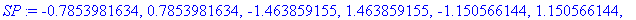
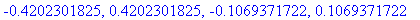
Compare the above results with the same operations applied to the same function - except that the coefficient is a rational number.
| > |
q2 := convert( q, rational );
|
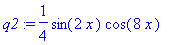
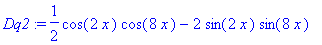
| > |
SP2 := solve( Dq2, x );
|

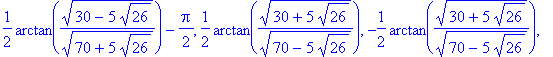
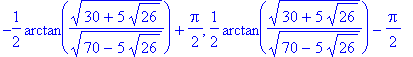
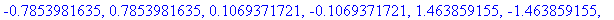
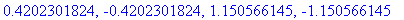
In general, Maple returns floating point results only when explicitly requested by the user or when the input arguments include floating point numbers.
Integrals
Definite and indefinite integrals are handled with the
int
(and
Int
) commands.
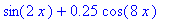
| > |
S := Int( s, x ); # Notice there is no constant of integration!
|
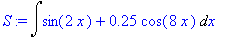
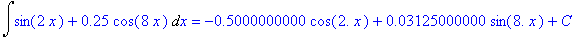
And, now for definite integrals with floating-point and rational coefficients:
| > |
S2 := int( s, x=0..2*Pi/3 );
|
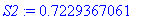
| > |
s2a := convert( s, rational );
|
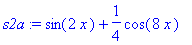
| > |
S2a := int( s2a, x=0..2*Pi/3 );
|
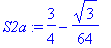
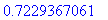
Note that these values are obtained via the Fundamental Theorem of Calculus.
Maple can do
numerical integration
(but does not use the methods generally taught in Calculus). For this problem a numerically computed approximation to the definite integral could be obtained with the use of
evalf
and
Int
:
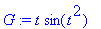
![[Maple Plot]](images/USCworkshop89.gif)
| > |
q1 := Int( G, t=0..10 );
|
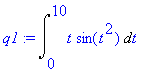
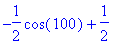
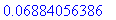
For educational purposes, the
ApproximateInt
command in the
Student[Calculus1]
package knows about all of the methods taught in Calculus. The
ApproximateIntegration
maplet [
Maplet Viewer][
MapleNet] is a built around this command.
Maplets
This topic requires more time and space than is available in this session. I offered a 2-hour workshop in Maplets at ICTCM XV last November. The
worksheet, and
all other files, for that workshop can be downloaded from the WWW.
If you are not interested in maplet programming, you should still take a look at some of the maplets that are available for use with Calculus. The
interactive
command in the
plots
package is one of the most involved maplets.
| > |
interactive( x*y*sin(x+y) );
|
![[Maple Plot]](images/USCworkshop93.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
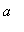 ,
,
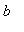 ] , that is, the real numbers from
] , that is, the real numbers from
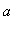 to
to
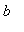
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Find how Maple represents
. Find how Maple represents
![]() . Use Maple to find the real and imaginary parts of
. Use Maple to find the real and imaginary parts of
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/USCworkshop35.gif)
![[Maple Plot]](images/USCworkshop36.gif)
![[Maple Plot]](images/USCworkshop37.gif)
![[Maple Plot]](images/USCworkshop39.gif)
![[Maple Plot]](images/USCworkshop42.gif)
![[Maple Plot]](images/USCworkshop43.gif)
![[Maple Plot]](images/USCworkshop44.gif)
![[Maple Plot]](images/USCworkshop45.gif)
![[Maple Plot]](images/USCworkshop46.gif)
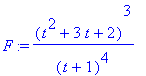
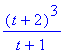
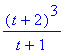
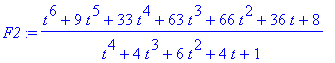
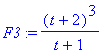
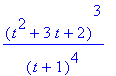
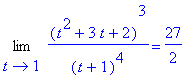
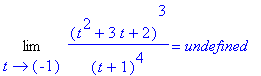

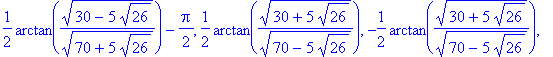
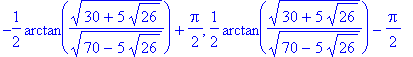
![[Maple Plot]](images/USCworkshop89.gif)
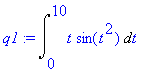
![[Maple Plot]](images/USCworkshop93.gif)