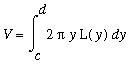Volume.mws
Volume of a Solid
| > |
restart;
with( plots ):
with( Student[Calculus1] ):
|
Warning, the name changecoords has been redefined
Lesson Overview
If a solid can be sliced into infinitely thin cross-sections with known area, then the volume of the solid can be written as a definite integral with the cross-sectional area as the integrand. The cross-sections can be horizontal or vertical. The general form for the definite integral of a solid with cross-sections with area
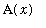 for
for
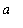 <=
<=
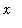 <=
<=
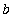 is
is
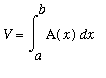 .
.
The
Method of Disks
(or
Washers
). The general form of the definite integral for the Method of Disks with slices cut perpendicular to the
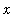 -axis is
-axis is
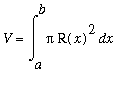 .
.
This is just the method for a solid with known cross-section in which the cross-sections are circles with radius
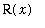 for
for
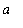 <=
<=
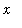 <=
<=
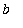 .
.
Another way to compute volumes with definite integrals is the
Method of Shells
. The general idea for shells is to view the solid as a collection of infinitely thin concentric shells. Here the defnite integral has limits of integration corresponding to the smallest and largest radius of a shell and the integrand is the surface area of the shell. The general form for a definite integral for the Method of Shells with shells centered on the
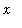 -axis is
-axis is
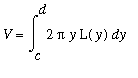 .
.
where
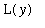 is the length of the shell with radius
is the length of the shell with radius
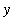 for all radii
for all radii
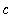 <=
<=
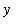 <=
<=
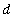 .
.
The
Volume of Revolution
maplet [
Maplet Viewer][
MapleNet] should be used to visualize solids formed by revolving a curve around either the
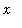 - or
- or
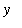 -axis.
-axis.
Maplet Requests:
Washers
and
Shells
It would be nice to have Washer and Shells maplets. These maplets would be similar to the Area maplet. The fundamental difference would be that the plot is 3D and the slices are either 2D cross sections (Washer) or 3D shells (Shells). The real key is to be able to see not only the region but also the slices..
Maplet Request:
Volume of Revolution
This maplet could be a good start to the Washers maplet, but I think the purposes are sufficiently distinct to warrant separate maplets. I would like to see this maplet modified to allow axes other than the coordinate axes.
Example 1: Method of Disks
Find the volume of the solid of revolution formed by revolving the graph of y=sqrt(x) on [ 0, 1 ] about the x-axis.
To begin, use the
Volume of Revolution
maplet [
Maplet Viewer][
MapleNet] to visualize this solid. Within the maplet window, change the
Function
to
sqrt(x)
with
a =
0
and
b =
1
; then click the
Plot
button. A three-dimensional plot of the solid will appear in the plot region of the maplet GUI. Alternatively, the solid can be constructed as follows:
| > |
top := sqrt(x):
VolumeOfRevolution( top, x=0..1, output=plot, style=patchnogrid );
|
![[Maple Plot]](images/Volume21.gif)
The volume of this solid can be computed by the Method of Disks because the cross-sections perpendicular to the x-axis are circular disks. The slice at x has radius sqrt(x) and cross-sectional area Pi*(sqrt(x))^2 = Pi*x. Thus,
| > |
R_disk := top:
A_disk := Pi * top^2:
R[disk] = R_disk;
A[disk] = A_disk;
|
![R[disk] = x^(1/2)](images/Volume22.gif)
![A[disk] = Pi*x](images/Volume23.gif)
and the volume is given by the definite integral
| > |
V1 := Int( A_disk, x=0..1 ):
V[`solid 1`] = V1;
`` = value( V1 );
|
![V[`solid 1`] = Int(Pi*x,x = 0 .. 1)](images/Volume24.gif)
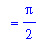
The definite integral and its value can be obtained in the
Volume of Revolution
maplet [
Maplet Viewer][
MapleNet] by clicking on the
Volume
button. Or, within the Maple worksheet interface,
| > |
V1a := VolumeOfRevolution( top, x=0..1, output=integral ):
V1a = value( V1a );
`` = evalf( value(V1a) );
|
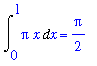

Example 2: Method of Washers
Find the volume of the solid of revolution formed by revolving the region bounded by the graphs of
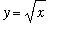 ,
,
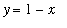 , and
, and
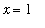 about the
about the
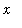 -axis.
-axis.
The region to be revolved about the
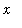 -axis can be determined by first plotting the graphs of
-axis can be determined by first plotting the graphs of
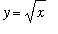 and
and
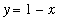 on the interval [ 0, 1 ].
on the interval [ 0, 1 ].
| > |
bot := 1-x:
P1 := plot( [top,bot], x=0..1, color=[red,blue] ):
P1;
|
![[Maple Plot]](images/Volume35.gif)
The two graphs intersect at
| > |
left := solve( top=bot ):
x = left;
|
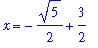
This is the left endpoint of the interval of integration; the right endpoint will be
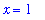
The region to be revolved around the x-axis is outlined in yellow in the following plot
| > |
P2 := plot( [top,bot], x=left..right, color=yellow, thickness=5 ):
P3 := plot( [[1,0],[1,1]], style=line, color=yellow, thickness=5 ):
display( P1,P2,P3 );
|
![[Maple Plot]](images/Volume38.gif)
The solid of revolution can be displayed with a single use of the
VolumeOfRevolution
command:
| > |
VolumeOfRevolution( top,bot, x=left..right, output=plot, view=[0..1,DEFAULT,DEFAULT], style=patchnogrid );
|
![[Maple Plot]](images/Volume39.gif)
For each
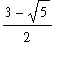 <
<
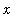 < 1, the cross-section at
< 1, the cross-section at
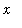 perpendicular to the
perpendicular to the
 -axis is a circular washer with outer radius
-axis is a circular washer with outer radius
| > |
Rout := top:
R[outer] = Rout;
|
![R[outer] = x^(1/2)](images/Volume44.gif)
and inner radius
| > |
Rin := bot:
R[inner] = Rin;
|
![R[inner] = 1-x](images/Volume45.gif)
The area of this washer is
| > |
Awasher := Pi*Rout^2 - Pi*Rin^2:
A[washwer] = Awasher;
`` = factor( Awasher );
|
![A[washwer] = Pi*x-Pi*(1-x)^2](images/Volume46.gif)
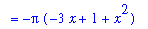
The volume of this solid is given by the definite integral
| > |
V2 := Int( Awasher, x=left..right ):
V[`solid 2`] = V2;
`` = simplify(value( V2 ));
`` = evalf( value( V2 ) );
|
![V[`solid 2`] = Int(Pi*x-Pi*(1-x)^2,x = -1/2*5^(1/2)+3/2 .. 1)](images/Volume48.gif)
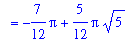
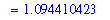
N ote that the
VolumeOfRevolution
maplet does not (yet) support the Method of Washers.
Example 3: Method of Shells
The volume of the solid of revolution formed by revolving about the
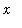 -axis the region bounded by the graphs of
-axis the region bounded by the graphs of
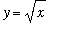 ,
,
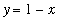 , and
, and
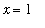 can be represented as the sum of two definite integrals from the Method of Washers, or a single definite integral from the Method of Shells.
can be represented as the sum of two definite integrals from the Method of Washers, or a single definite integral from the Method of Shells.
The region in the
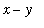 plane that is to be revolved about the
plane that is to be revolved about the
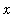 -axis is outlined in cyan in the plot below:
-axis is outlined in cyan in the plot below:
| > |
Left := bot:
Right := top:
Top := 1:
Bot := eval( Left, x=left ):
|
| > |
P4 := plot( [Top,Left], x=0..left, color=cyan, thickness=5 ):
P5 := plot( [Top,Right], x=left..1, color=cyan, thickness=5 ):
display( P1,P4,P5 );
|
![[Maple Plot]](images/Volume57.gif)
The solid of revolution is rendered in the following plot. [Rotate the plot to see through the whole and to see other features of this solid.]
| > |
VolumeOfRevolution( 1,piecewise(x<left,Left,Right), x=0..1, output=plot, style=hidden );
|
![[Maple Plot]](images/Volume58.gif)
Using the Method of Washers, the volume of the solid of revolution can be written as the sum of two separate definite integrals
| > |
V3washer := VolumeOfRevolution( Top,Left, x=0..left, output=integral )
+ VolumeOfRevolution( Top,Right, x=left..1, output=integral ):
V[washer] = V3washer;
`` = simplify( value( V3washer ) );
`` = evalf( value( V3washer ) );
|
![V[washer] = Int((2-x)*Pi*x,x = 0 .. -1/2*5^(1/2)+3/2)+Int(Pi*(1-x),x = -1/2*5^(1/2)+3/2 .. 1)](images/Volume59.gif)
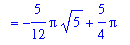
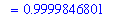
By the Method of Shells, there are shells for every y with (sqrt(5)-1)/2 < y < 1. The radius of each shell is y. The height (length) of each shell is the horizontal distance between points on the graphs of y=1-x and y=sqrt(x) for this value of y. That is, writing these two curves as functions of y: x=1-y and x=y^2, the height of the shell is y^2 - (1-y).
| > |
Lefty := 1-y:
Righty := y^2:
R[shell] := y;
L[shell] := Righty - Lefty;
|
![R[shell] := y](images/Volume62.gif)
![L[shell] := y^2-1+y](images/Volume63.gif)
Thus, the definite integral for the volume of this solid by the Method of Shells is
| > |
V3shell := Int( 2*Pi*R[shell]*L[shell], y=Bot..Top ):
V[shell] = V3shell;
`` = simplify( value( V3shell ) );
`` = evalf( value( V3shell ) );
|
![V[shell] = Int(2*Pi*y*(y^2-1+y),y = -1/2+1/2*5^(1/2) .. 1)](images/Volume64.gif)
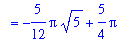
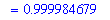
Observe that the two integrals have the same value and that this value is not 1.
Example 4: Method for Solid with Known Cross Section
The Methods of Disks and Washers are special cases of the Method for a Solid with Known Cross Section. To illustrate the generality of the Method for Solids with Known Cross Section, consider the solid constructed above the region bounded by the graphs of
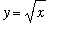 ,
,
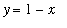 , and the
, and the
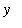 -axis (shown below, highlighted in turquoise) assuming each cross-sectional slice perpendicular to the
-axis (shown below, highlighted in turquoise) assuming each cross-sectional slice perpendicular to the
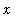 -axis is an equilateral triangle.
-axis is an equilateral triangle.
| > |
P6 := plot( [top,bot], x=0..left, color=turquoise, thickness=5 ):
P7 := plot( [[0,0],[0,1]], color=turquoise, thickness=5 ):
display( P1,P6,P7 );
|
![[Maple Plot]](images/Volume71.gif)
The upper surface of this region can be constructed using the fact that the base of each equilateral triangle has base
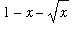 and height
and height
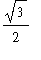 (base). The surface with these properties is shown below.
(base). The surface with these properties is shown below.
| > |
F1 := sqrt(3)*(y-top):
F2 := sqrt(3)*(bot-y):
F := piecewise( y<=(bot+top)/2, F1, y>(bot+top)/2, F2 );
plot3d( F, y=bot..top, x=0..left, view=[0..1,0..1,0..1], shading=ZHUE, style=patchcontour, axes=BOXED );
|
![F := PIECEWISE([3^(1/2)*(y-x^(1/2)), y <= 1/2-1/2*x+1/2*x^(1/2)],[3^(1/2)*(1-x-y), 1/2-1/2*x+1/2*x^(1/2) < y])](images/Volume74.gif)
![[Maple Plot]](images/Volume75.gif)
Because each cross-section perpendicular to the x-axis is an equilateral triangle with sides of length
| > |
Ltri := bot-top:
L[tri] = Ltri;
|
![L[tri] = 1-x-x^(1/2)](images/Volume76.gif)
the height of the triangle is
| > |
Htri := sqrt(3)/2 * Ltri:
H[tri] = Htri;
|
![H[tri] = 1/2*3^(1/2)*(1-x-x^(1/2))](images/Volume77.gif)
Thus, the area of the cross-sectional triangle at
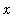 , 0 <
, 0 <
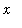 <
<
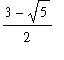 , is
, is
| > |
Atri := 1/2*Ltri*Htri:
A[tri] = Atri;
|
![A[tri] = 1/4*(1-x-x^(1/2))^2*3^(1/2)](images/Volume81.gif)
The definite integral for the volume of this solid can now be written down, and evaluated:
| > |
V4 := Int( Atri, x=0..left ):
V[tri] = V4;
`` = value( V4 );
`` = evalf( value( V4 ) );
|
![V[tri] = Int(1/4*(1-x-x^(1/2))^2*3^(1/2),x = 0 .. -1/2*5^(1/2)+3/2)](images/Volume82.gif)
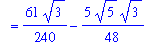

Lesson Summary
The volume of a solid can be written as a definite integral whenever the solid sliced into cross-sections with known area or peeled into shells with known surface area. For a solid of revolution the cross section is either a disk or washer and the cross-sectional area can be expressed in terms of the area of circles. The Methods of Disks and Washers are used much more often than the Method of Shells. When the Method of Shells is used, the shell are typically circular cylinders.
The definite integral for the volume of a solid by the
Method for Solid with Known Cross-Section
is
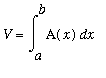 where the cross-sections have area
where the cross-sections have area
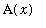 for
for
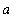 <=
<=
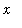 <=
<=
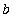 .
.
When the cross-section is a circular disk with outer radius
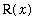 , the cross-sectional area is
, the cross-sectional area is
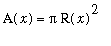 and the above formula gives the
Method of Disks
and the above formula gives the
Method of Disks
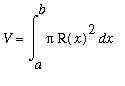 .
.
When the cross-section is a circular washer with outer radius
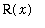 and inner radius
and inner radius
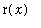 , the cross-sectional area is
, the cross-sectional area is
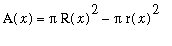 and the formula for the
Method of Washers
is obtained:
and the formula for the
Method of Washers
is obtained:
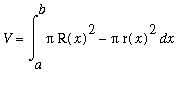 .
.
The
Method of Shells
is based on the idea of building the solid from concentric cylinders (shells). The formula
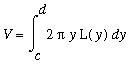
is obtained when each cylinder has the
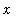 -axis as its axis, the length (height) of the cylinder is
-axis as its axis, the length (height) of the cylinder is
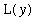 for all radii
for all radii
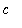 <=
<=
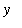 <=
<=
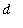 .
.
While knowing these formulae can be useful, understanding how these formulae are obtained is more important. For example, you should be able to handle situations in which the axis is not a coordinate axis.
What's Next?
The emphasis of this application is setting up the definite integral. Evaluating the integral to find a numeric (or symbolic) expression for the volume is important but this is a secondary concern. The
online homework assignment, including the practice sessions, emphasize the conceptual topics of this lesson.. Work enough practice problems to master these concepts, then complete the online homework assignment and the
assigned problems from the text. The textbook problems typically involve both the setup of the definite integral and its evaluation.
The next application is arclength - computing the
Length of a Plane Curve. This is another application that can be handled with the slice, approximate, limit, evaluate procedure.
![]() for
for
![]() <=
<=
![]() <=
<=
![]() is
is
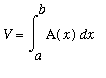 .
.
![]() -axis is
-axis is
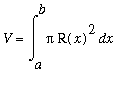 .
.
![]() for
for
![]() <=
<=
![]() <=
<=
![]() .
.
![]() -axis is
-axis is
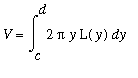 .
.
![]() is the length of the shell with radius
is the length of the shell with radius
![]() for all radii
for all radii
![]() <=
<=
![]() <=
<=
![]() .
.
![]() - or
- or
![]() -axis.
-axis.
![[Maple Plot]](images/Volume21.gif)
![V[`solid 1`] = Int(Pi*x,x = 0 .. 1)](images/Volume24.gif)
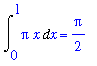
![[Maple Plot]](images/Volume35.gif)
![[Maple Plot]](images/Volume38.gif)
![[Maple Plot]](images/Volume39.gif)
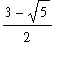 <
<
![V[`solid 2`] = Int(Pi*x-Pi*(1-x)^2,x = -1/2*5^(1/2)+3/2 .. 1)](images/Volume48.gif)
![[Maple Plot]](images/Volume57.gif)
![[Maple Plot]](images/Volume58.gif)
![V[washer] = Int((2-x)*Pi*x,x = 0 .. -1/2*5^(1/2)+3/2)+Int(Pi*(1-x),x = -1/2*5^(1/2)+3/2 .. 1)](images/Volume59.gif)
![V[shell] = Int(2*Pi*y*(y^2-1+y),y = -1/2+1/2*5^(1/2) .. 1)](images/Volume64.gif)
![[Maple Plot]](images/Volume71.gif)
![F := PIECEWISE([3^(1/2)*(y-x^(1/2)), y <= 1/2-1/2*x+1/2*x^(1/2)],[3^(1/2)*(1-x-y), 1/2-1/2*x+1/2*x^(1/2) < y])](images/Volume74.gif)
![[Maple Plot]](images/Volume75.gif)
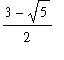 , is
, is
![A[tri] = 1/4*(1-x-x^(1/2))^2*3^(1/2)](images/Volume81.gif)
![V[tri] = Int(1/4*(1-x-x^(1/2))^2*3^(1/2),x = 0 .. -1/2*5^(1/2)+3/2)](images/Volume82.gif)
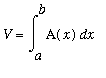 where the cross-sections have area
where the cross-sections have area
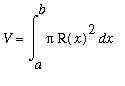 .
.
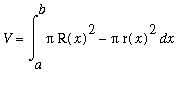 .
.