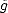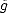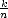Elements of Approximation Theory:
Constructive Approximation and Examples
*Department of Mathematics, Purdue University
|
Abstract
In this survey we introduce the general Theory of Approximation to functions in (quasisemi)normed
spaces; the exposition starts with an explanation of the main problem: we impose certain family
of subspaces as our approximants, and we need to obtain a description of the subspace(s) that are
approximated by this family with a given approximation order. We introduce as well to some of the
background and basic tools most often used to solve this kind of problems. Approximation Theory
gets heavily improved when some efforts are put into the effective construction of the approximants
on each given example, rather than simply stating its existence --this is what we call “Constructive
Approximation”. The fact that we can handle actual functions, allows us to obtain yet more properties
of the approximants. It is implicit throughout the exposition how Approximation Theory benefits from
other branches of Mathematics, but also how Constructive Approximation can be used to prove results
from those other subjects. Finally, we include extensive examples that help us better understand how all
this can be achieved.
|
Contents
1 Approximation Theory
1.1 Introduction
Let (X,||.||X) be a (quasisemi)normed linear space. Consider a countable family of spaces in X, {Xn}n with
associated error functionals E(.,Xn)X = inf g Xn||.-g||X, satisfying the following properties:
Xn||.-g||X, satisfying the following properties:
- Homogeneity:
 Xn = Xn for all n and
Xn = Xn for all n and 


- C-linearity: There exists C > 1 (independent of n) such that Xn + Xn = XCn for all n.
- Local (near)best approximation: Given f
 X, there exists an element of (near)best approximation to f from
Xn for all n.
X, there exists an element of (near)best approximation to f from
Xn for all n.
- Global best approximation: limnE(f,Xn)X = 0 for all f
 X.
X.
We will call {Xn} a family of approximants. For any such family, and given parameter values  ,q > 0, consider
the following (quasi)seminorms and associated subspaces:
,q > 0, consider
the following (quasi)seminorms and associated subspaces:
We call these Approximation Spaces associated to the family of approximants {Xn}. They consist on those functions
f  X that are approximated in X by elements of Xn with error of order O(
X that are approximated in X by elements of Xn with error of order O( ) (i.e. , there exists C > 0 such that
E(f,Xn)X < Cn-
) (i.e. , there exists C > 0 such that
E(f,Xn)X < Cn- for all n) and “smoothness” q.
for all n) and “smoothness” q.
Lemma 1.1 If the sequence 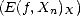 n is monotone decreasing, then the (quasi)seminorms |.|Aq
n is monotone decreasing, then the (quasi)seminorms |.|Aq (X,Xn) are
equivalent to the following:
(X,Xn) are
equivalent to the following:
Proof. For any k > 0 and any 2k-1 < n < 2k, we have the estimates
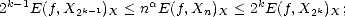 therefore, and similarly,
therefore, and similarly,
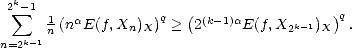 Adding all the terms of the series that defines the seminorm associated to the spaces Aq
Adding all the terms of the series that defines the seminorm associated to the spaces Aq (X,Xn), and applying the
estimates above, we get the desired result.
(X,Xn), and applying the
estimates above, we get the desired result. ![[#]](msam10-4.gif)
Proof. This is just an application of the well known inclusions  q
q 
 p for 0 < q < p <
p for 0 < q < p < : Consider the measure
space (
: Consider the measure
space (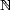 ,
,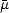 ), where
), where 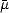 (n) = 1 for all n, and consider for each function f
(n) = 1 for all n, and consider for each function f  X the (measurable in (
X the (measurable in (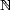 ,
,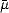 )) functions
)) functions
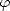
 :
: 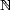
 k
k 2k
2k E(f;X2k)X
E(f;X2k)X 
 +; then,
+; then,
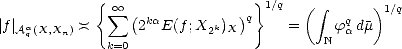 If
f
If
f  Aq
Aq , then certainly
, then certainly 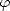


 q
q 

 , and therefore;
, and therefore;
![(i ntegral )1/p
|f| a )( fp dm < ||f || ||f || )( |f |a | f |a [#]
A p(X,Xn) N a a l oo a lq A oo (X,Xn) Aq(X,Xn)](root12x.gif)
Remark. In the following sections we will learn to find descriptions of these spaces in terms of classical spaces. The
main tools used in this sense are given in the following order:
- The (quasi)seminorms (1.1), (1.2), (1.3) and (1.4) are discretizations of p-norms over
 + with the Haar
measure dx/x. We have included some useful results related to these measures in §1.2.
+ with the Haar
measure dx/x. We have included some useful results related to these measures in §1.2.
- §1.3 deals with the existence and properties of general (abstract) best and near-best approximations.
- Both §1.4 and §1.5 introduce us to Interpolation Spaces and how these are related to our problem of
approximation via Jackson and Bernstein’s inequalities.
1.2 Hardy’s Inequalities
Proof. Let us prove the estimate (1.5). For any value  > 0 we estimate first the interior integral using Hölder’s
Inequality; let p be the conjugate exponent of q:
> 0 we estimate first the interior integral using Hölder’s
Inequality; let p be the conjugate exponent of q:
![integral integral (i ntegral )1/q( integral )1/p
tf(s)ds = ts- cf(s)sc-1ds < t[s-cf(s)]qds tsp(c- 1)ds
0 s 0 0 0](root15x.gif) The
second integral can be computed provided
The
second integral can be computed provided  < 1; in that case we obtain
< 1; in that case we obtain
![integral t- p(1-c) 1-p(1-c)]t
s ds = Cq,c s s=0
0](root16x.gif) and if
and if
 > 1/q, we have
> 1/q, we have 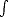 0ts-p(1-
0ts-p(1- )ds = Cq,
)ds = Cq, t1-p(1-
t1-p(1- ). We can then estimate the left-hand side of (1.5) using this result
and a change in the order of integration: The latter integral can be computed provided
). We can then estimate the left-hand side of (1.5) using this result
and a change in the order of integration: The latter integral can be computed provided  < 1/q +
< 1/q +  ; we get in that case
; we get in that case
![integral oo [ integral t ]q integral oo
t-a f(s)ds dt < Cq,a,c [s-af(s)]q ds
0 0 s t 0 s](root18x.gif) In
order to get rid of the dependence of
In
order to get rid of the dependence of  in the constant, we may choose this parameter so that it depends solely on
in the constant, we may choose this parameter so that it depends solely on  and q, besides satisfying the constraints we have imposed. The obvious choice is
and q, besides satisfying the constraints we have imposed. The obvious choice is  = 1/q +
= 1/q +  /p, and in that case we
get trivially Cq,
/p, and in that case we
get trivially Cq, =
=  -q.
-q.
The remaining estimates can be obtained from this one by changes of variable or taking limits, so we skip their
proofs. ![[#]](msam10-4.gif)
Remark. It is possible to discretize integrals of the kind 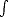 0
0
![[t-af(t)]](root19x.gif) q
q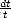 when the functions
when the functions 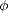 (t) are nonnegative
and monotone, using the same technique we used in the proof of Lemma 1.1:
(t) are nonnegative
and monotone, using the same technique we used in the proof of Lemma 1.1:
![integral oo [ ]q dt sum integral 2k+1[ ]q dt sum
t-af(t) t-= k t- af(t) -t )( 2aqkf(2-k)q.
0 k (- Z 2 k (- Z](root21x.gif) Associated to this discrete functional, we have the following result, that will allow us to extend the previous theorem
to 0 < p < 1 for nonnegative monotone functions.
Associated to this discrete functional, we have the following result, that will allow us to extend the previous theorem
to 0 < p < 1 for nonnegative monotone functions.
Proof. Let us assume that the first condition is satisfied. From the inclusions 



 for 0 <
for 0 <  <
<  <
< , we infer
that it must also be bn
, we infer
that it must also be bn < C0
< C0 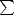 k=n
k=n ak
ak for all
for all  <
<  . We can therefore assume that
. We can therefore assume that  < q (if it is not, then we
can certainly pick
< q (if it is not, then we
can certainly pick  < q <
< q <  ). We are now able to use Hölder’s Inequality; let 0 <
). We are now able to use Hölder’s Inequality; let 0 < 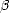 <
<  , and let r > 0 so that
, and let r > 0 so that
 /q +
/q +  /r = 1:
/r = 1:
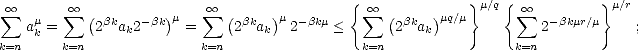 therefore,
therefore,
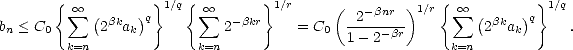 We
have then As in the proof of the previous Theorem, we may choose
We
have then As in the proof of the previous Theorem, we may choose 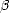 depending only on
depending only on  , and
, and  depending solely on q, hence
narrowing the dependence of the constants on parameters.
depending solely on q, hence
narrowing the dependence of the constants on parameters.
A similar proof serves to show that the second condition also gives the same estimate, but this time only for values
0 <  <
<  .
. ![[#]](msam10-4.gif)
Proof. Given t > 0, there exists n 
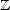 such that 2-(n+1) < t < 2-n; therefore,
such that 2-(n+1) < t < 2-n; therefore,
Denote bn = 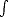 02-n
02-n
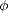 (s)
(s) , an =
, an =  (2-n), and use the previous lemma to estimate the integral in the left-hand side of
(1.9): With the same technique, we find an upper estimate on the right-hand side of (1.9) in the same terms:
(2-n), and use the previous lemma to estimate the integral in the left-hand side of
(1.9): With the same technique, we find an upper estimate on the right-hand side of (1.9) in the same terms:
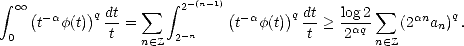 This
gives us the first estimate. For the second, a change of variables in this one suffices.
This
gives us the first estimate. For the second, a change of variables in this one suffices. ![[#]](msam10-4.gif)
1.3 Best and Near-Best Approximation
Lemma 1.4 Let (
X,d)
be a metric space and let Y be a compact subset of X; then for each f  X there
exists an element of best approximation to f from Y .
X there
exists an element of best approximation to f from Y .
Proof. Consider for each n 
 an element gn
an element gn  Y such that d(f,gn) < inf g
Y such that d(f,gn) < inf g Y d(f,g) + 1/n. Any sequence in a
compact set has at least a limit element g0
Y d(f,g) + 1/n. Any sequence in a
compact set has at least a limit element g0  Y ; this element is the best approximation to f from Y by definition.
Y ; this element is the best approximation to f from Y by definition. ![[#]](msam10-4.gif)
Theorem 3 Let X be a (quasi)normed space. For each finite dimensional subspace Xd of X and each
f  X, there is a best approximation to f from Xd.
X, there is a best approximation to f from Xd.
Proof. If Xd = {0} then there is nothing to prove. Otherwise, consider for each f  X the set
Y f =
X the set
Y f = 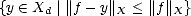 . Y f is a closed set:
. Y f is a closed set:
![-1
Yf = F (- oo , ||f||X], where F : Y -) y '--> ||f - y|| X (- R](root33x.gif) Y f is
also bounded, since for any y
Y f is
also bounded, since for any y  Y f,
Y f,
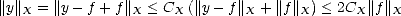 By
Corollary 27.1 (page 101), it must be Y f compact, and therefore a best approximation from Y f exists.
By
Corollary 27.1 (page 101), it must be Y f compact, and therefore a best approximation from Y f exists. ![[#]](msam10-4.gif)
Proof. Given x,y  X, assume E(x-y,Z)X < E(y,Z)X (it’s not a lost of generality, since one can switch elements).
Let z
X, assume E(x-y,Z)X < E(y,Z)X (it’s not a lost of generality, since one can switch elements).
Let z  Z be a
Z be a  near-best approximation to x from Z, and z'',z'''
near-best approximation to x from Z, and z'',z''' Z elements of best approximation from Z to
y - x and y respectively. We have then for z' = z'' + z,
Z elements of best approximation from Z to
y - x and y respectively. We have then for z' = z'' + z,
Definition 2 A subset Y of a (quasi)normed space X is said to be a unicity space, if for each f  X there
exists a unique element of best approximation from Y .
X there
exists a unique element of best approximation from Y .
Example. The spaces Lp are unicity spaces for 1 < p <  , but not for 0 < p < 1 nor p =
, but not for 0 < p < 1 nor p =  . A characterization of
spaces (at least normed) with the unicity property can be made through the use of “strict convexity”:
. A characterization of
spaces (at least normed) with the unicity property can be made through the use of “strict convexity”:
Definition 3 A normed space is said to be strictly convex if the following property holds:
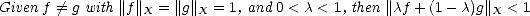
Lemma 1.6 If X is strictly convex, then the best approximation is unique.
Proof. Assume the result is not true, and there exists a function f  X and two different elements g1,g2
X and two different elements g1,g2  Y such
that ||f - g1||X = ||f - g2||X = E(f,Y )X > 0. In that case,
Y such
that ||f - g1||X = ||f - g2||X = E(f,Y )X > 0. In that case,
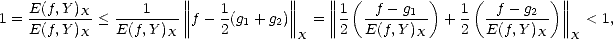 a
contradiction.
a
contradiction. ![[#]](msam10-4.gif)
Proposition 1 Given a finite dimensional unicity subspace Xd  X, the operator of best approximation is
continuous.
X, the operator of best approximation is
continuous.
Proof. Let 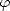 : X
: X  X the operator of best approximation, and let CX > 1 be the constant in the (quasi)triangular
inequality offered by the (quasi)norm ||.||X. Given
X the operator of best approximation, and let CX > 1 be the constant in the (quasi)triangular
inequality offered by the (quasi)norm ||.||X. Given  > 0, let
> 0, let 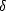 =
=  (3CX2)-1. Notice that, if f,g
(3CX2)-1. Notice that, if f,g  X verify
||f - g||X <
X verify
||f - g||X < 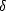 , then we have
, then we have
1.4 Interpolation Spaces: The Real Method
Definition 4 A compatible couple is a pair of (quasisemi)normed linear spaces, (X,||.||X), and (Y,||.||Y )
continuously embedded in a Hausdorff topological linear space H.
We define the sum and intersection of such a couple as
Definition 5 Given a compatible couple (
X,Y )
, we say a linear operator T :
X +
Y  X
X +
Y is admisible
for the couple if
(i) T(
X)
 X, and
X, and 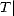 X is bounded.
(ii) T
X is bounded.
(ii) T(
Y )
 Y , and
Y , and 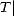 Y is bounded.
Y is bounded.
Definition 6 A (quasisemi)normed linear space (
Z,||.||Z)
is intermediate between
X and
Y (or for the
couple given by those spaces), if
(i) X  Y
Y 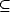 Z
Z 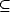 X
X +
Y
(ii) X  Y is continuously embedded in Z: there exists CX
Y is continuously embedded in Z: there exists CX Y >
Y > 0
such that ||f||Z < CX Y ||f||X
Y ||f||X Y for all
f
Y for all
f  X
X  Y .
(iii) Z is continuously embedded in X
Y .
(iii) Z is continuously embedded in X +
Y : there exists CX+Y > 0
such that ||f||X+Y < CX+Y ||f||Z for all
f  Z.
Z.
An intermediate space Z of a compatible couple (X,Y ) is an interpolation space for the couple if T(Z)  Z
for all admisible operator T.
Z
for all admisible operator T.
Remark. In the 70’s there were primaryly two methods for constructing interpolation spaces of a compatible
couple: the complex method of Calderón [Cal1], and the real method of Lions and Peetre [Peet]. We are mainly
interested in the latter, since it uses as building blocks similar quasi-seminorms to the ones in the description of the
Approximation Spaces above.
Definition 7 We define the K-functional of a compatible couple (X,Y ) as follows:
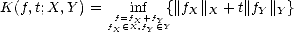 for each f
for each f  X
X +
Y and t > 0
.
Lemma 1.7 (Properties of the K-functional) Let (
X,Y )
be a compatible couple:
(i) K(
f,.;
X,Y )
is a continuous subadditive convex-down monotone nondecreasing function of t that verifies
K(
f,t;
X,Y ) =
tK(
f,q/t;
Y,X)
, and K(
f,nt;
X,Y )
< nK(
f,t;
X,Y )
for all n 
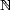 and t >
and t > 0
.
(ii) For each t > 0
, K(
.,t;
X,Y )
is a (quasi)seminorm equivalent to ||.||X+Y .
(iii) Let (
X,Y )
be a compatible couple and let T be an admisible operator; then for each f  X
X +
Y and
t > 0
,
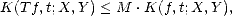 where M
where M = max
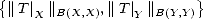 .
.
Proof. Notice that, given f  X + Y , the function K(f,.;X,Y ) is trivially nonnegative and monotone
nondecreasing. Its concavity is proved in the following way: Given t1,t2 > 0 and 0 <
X + Y , the function K(f,.;X,Y ) is trivially nonnegative and monotone
nondecreasing. Its concavity is proved in the following way: Given t1,t2 > 0 and 0 <  < 1, and any decomposition
f = fX + fY , we have, for t =
< 1, and any decomposition
f = fX + fY , we have, for t =  t1 + (1 -
t1 + (1 -  )t2,
)t2,
(a more intuitive way to see that K(f,.;X,Y ) is indeed a convex down function is to realize that we construct it as
the infimum of lines with slopes ||fY ||Y and y-interceptions ||fX||X, where the previous functions come from the
obvious decompositions of f in X + Y )
The identity K(f,t;X,Y ) = tK(f,1/t;Y,X) is also trivial:
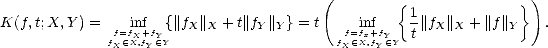 The
subadditivity follows from the previous identity; let g(s) = K(f,1/s;X,Y ) = K(f,s;X,Y )/s. As K(f,s;X,Y ) is
nondecreasing, g must be nonincreasing, and therefore, if t1,t2 > 0 From the last estimate, we find K(f,nt;X,Y ) < nK(f,t;X,Y ) trivially. The continuity also follows from the
subadditivity, since given h > 0,
The
subadditivity follows from the previous identity; let g(s) = K(f,1/s;X,Y ) = K(f,s;X,Y )/s. As K(f,s;X,Y ) is
nondecreasing, g must be nonincreasing, and therefore, if t1,t2 > 0 From the last estimate, we find K(f,nt;X,Y ) < nK(f,t;X,Y ) trivially. The continuity also follows from the
subadditivity, since given h > 0,
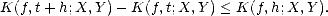 To
prove property (ii), we realize first that both nonnegativity and homogeneity of K(.,t;X,Y ) are trivial. Let
C = max{CX,CY } > 0 (associated to the constants from the definition of the (quasisemi)norms of X and Y ); then,
for each f,g
To
prove property (ii), we realize first that both nonnegativity and homogeneity of K(.,t;X,Y ) are trivial. Let
C = max{CX,CY } > 0 (associated to the constants from the definition of the (quasisemi)norms of X and Y ); then,
for each f,g  X + Y and any decomposition f = fX + fY , g = gX + gY :
X + Y and any decomposition f = fX + fY , g = gX + gY :
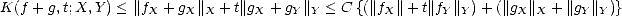 The
equivalence of K(.,t) with ||.||X+Y comes from:
The
equivalence of K(.,t) with ||.||X+Y comes from:
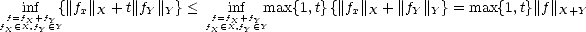 The
other estimate is similar.
The
other estimate is similar.
Let us prove now (iii): Given f  X + Y , decompose f = fX + fY and notice that
X + Y , decompose f = fX + fY and notice that
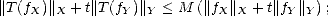 therefore, K(Tf,t;X,Y ) < M
therefore, K(Tf,t;X,Y ) < M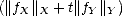 , which proves the desired result.
, which proves the desired result. ![[#]](msam10-4.gif)
Lemma 1.8 Given a compatible couple (
X,Y )
, and parameters 0
<  <
< 1
, 0
< q < , the following functionals are
(quasi)seminorms in X
, the following functionals are
(quasi)seminorms in X +
Y :
Proof. |.|(X,Y ) ,q is trivially linear and nonnegative. The (quasi)triangular inequality is directly inferred from part
(ii) in Lemma 1.7.
,q is trivially linear and nonnegative. The (quasi)triangular inequality is directly inferred from part
(ii) in Lemma 1.7. ![[#]](msam10-4.gif)
Proof. This is inmediate from (iii) in Lemma 1.7. ![[#]](msam10-4.gif)
Proof. Part (i) is trivial. As for part (ii), we start noticing that
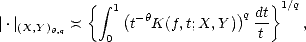 since
for each g
since
for each g  Y , K(f,t;X,Y ) <||f||X < C
Y , K(f,t;X,Y ) <||f||X < C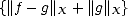 < C
< C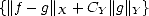 , and therefore,
K(f,t;X,Y ) < C K(f,CY ;X,Y ) for all t > 0. So, we can estimate (for 0 < q <
, and therefore,
K(f,t;X,Y ) < C K(f,CY ;X,Y ) for all t > 0. So, we can estimate (for 0 < q <  )
)
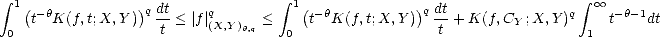 Now,
due to the monotonicity of the K-functional, we can discretize the previous integral, with an argument similar to the
one employed in the proof of Lemma 1.1 (page 5).
Now,
due to the monotonicity of the K-functional, we can discretize the previous integral, with an argument similar to the
one employed in the proof of Lemma 1.1 (page 5). ![[#]](msam10-4.gif) Remark. Notice how similar this (quasi)seminorms are to the ones in Lemma 1.1. One of the tricks in
Approximation Theory is, given (X,||.||X) and a family of approximants {Xn}n, find a continuously embedded
(quasisemi)normed subspace (Y,||.||Y )
Remark. Notice how similar this (quasi)seminorms are to the ones in Lemma 1.1. One of the tricks in
Approximation Theory is, given (X,||.||X) and a family of approximants {Xn}n, find a continuously embedded
(quasisemi)normed subspace (Y,||.||Y )  X so that the values E(f,Xn)X can be estimated in terms
of the K-functionals K(f,2m;X,Y ) and viceversa. In §1.5 we outline some results that help in this
sense.
X so that the values E(f,Xn)X can be estimated in terms
of the K-functionals K(f,2m;X,Y ) and viceversa. In §1.5 we outline some results that help in this
sense.
Another important result related to K-functionals and the ( ,q) interpolation spaces is the Reiteration Theorem,
that states that no advantage is gained when applying succesive interpolation to a given compatible couple.
,q) interpolation spaces is the Reiteration Theorem,
that states that no advantage is gained when applying succesive interpolation to a given compatible couple.
Theorem 4 (Holmsted (1970)) Let (X1,||.||X1), (X2,||.||X2) be a compatible couple of (quasi)normed
spaces, let 0 <  1 <
1 <  2 < 1 and 0 < q1,q2 <
2 < 1 and 0 < q1,q2 <  , and consider the interpolation spaces Y 1 = (X1,X2)
, and consider the interpolation spaces Y 1 = (X1,X2) 1,q1,
Y 2 = (X1,X2)
1,q1,
Y 2 = (X1,X2) 2,q2; then, for f
2,q2; then, for f  Y 1 + Y 2 and
Y 1 + Y 2 and 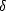 =
=  2 -
2 -  1, we have the following equivalence:
1, we have the following equivalence:
![( integral t )1/q1 (i ntegral oo )1/q2
K(f, td;Y1,Y2) )( [s-a1K(f,s;X1,X2)]q1 ds + td [s-a2K(f,s;X1,X2)]q2 ds ,
0 s t s](root61x.gif) with constants of equivalency independent of f and t. The usual change from integral to a supremum applies
when either q1 or q2 are infinite.
with constants of equivalency independent of f and t. The usual change from integral to a supremum applies
when either q1 or q2 are infinite.
Theorem 5 (Peetre’s Reiteration Theorem (1963)) Under the same hypothesis as the previous
Theorem, and for any 0
<  <
< 1
, 0
< q < , we have
, we have (
Y 1,Y 2)
 ,q
,q = (
X1,X2)
 ',q, where
',q, where  '
' = (1
-
)
 1
1+

 2.
2.
1.5 Jackson and Bernstein Inequalities
Definition 8 Given a (quasisemi)normed space (X,||.||X), and (quasisemi)normed continuously embedded
subspace (Y,|.|Y )  X,
Jackson Inequality: We say the family of approximants {Xn}n verifies a Jackson Inequality with respect to
Y if there exist r,C > 0 such that
X,
Jackson Inequality: We say the family of approximants {Xn}n verifies a Jackson Inequality with respect to
Y if there exist r,C > 0 such that
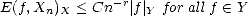 Bernstein Inequality: We say the family of approximants {Xn}n verifies a Bernstein inequality with respect
to Y if there exist r,C >
Bernstein Inequality: We say the family of approximants {Xn}n verifies a Bernstein inequality with respect
to Y if there exist r,C > 0
such that
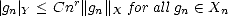
Remark. In the literature of Approximation Theory, results that state Jackson’s Inequalities are
refered as “direct theorems”, whereas Bernstein’s inequalities are also identified as “inverse theorems”.
Proposition 3 Given a (quasisemi)normed space (X,||.||X), a family of approximants {Xn}n satisfying both
Jackson and Bernstein inequalities with respect to a (quasisemi)normed continuously embedded linear subspace
(Y,|.|Y )  X, the following estimates hold:
X, the following estimates hold:
Proof. To prove (1.11), given f  X, consider any g
X, consider any g  Y and a best approximation gn to g in X from each Xn; then,
Y and a best approximation gn to g in X from each Xn; then,
therefore proving property (1.11) (use part (i) of Lemma 1.7, page 18). To prove (1.12), denote gk the best
approximation to f from X2k, and 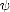 k = gk - gk-1. We know that there exists a constant C > 0 such that
Xn + Xn = XCn for all n; this means in particular that
k = gk - gk-1. We know that there exists a constant C > 0 such that
Xn + Xn = XCn for all n; this means in particular that 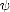 k
k  X2kC for all k, and by the Bernstein property,
|
X2kC for all k, and by the Bernstein property,
|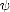 k|Y < 2krC||
k|Y < 2krC||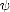 k||X. But now,
k||X. But now,
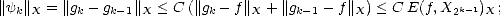 We
have then the estimate |
We
have then the estimate |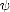 k|Y < 2krC E(f,X2k-1)X, which we can use to estimate the K-functional:
Remark. This last result allows the link we were looking for between Interpolation and Approximation
Theories. The following three results give a very good example: Corollary 3.1 tells us that the problem of
characterizing approximation spaces by means of interpolation spaces is solved if we know two ingredients:
k|Y < 2krC E(f,X2k-1)X, which we can use to estimate the K-functional:
Remark. This last result allows the link we were looking for between Interpolation and Approximation
Theories. The following three results give a very good example: Corollary 3.1 tells us that the problem of
characterizing approximation spaces by means of interpolation spaces is solved if we know two ingredients:
- An appropriate (quasisemi)normed linear subspace (Y,|.|Y )
 X for which the family of approximants
{Xn}n verifies the Jackson and Bernstein inequalities.
X for which the family of approximants
{Xn}n verifies the Jackson and Bernstein inequalities.
- A characterization of the interpolation spaces (X,Y )
 ,q.
,q.
The second step is often provided by classical results in the Theory of Interpolation. The first step is the
difficult one from the viewpoint of approximation. Theorem 6 provides a good start. Finally, Theorem
7 (proof not offered here, read it in [CDeH]) provides somehow an inverse result to Corollary 3.1.
Proof. Estimate (1.11) gives us Aq (X,Xn)
(X,Xn)  (X,Y )
(X,Y ) /r,q trivially; for example, for 0 < p <
/r,q trivially; for example, for 0 < p <  , and r that makes
good both Jackson’s and Bernstein’s Inequalities, if f
, and r that makes
good both Jackson’s and Bernstein’s Inequalities, if f  (X,Y )
(X,Y ) /r,q, then
/r,q, then
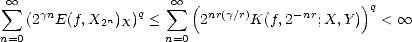 On
the other hand, we may use estimate (1.12) into Lemma 1.3 (page 10) to realize the other inclusion: Let
bn = K(f,2-nr;X,Y ), an = E(f,X2n)X, and 0 <
On
the other hand, we may use estimate (1.12) into Lemma 1.3 (page 10) to realize the other inclusion: Let
bn = K(f,2-nr;X,Y ), an = E(f,X2n)X, and 0 < 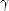 < r; we have then
< r; we have then
Proof. It is enough to show that {Xn}n verifies both Jackson and Bernstein’s Inequalities for the exponent r > 0
with respect to Apr(X,Xn):
- Let f
 Apr(X,Xn); we know that there exists C > 0 such that
Apr(X,Xn); we know that there exists C > 0 such that
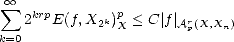 Given n, find k such that 2k < n < 2k+1; then,
Given n, find k such that 2k < n < 2k+1; then,
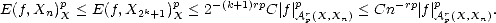
- Given gn
 Xn, we have
Xn, we have
The rest of the statement follows inmediatelly. ![[#]](msam10-4.gif)
2 Dyadic maximal-smoothness Spline Approximation
In this section we want to exemplify how to obtain the approximation spaces in the following case: Given the
unit cube 

 d, X = Lp(
d, X = Lp( ) for any choice of 0 < p <
) for any choice of 0 < p < , and Xn is a linear space of box-splines
with coordinate order r, maximal smoothness, and associated to the dyadic n-th partition of the cube
, and Xn is a linear space of box-splines
with coordinate order r, maximal smoothness, and associated to the dyadic n-th partition of the cube
 .
.
In the search for the spaces Aq (X,Xn), we will go through different levels of abstraction: from the low-level
construction of best and near-best polynomial approximation to functions in Lp(
(X,Xn), we will go through different levels of abstraction: from the low-level
construction of best and near-best polynomial approximation to functions in Lp( ) on cubes, to the high-level
description of the K-functionals that will lead us into further results involving interpolation spaces for
compatible couples of Besov spaces. The logic step-by-step exposition is summarized in the following
table:
) on cubes, to the high-level
description of the K-functionals that will lead us into further results involving interpolation spaces for
compatible couples of Besov spaces. The logic step-by-step exposition is summarized in the following
table:
- Basic Pre-requisites:
- Construction and results on different norm estimations related to best and near best Lp(
 )
polynomial approximation in subcubes (§2.1).
)
polynomial approximation in subcubes (§2.1).
- Markov’s Theorem on norm extimation of derivatives of polynomials over compact intervals of
the real line (§2.2).
- Construction of the approximants and projectors:
- Divided differences: definition and basic results (§2.3).
- Univariate splines: definition, properties and description of the quasi-interpolants as projectors
associated to the construction of the puB-spline basis (§2.4).
- Multivariate tensor-product puB-splines associated to dyadic partitions of the unit cube
 , the
linear spaces spanned by them, and the generalized quasi-interpolant for these spaces (§2.5).
, the
linear spaces spanned by them, and the generalized quasi-interpolant for these spaces (§2.5).
- Search for good candidates for approximation spaces:
- Sobolev Spaces (§2.6).
- Besov Spaces (§2.7).
- Solution of the problem of approximation and related results:
- Construction of equivalent seminorm functionals for Besov Spaces that link them with the
approximation spaces we are looking for (§2.8).
- Interpolation of compatible couples of Besov Spaces (sections 2.9, 2.10 and 2.11).
- Embedding Theorems for Besov Spaces (§2.12).
2.1 Best and Near-Best Lp Polynomial Approximation in cubes of  d
d
Proof. Consider for all p > 0 the (quasi)norms |||.|||Lp( ) = |
) = | |-1/p||.||Lp(
|-1/p||.||Lp( ) in
) in  (r), and apply Theorem 27 (page
101).
(r), and apply Theorem 27 (page
101). ![[#]](msam10-4.gif)
Proof. Consider the (quasi)norms ||.||I,Lq( ) = |I|-1/q||.||Lq(
) = |I|-1/q||.||Lq( ) in
) in  (r) and apply Theorem 27 again.
(r) and apply Theorem 27 again. ![[#]](msam10-4.gif)
Proof. Let P be the best Lp( ) approximation element to f from
) approximation element to f from  (r); then we have:
(r); then we have:
Proof. Let P be the best Lp(J) approximation element to f from  (r). First, notice that for any cube I
(r). First, notice that for any cube I  J,
J,
This estimate is all we need to finish the proof:
2.2 Markov’s Theorem
Theorem 8 (Szegö (1928)) For each trigonometric polynomial Tr of order r,
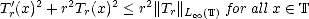
Corollary 8.1 (Bernstein’s Inequalities)
||T'r||L (
( ) < r||Tr||L
) < r||Tr||L (
( ).
||Tr(k)||L
).
||Tr(k)||L (
( ) < rk||Tr||L
) < rk||Tr||L (
( ).
).
Corollary 8.2 For an algebraic polynomial Pr 

(
r)
, and all x 
(
-1
,1)
,
![|P'r(x)| < r||P V~ r||L oo [--1,1].
1- x2](root82x.gif)
Corollary 8.3 For an algebraic polynomial Pr 


(
r)
of order r with complex coefficients on the disk
D =
{z 
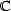
:
|z|< 1
},
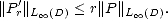
Theorem 9 (Markov) For an algebraic polynomial Pr 

(
r)
,
![||P'r||L oo [- 1,1] < r2|| Pr||L oo [-1,1].](root84x.gif)
2.3 Divided Differences
Lemma 2.5 (Newton’s Interpolation polynomial) Given a function f :


 , and knots t0 < ... <
tn, the interpolation polynomial of f at those knots, Pf
, and knots t0 < ... <
tn, the interpolation polynomial of f at those knots, Pf(
x;
t0,...,tn)
can be written in terms of the divided
differences as follows:
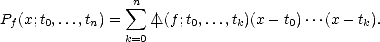
Proof. Given f : 

 , consider the following interpolation polynomials for each k = 0,...,n - 1:
Qk(x) = Pf(x;t0,...,tk)
, consider the following interpolation polynomials for each k = 0,...,n - 1:
Qk(x) = Pf(x;t0,...,tk) 
 (k), Qk+1(x) = Pf(x;t0,...,tk+1)
(k), Qk+1(x) = Pf(x;t0,...,tk+1) 
 (k + 1). Notice that g = Qk+1 - Qk
(k + 1). Notice that g = Qk+1 - Qk 
 (k + 1)
vanishes at the knots t0,...,tk, and by definition its leading coefficient is the divided difference |
(k + 1)
vanishes at the knots t0,...,tk, and by definition its leading coefficient is the divided difference |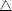 (f;t0,...,tk+1);
hence,
(f;t0,...,tk+1);
hence,
![Pf(x;t0,...,tk+1) = Pf(x;t0,...,tk)+ | /_\ (f;t0,...,tk+1)(x- t0)...(x - tk). [#]](root87x.gif)
Lemma 2.6 If f  Cn
Cn[
a,b]
and a < tk < b for all k = 0
,...,n, then there exists 

(
a,b)
such that
|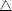
(
f;
t0,...,tn) =
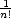 f(n)
f(n)(

)
.
Proof. This is a direct consequence of Rolle’s Theorem. ![[#]](msam10-4.gif)
Lemma 2.7 (Leibnitz Formula for Divided Differences) Given functions f,g and knots t0, ..., tn, the n-th
divided difference of their product is given by the following formula:
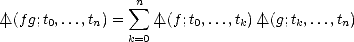 | (2.1) |
Proof. Assume all the knots are different; consider the polynomial of interpolation of h = fg at those knots (using
Newton’s expression with the divided differences as coefficients).
Notice now that the leading coefficient of Ph(x;t0,...,tn) is |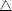 (fg;t0,...,tn), and the leading coefficient of the
expression in (2.2) is the right-hand side of (2.1).
(fg;t0,...,tn), and the leading coefficient of the
expression in (2.2) is the right-hand side of (2.1). ![[#]](msam10-4.gif)
2.4 Univariate Splines
2.4.1 Definition and Basic Properties
Definition 10 (Schoenberg spaces: knots-multiplicity form) Given a interval A = [a,b] in  , we
define initially spaces of splines in the following way: Fix r > 0 and let {a < t1 < t2 <
, we
define initially spaces of splines in the following way: Fix r > 0 and let {a < t1 < t2 <  < tn < b} be a
partition of the interval, and associated to these knots, multiplicities 0 < mk < r. We denote t = (t1,...,tn),
m = (m1,...,mn), and
< tn < b} be a
partition of the interval, and associated to these knots, multiplicities 0 < mk < r. We denote t = (t1,...,tn),
m = (m1,...,mn), and
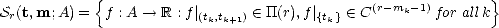 The multiplicity mk indicates the degrees of freedom (associated to polynomials with order r) on each knot
tk; hence, r-mk-
The multiplicity mk indicates the degrees of freedom (associated to polynomials with order r) on each knot
tk; hence, r-mk-1
gives the smoothness of the spline function at those points (-1
meaning discontinuity).
Classically, these are called Schoenberg spaces on A.
Remarks. For instance, m = 1 gives one degree of freedom: the location of the image of f(t). In that case, the
smoothness of f at t is r - 1, which is the maximum possible degree. In particular, this shows that
 (r) = Sr(t,1;A), where 1 = (1,...,1).
(r) = Sr(t,1;A), where 1 = (1,...,1).
On the other hand, if m = r, then we have all possible degrees of freedom: we can choose location, and all
derivatives (both sides); this leaves us piecewise polynomials with possible discontinuities on each
knot.
With a slight abuse of notation, we can write Sr(t,r;A) =  k=1n
k=1n (r)|(tk,tk+1), where r = (r,...,r).
(r)|(tk,tk+1), where r = (r,...,r).
Proposition 4 The space Sr(t,m;[a,b]) has the basis
where x+
=
x
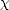 {x>0} denotes truncated powers. The associated dual functionals are as follows: In particular,
{x>0} denotes truncated powers. The associated dual functionals are as follows: In particular, dim
Sr(
t,m;[
a,b]) =
r +
|m| =
r +
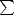 k=1nmk.
k=1nmk.
Definition 11 (Schoenberg spaces: basic knots form) Given an interval A = [
a,b]
in the real line,
r > 0
and an increasing sequence of knots t =
{a < t1 < < tn < b}, where tk < tk+r for all k, we define
the Schoenberg space Sr
< tn < b}, where tk < tk+r for all k, we define
the Schoenberg space Sr(
t;
A)
to be the space of splines of order r with knots given by the partition generated
by t, and multiplicities given by the number of repetitions of each knot in the sequence.
Example. Consider A = [0,1] and the basic knot sequence t = {0,0,0,1/2,1/2,/12,1,1,1}. In this case, we
have
![Sr(t;[0.1]) = Sr({0,1/2,1},{3,3,3};[0,1]).](root96x.gif)
Lemma 2.8 (Properties of puB-splines)
(i) N is a spline function.
(ii) supp(
Nk,r) = [
tk,tk+r]
(iii) Recurrence formula:
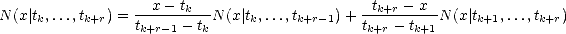
Proof. Notice that N is by definition a linear combination of truncated powers (tj - x)+r-kj, where kj is the
number of repetitions ti = tj for i < j; therefore, it is a spline function. Furthermore, since any r-th order divided
difference of a polynomial of degree r - 1 is zero, Nk,r vanishes identically when x < tk and x > tk+r (think leading
coefficients).
The recurrence formula is a direct consecuence of the recurrence formula for divided differences and Leibnitz
formula for the divided difference of a product of two functions:
therefore, proving our last statement. ![[#]](msam10-4.gif)
Remarks. On his classnotes [deBo], Carl de Boor expresses the previous recurrence formula in the following way:
where
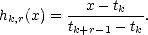 This
allows computation of puB-splines following a Horner’s scheme-like method, and actually it can be used
as startpoint of the development of the theory of B-splines, rather than using divided differences.
This
allows computation of puB-splines following a Horner’s scheme-like method, and actually it can be used
as startpoint of the development of the theory of B-splines, rather than using divided differences.
Theorem 10 (Curry, Schoenberg (1966), de Boor, Fix (1973)) Given a < b, r > 0, basic knots
t = {a < t1 < < tn < b} and 2r auxiliary knots {t1-r <
< tn < b} and 2r auxiliary knots {t1-r < < t0 < a}, {b < tn+1 <
< t0 < a}, {b < tn+1 < < tn+r}, the
puB-splines Nk,r(x) = N(x|tk,...,tk+r) for k = 1 - r,...,n form a basis of Sr(t;[a,b]).
< tn+r}, the
puB-splines Nk,r(x) = N(x|tk,...,tk+r) for k = 1 - r,...,n form a basis of Sr(t;[a,b]).
Proof. Although the result was first proved by Curry and Schoenberg [CuSc] in 1966, we will offer here a different
proof by de Boor and Fix [dBFi], based on the Marsden identities:
-
- Step 1. The restriction to the interval [a,b] of the previously defined puB-splines Nk,r(x) gives a partition
of unity:
![n
sum Nk,r(x)| [a,b] = x
k=1- r [a,b]](root107x.gif) This is a direct consequence of the recurrence formula for puB-splines. We can therefore use induction on r, since for r = 1 we have trivially:
This is a direct consequence of the recurrence formula for puB-splines. We can therefore use induction on r, since for r = 1 we have trivially:
![n n
sum Nk,1| [a,b] = sum x = x
k=0 k=0 [tk,tk+1) /~\ [a,b] [a,b]](root109x.gif)
-
- Step 2. Marsden identities: For any


 ,
,
![n
--1---(q- x)r-1| = sum g (q)N (x)| ,
(r - 1)! [a,b] k=1- r k,r k,r [a,b]](root110x.gif) where for all k = 1 - r,...,n, We will prove this statement by induction on r: It has been proved true for r = 1 above. Assume the property
holds up to r - 1; then, Let us rewrite the coefficients of each puB-spline in the previous expression: therefore,
where for all k = 1 - r,...,n, We will prove this statement by induction on r: It has been proved true for r = 1 above. Assume the property
holds up to r - 1; then, Let us rewrite the coefficients of each puB-spline in the previous expression: therefore,
![n sum q---x sum n (q--x)r-1
gk,r(q)Nk,r(x)|[a,b] = r- 1 gk,r- 1(q)Nk,r- 1(x)| [a,b] = (r- 1)!
k=1- r k=2-r](root114x.gif)
-
- Step 3. puB-spline series of polynomials in
 (r): For any
(r): For any 

 , and any polynomial P
, and any polynomial P 
 (r), we can
write
(r), we can
write
![n sum r sum -1
P = gk,r(P )Nk,r| [a,b], where gk,r(P) = (-1)ng(r- n- 1)(q)P (n)(q).
k=1- r n=0 k,r](root115x.gif) The functionals
The functionals  k,r are called de Boor-Fix functionals.
k,r are called de Boor-Fix functionals.
Notice first that the previous Marsden’s identities can be completed with the expression of any power ( -x)
-x) for
for  < r - 1 by differentiation:
< r - 1 by differentiation:
Given now any polynomial P 
 (r), consider any value
(r), consider any value 

 and the Taylor expansion of P around
and the Taylor expansion of P around
 :
:
![r sum -1 (x- q)n r sum -1 sum n (r-n-1)
P (x) = P(n)(q)---n!-- = (- 1)nP (n)(q) gk,r (q)Nk,r(x)| [a,b],
n=0 n=0 k=1- r](root117x.gif) which, after rearrangement, gives the desired coefficients.
which, after rearrangement, gives the desired coefficients.
It only remains to prove that a different choice of 

 leads to the same coefficients, and therefore the
functionals
leads to the same coefficients, and therefore the
functionals  k,r :
k,r :  (r)
(r) 
 do not depend on this choice; let
do not depend on this choice; let  '
'
 , and write each derivative P(
, and write each derivative P( ) in Taylor
expansion around
) in Taylor
expansion around  ':
':
 Notice that then,
Notice that then,
-
- Step 4. puB-spline series of truncated powers: For any basic knot tj and a power
 for 0 <
for 0 <  < r -mj (being mj
the multiplicity of the knot tj),
< r -mj (being mj
the multiplicity of the knot tj),
![n n sum
(x--tj)+-= (- 1)n g(rk,-rn-1)(tj)Nk,r(x)| [a,b].
n! k=j](root121x.gif) This is a direct consequence of the previous step; for any basic knot tj, it must be 1 < j < n, and we can write:
as we wanted to prove.
This is a direct consequence of the previous step; for any basic knot tj, it must be 1 < j < n, and we can write:
as we wanted to prove.
Conclusion: We have expressions of every basic element of Sr(t;[a,b]) in terms of the constructed puB-splines. This
means that they span the Schoenberg space, and because of their cardinality, they must form a basis of the space.
![[#]](msam10-4.gif)
Remark. Consider the dual functionals associated to the basis of Sr(t;[a,b]) given by the puB-splines; let us denote
them  k,r. There are different ways of expressing these functionals; de Boor and Fix offer the most
useful for our purposes: For each k = 1 - r,...,n, choose
k,r. There are different ways of expressing these functionals; de Boor and Fix offer the most
useful for our purposes: For each k = 1 - r,...,n, choose  k,r
k,r  supp(Nk,r) = (tk,tk+r)
supp(Nk,r) = (tk,tk+r)  [a,b], and
write
[a,b], and
write
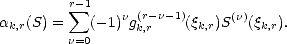 The
convenction is that, if
The
convenction is that, if  k,r is one of the knots, then some of the terms in the sum are zero, those where gk,r
vanishes.
k,r is one of the knots, then some of the terms in the sum are zero, those where gk,r
vanishes.
Consider the functional Qt : Sr(t,[a,b]) 
 given by
given by
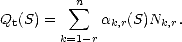 One
may try to extend this functional to the whole space X; for this task it sometimes suffices to use the Hahn Banach
Lemma (Theorem 28 in page 101), although in most of the cases, the hypothesis of this Theorem are not satisfied,
and one must look for other related constructions and partial extensions into proper subspaces of X. We will get
back to this idea in §2.5.
One
may try to extend this functional to the whole space X; for this task it sometimes suffices to use the Hahn Banach
Lemma (Theorem 28 in page 101), although in most of the cases, the hypothesis of this Theorem are not satisfied,
and one must look for other related constructions and partial extensions into proper subspaces of X. We will get
back to this idea in §2.5.
2.4.2 Quasi-Interpolant Operators
It is not hard to show that the projector Qt is a bounded operator on the Schoenberg spaces; given S  Sr(t;[a,b]),
we have
Sr(t;[a,b]),
we have
Notice that the bound depends on the number of knots, n, and this is not useful in the sense that, when the number
of knots gets bigger the constant may grown closer and closer to infinity. But there are good news; one can use the
scaling properties of our puB-splines to find a bound independent of the number of knots. In order to achieve this
surprising result, we must consider a special choice of subintervals associated to each puB-spline function: For each
puB-spline Nk,r, we will denote Jk,r the largest subinterval (tj,tj+1) on its support (in case of several
subintervals with the same property, choose the one with smallest index j). Notice that it must be
|Jk,r|> (tj+r - tj)/r. Also, for each subinterval (tj,tj+1), we will consider the slightly larger subinterval
(tj-r+1,tj+r)  [a,b], which we denote Ij,r. Notice that Jk,r
[a,b], which we denote Ij,r. Notice that Jk,r  Ij,r whenever the interval (tj,tj+1) is
contained in the support of the puB-spline Nk,r, and that the number of intervals Jk,r contained on each
Ij,r is preciselly r (this will be used several times to achieve dependence of r on several constants).
Ij,r whenever the interval (tj,tj+1) is
contained in the support of the puB-spline Nk,r, and that the number of intervals Jk,r contained on each
Ij,r is preciselly r (this will be used several times to achieve dependence of r on several constants).
Proof. We will use Lemma 2.1 (page 30), Markov’s Theorem (page 33), and the fact that the functions gk,r and
their derivatives are polynomials, hence bounded in any compact. Consider any point  k,r
k,r  Jk,r:
Jk,r:
Remark. For p > 1, using the Hahn-Banach Theorem (Theorem 29 in page 102), we realize that we can extend
these functionals to Lp[a,b]: For each k there exists a linear functional (abusing notation, we denote them equally)
such that 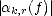 < C|Jk,r|-1/p||f||Lp(Jk,r) for all f
< C|Jk,r|-1/p||f||Lp(Jk,r) for all f  Lp(Jk,r). Furthermore, we can also extend the linear
operator Qt to Lp[a,b] for p > 1. This is what we call the quasi-interpolant of order r corresponding to the knots t in
[a,b].
Lp(Jk,r). Furthermore, we can also extend the linear
operator Qt to Lp[a,b] for p > 1. This is what we call the quasi-interpolant of order r corresponding to the knots t in
[a,b].
Proposition 5 For all 1 < p < , and all f
, and all f  Lp[a,b], there exists a constant C > 0 that depends at most on p
and the order r, such that the following local and global estimates hold:
Lp[a,b], there exists a constant C > 0 that depends at most on p
and the order r, such that the following local and global estimates hold:
Proof. Estimate (2.3) is a direct consecuence of the remark after Lemma 2.9, the “partition of unity” property
of the puB-splines, and the fact that |Jk,r|> (tk+r - tk)/r and Jk,r  Ij,r for all suitable index j:
Ij,r for all suitable index j:
And the first estimate follows. Estimate (2.4) is a direct consequence of the previous:
Remark. Unfortunatelly, one cannot use Hahn-Banach to find the same kind of results for 0 < p < 1,
although similar approximation results will remain valid. In §2.5 we will show how in a more general
setup.
2.5 Tensor Product Splines: Description of the problem
We have all the necessary ingredients to pose the problem of approximation on cubes of  d by dyadic splines. Let
d by dyadic splines. Let
 = [0,1]d be the unit cube in
= [0,1]d be the unit cube in  d, and let X = Lp(
d, and let X = Lp( ) with the corresponding (quasi)norm for all 0 < p <
) with the corresponding (quasi)norm for all 0 < p < . The
family of approximants will be constructed as spaces spanned by tensor product puB-splines. The construction of
those spaces starts in the real line:
. The
family of approximants will be constructed as spaces spanned by tensor product puB-splines. The construction of
those spaces starts in the real line:
Consider for each n 
 the basic knots in [0,1]
the basic knots in [0,1] 
 given by tn = {k2-n : 0 < k < 2n}, and t0 = Ø by definition.
Associated to these basic knots we will use the following Schoenberg spaces:
given by tn = {k2-n : 0 < k < 2n}, and t0 = Ø by definition.
Associated to these basic knots we will use the following Schoenberg spaces:
-
n = 0 :
- Consider auxiliary knots 1 - r,...,0 and 1,...,r, and the corresponding puB-splines Nk,r = N(. |
k,...,k + r) for all k = 1 - r,...,0. Notice that all of those functions may be obtained as (restrictions
on [0,1] of) horizontal shifts of N0,r. We can then write Nk,r(x) = N0,r(x - k).
-
n > 1 :
- Consider auxiliary knots k2-n for k = 1 - r,...,0 and k = 2n,...,2n + r - 1, and the corresponding
puB-splines. Notice that, as in the previous case, we can obtain each of them as (restrictions on [0,1]
of) horizontal shifts of dyadic dilations of N0,r. We need to update our notation in order to handle the
new situation:
For each n > 0, denote N0,r[n](x) = N0,r(2nx) (the dyadic dilation of order 2-n), and then for each
k = 1 - r,...,2n - r - 1, Nk,r[n](x) = N0,r(2nx - k) (horizontal left-shifts of length k2-n).
Notice that {Nk,r[n]}k=1-r2n-1
is a basis for Sr(tn,[0,1]); let us denote  k,r[n] the corresponding dual
functionals.
k,r[n] the corresponding dual
functionals.
Let us move into d dimensions, where we will write x = (x1,...,xd) 
 d. Consider for each multi-index
k = (k1,...,kd), the tensor product puB-spline Nk,r[n](x) = Nk1,r[n](x1)
d. Consider for each multi-index
k = (k1,...,kd), the tensor product puB-spline Nk,r[n](x) = Nk1,r[n](x1) Nkd,r[n](xd), and the functionals
Nkd,r[n](xd), and the functionals
 k,r[n] =
k,r[n] =  k1,r[n] o
k1,r[n] o o
o  kd,r[n].
kd,r[n].
Lemma 2.10 For each S  Xn, any tensor product puB-spline Nk,r[n] = Nk1,r
Xn, any tensor product puB-spline Nk,r[n] = Nk1,r Nkd,r, and any point
Nkd,r, and any point
 k,r = (
k,r = ( k1,r,...,
k1,r,..., kd,r)
kd,r)  supp(Nk,r[n])
supp(Nk,r[n]) 
 , (
, ( kj,r
kj,r  supp(Nkj,r)
supp(Nkj,r)  projj(
projj( )),
)),
 = sum a (q )DnS(q ), where a (q ) = (-1)|n|g(r-n1-1)(q )...g(r-nd- 1)(q ).
k,r n=0 n,k,r k,r k,r n,k,r k,r k1,r k1,r kd,r kd,r](root136x.gif)
Proof. Given a multi-index k = (k1,...,kd), and a tensor product spline S  Xn, write
Xn, write
![sum sum
S = cjN [nj,]r + Nkd,r cj'N[jn',]r.
jd/=kd j' (- Zd- 1](root137x.gif) Make
Make
 kd,r act on the previous expression to obtain
kd,r act on the previous expression to obtain
![r sum -1 ( sum )
akd,r(S) = (-1)n1g(r-n1-1)(qkd,r) cj'N[n'] Dn1Nkd,r(qkd,r).
n1=0 kd,r j' (- Zd-1 j,r](root138x.gif) Make
now the rest of the univariate functionals
Make
now the rest of the univariate functionals  kj,r act on the previous expression, one at a time in decreasing order, to
obtain the desired result.
kj,r act on the previous expression, one at a time in decreasing order, to
obtain the desired result. ![[#]](msam10-4.gif)
It follows that these are the dual functionals of the constructed tensor product puB-splines, and therefore the
functions Nk,r[n] are linearly independent in Lp( ). Let us denote Xn = span{Nk,r[n]}, where k has all its indices
between 1 - r and 2n - 1. This is the space of all piecewise polynomials with coordinate order r and
maximal smoothness on dyadic subcubes of size 2-n in the cube
). Let us denote Xn = span{Nk,r[n]}, where k has all its indices
between 1 - r and 2n - 1. This is the space of all piecewise polynomials with coordinate order r and
maximal smoothness on dyadic subcubes of size 2-n in the cube  (since D
(since D Nk,r[n]
Nk,r[n]  L
L (
( ) for all
multi-index 0 <
) for all
multi-index 0 <  < r - 1, and D
< r - 1, and D Nk,r[n] is continuous for multi-indices 0 <
Nk,r[n] is continuous for multi-indices 0 <  < r - 2). As in the
univariate case, each tensor product puB-spline Nk,r[n] can be obtained from N0,r[0] by shifts and
dilations:
< r - 2). As in the
univariate case, each tensor product puB-spline Nk,r[n] can be obtained from N0,r[0] by shifts and
dilations:
![[n] [0] n
N k,r(x) = N 0,r(2x - k)](root139x.gif)
The family {Xn}n is our family of approximants:
- Each Xn is a linear space:
 Xn = Xn, and Xn + Xn = Xn trivially.
Xn = Xn, and Xn + Xn = Xn trivially.
- By Theorem 3 (page 14), there exist elements of best approximation, although so far we have no means
of computing them for a given f
 Lp(
Lp( ). By using the construction below and the results in sections
2.1, 2.4.2, we will be nevertheless able to construct suitable elements of near-best approximation.
). By using the construction below and the results in sections
2.1, 2.4.2, we will be nevertheless able to construct suitable elements of near-best approximation.
- Notice that Xn+1
 Xn for all n. It can be proved that
Xn for all n. It can be proved that  nXn is dense in X, and therefore
limnE(.,Xn) = 0 monotonically decreasing. We can therefore use Lemma 1.1 (page 5) if needed.
nXn is dense in X, and therefore
limnE(.,Xn) = 0 monotonically decreasing. We can therefore use Lemma 1.1 (page 5) if needed.
We would like now to have a projector, but this is not an easy task. The quasi-interpolant of §2.4.2 does not work
for 0 < p < 1, but is still useful. The trick is to find first intermediate spaces Xn  Y n
Y n  X for each n, where
the quasi-interpolants can be easily extended, and such that we can effectively compute (near)best
approximations from Y n to elements of X. In the case we are studying here, the obvious choice works just
fine:
X for each n, where
the quasi-interpolants can be easily extended, and such that we can effectively compute (near)best
approximations from Y n to elements of X. In the case we are studying here, the obvious choice works just
fine:
For each multi-index j = (j1,...,jd) with 1 < ji < 2n, consider the dyadic cubes of  ,
,
![[]](msam10-3.gif) j,n = [(j1 - 1)2-n,j12-n] ×
j,n = [(j1 - 1)2-n,j12-n] × × [(jd - 1)2-n,jd2-n], and Dn = {
× [(jd - 1)2-n,jd2-n], and Dn = {![[]](msam10-3.gif) j,r : 1 < j < 2n} the family of those cubes. Let
us denote Y n =
j,r : 1 < j < 2n} the family of those cubes. Let
us denote Y n = 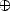 j=12n
j=12n
 (r;
(r;![[]](msam10-3.gif) j,n) the space of piecewise polynomials of coordinate order r associated to the dyadic
partition Dn.
j,n) the space of piecewise polynomials of coordinate order r associated to the dyadic
partition Dn.
As we did before for univariate puB-splines, we need to consider for each tensor product puB-spline Nk,r[n], two
especial cubes:
-
Jk,r:
- Jk,r = Jk1,r ×
 × Jkd,r
× Jkd,r  Dn (read §2.4.2 for the definition of the intervals Jj).
Dn (read §2.4.2 for the definition of the intervals Jj).
-
Ij,r:
- For each 1 < j < 2n, denote Ij,r the smallest cube that contains each of the Jk,r for which supp(Nk,r[n])

![[]](msam10-3.gif) j,n
j,n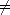 Ø. Notice that Ij,r
Ø. Notice that Ij,r  Dm for some m < n; therefore,
Dm for some m < n; therefore, 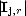 = 2(n-m)d
= 2(n-m)d![|[]j,n|](root144x.gif) . Also, and as before,
the number of subcubes Jj,r contained on each Ik,r depends solely on r and d.
. Also, and as before,
the number of subcubes Jj,r contained on each Ik,r depends solely on r and d.
In order to obtain the de Boor-Fix expression of the dual functionals of the tensor product puB-splines Nk,r[n], we
will choose canonically  k,r to be the center of the cubes Jk,r. In that case, one realizes that these functionals can
also be applied to any function f
k,r to be the center of the cubes Jk,r. In that case, one realizes that these functionals can
also be applied to any function f  Lp(
Lp( ) which is differentiable enough on each of the points
) which is differentiable enough on each of the points  k,r; in particular,
any piecewise polynomial P
k,r; in particular,
any piecewise polynomial P  Y n:
Y n:
The proof of this lemma follows the same steps that the one for Lemma 2.9 (page 47) and its posterior remark.
We can also construct quasi-interpolant operators Qn : Y n  Xn, which act naturally as projectors.
Xn, which act naturally as projectors.
The proof is trivial; it uses the previous lemma, and follows the same steps that the proof of Proposition 5 and its
posterior remark (page 48).
We are ready to construct the method of approximation: Given  > 0, consider any operator of
> 0, consider any operator of  near-best Lp
approximation by elements of Y n, say
near-best Lp
approximation by elements of Y n, say  n : X
n : X  Y n such that
Y n such that 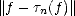 Lp(
Lp( ) <
) <  E(f,Y n)p. Notice
that such operators may be constructed by collecting the restriction on cubes of the
E(f,Y n)p. Notice
that such operators may be constructed by collecting the restriction on cubes of the  near-best Lp
approximations to f by polynomials in
near-best Lp
approximations to f by polynomials in  (r) on each cube
(r) on each cube ![[]](msam10-3.gif) j,n
j,n  Dn, and patching them together. Let
then
Dn, and patching them together. Let
then
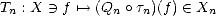 It
follows easily that these are linear operators. The most important properties of these operators are presented in the
following two propositions:
It
follows easily that these are linear operators. The most important properties of these operators are presented in the
following two propositions:
Proof. Notice first that, for all subcube ![[]](msam10-3.gif) j,n
j,n  Dn, we have
Dn, we have
therefore,
Proposition 8 Tn : Lp( )
)  Xn is an operator of near-best Lp approximation from elements of Xn.
Xn is an operator of near-best Lp approximation from elements of Xn.
Proof. Given f  Lp(
Lp( ), let Sn
), let Sn  Xn be its best Lp approximation from Xn; then, we have the estimate:
Xn be its best Lp approximation from Xn; then, we have the estimate:
which proves the statement. ![[#]](msam10-4.gif)
Remark. Notice that now we may use indisctinctly for each f  Lp(
Lp( ) either E(f,Xn)p or ||f -Tn(f)||LP(
) either E(f,Xn)p or ||f -Tn(f)||LP( ), since
they are equivalent. Moreover, when searching for the approximation spaces, we may use the (quasi)seminorm
functions
), since
they are equivalent. Moreover, when searching for the approximation spaces, we may use the (quasi)seminorm
functions
Our next goal is to try to identify the approximation spaces Aq (Lp(
(Lp( ),Xn) in terms of classical spaces. For
this task, the first step to take is to find known (quasi)seminorms with the same properties than our
objects ||f - Tn(f)||Lp(
),Xn) in terms of classical spaces. For
this task, the first step to take is to find known (quasi)seminorms with the same properties than our
objects ||f - Tn(f)||Lp( ). Among the properties we are interested, the most obvious is that the space of
polynomials of coordinate order r is properly contained on each of the kernels. Good candidates are
therefore the Sobolev seminorms (but these are only defined for values p > 1 and even in those cases, not
for all functions in Lp(
). Among the properties we are interested, the most obvious is that the space of
polynomials of coordinate order r is properly contained on each of the kernels. Good candidates are
therefore the Sobolev seminorms (but these are only defined for values p > 1 and even in those cases, not
for all functions in Lp( )), and the r-th moduli of smoothness (and these do exist for all functions
f
)), and the r-th moduli of smoothness (and these do exist for all functions
f  Lp(
Lp( ), 0 < p <
), 0 < p < ). We will explore both functionals and the spaces related to them in the next
sections.
). We will explore both functionals and the spaces related to them in the next
sections.
2.6 Sobolev Spaces
2.6.1 Mollifiers and Infinitelly Differentiable Partitions of Unity
In this section we introduce two important tools in the Theory of Sobolev Spaces: mollifiers and infinite
differentiable partitions of unity. We also illustrate how to use the former to construct plateau functions and prove
the density of C0 (G) on Lp(G) for 1 < p <
(G) on Lp(G) for 1 < p <  on domains G
on domains G 
 d.
d.
Example. An example of mollifying kernels are the “bump” functions 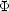 d :
d :  d
d 
 given by
given by
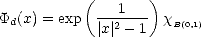
Proof. Assume f  M(
M( d,|.|). Let (sn)n be a monotonically increasing sequence of nonnegative simple
functions converging pointwise to f. As p > 1, we have 0 < sn(x)p < f(x)p a.e., and therefore, it must
be sn
d,|.|). Let (sn)n be a monotonically increasing sequence of nonnegative simple
functions converging pointwise to f. As p > 1, we have 0 < sn(x)p < f(x)p a.e., and therefore, it must
be sn  Lp(G), and furthermore, by the Dominated convergence Theorem, limn||f - sn||Lp(G) = 0
(since |f(x) - sn(x)|p < f(x)p for all x). Given
Lp(G), and furthermore, by the Dominated convergence Theorem, limn||f - sn||Lp(G) = 0
(since |f(x) - sn(x)|p < f(x)p for all x). Given  > 0, find sn such that ||f - sn||Lp(G) <
> 0, find sn such that ||f - sn||Lp(G) <  /2. Use
now Lusin’s Theorem to find a continuous function g
/2. Use
now Lusin’s Theorem to find a continuous function g  C(G) such that |g(x)|<||sn||L
C(G) such that |g(x)|<||sn||L (G) and more
importantly,
(G) and more
importantly,
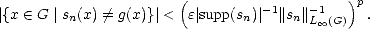 We
have then
We
have then
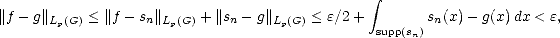 and
the result follows.
and
the result follows. ![[#]](msam10-4.gif)
Lemma 2.12 Given a domain G 
 d, a mollification kernel
d, a mollification kernel 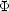 and a function f
and a function f  M(
M( d,|.|) such that
f(x) = 0 for x /
d,|.|) such that
f(x) = 0 for x / G, the following holds:
(i) If f
G, the following holds:
(i) If f  L1loc(G), then
L1loc(G), then 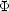
 * f
* f  C
C (
( d) for all
d) for all  > 0.
(ii) If also supp(f) is compact, then
> 0.
(ii) If also supp(f) is compact, then 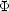
 * f
* f  C0
C0 (G) for all 0 <
(G) for all 0 <  < dist(supp(f),
< dist(supp(f), G).
(iii) If f
G).
(iii) If f  Lp(G) for any 1 < p <
Lp(G) for any 1 < p <  , then
, then 
 * f
* f  Lp(G); moreover,
Lp(G); moreover,
 (iv) If f
(iv) If f  C
C(
G)
and K  G is compact, then
G is compact, then lim

 0+
0+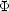
 * f
* f =
f uniformly on K.
(v) If f  C
C(
G)
, then lim

 0+
0+
 * f
* f =
f uniformly on G.
Theorem 12 Given a domain G 
 d, a compact subset K
d, a compact subset K  G and
G and 0
< 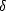 <
< dist(
K,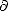 G
G)
, there is a plateau
function 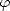

 C0
C0
(
G)
such that 0
< 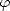

(
x)
< 1
for all x  G, and
G, and 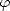

(
x) = 1
for all x  K
K
=
 y
y KB
KB(
y,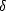
)
.
Proof. Let 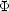 :
:  d
d 
 be a mollifying kernel, and consider
be a mollifying kernel, and consider 
 =
= 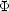
 *
*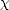 K
3
K
3 /2, the mollification of
/2, the mollification of 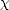 K3
K3 /2 with
/2 with  . This
is the function we are looking for.
. This
is the function we are looking for. ![[#]](msam10-4.gif)
Proof. This is a direct consequence of Theorem 11 and parts (ii) and (v) of the previous Lemma. ![[#]](msam10-4.gif)
2.6.2 Distributions and Weak Derivatives
Remark. The space L1loc(G) can be identified with a subspace of D'(G) as follows: given f  L1loc(G), let
Tf : C0
L1loc(G), let
Tf : C0 (G)
(G)  g
g
 Gf(x)g(x)dx
Gf(x)g(x)dx 
 . These functionals are trivially linear. Notice that it is also continuous:
Given a sequence (gn)n in C0
. These functionals are trivially linear. Notice that it is also continuous:
Given a sequence (gn)n in C0 (G) such that there exists a compact K
(G) such that there exists a compact K  G so that supp(g -gn)
G so that supp(g -gn)  K for all n, and
limngn(x) = g(x) uniformly on K; we have
K for all n, and
limngn(x) = g(x) uniformly on K; we have
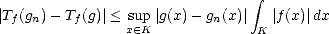 and
the continuity holds in virtue of the uniform convergence of (gn)n. The identification is possible via Theorem 13: If
Tf1 = Tf2, then
and
the continuity holds in virtue of the uniform convergence of (gn)n. The identification is possible via Theorem 13: If
Tf1 = Tf2, then  G(f1 -f2)g dx = 0 for all g
G(f1 -f2)g dx = 0 for all g  C0
C0 ; the density gives
; the density gives 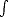 G(f1 -f2)g dx = 0 for all g
G(f1 -f2)g dx = 0 for all g  Lp(G), and
therefore, f1 -f2 = 0 a.e. This means that the map L1loc(G)
Lp(G), and
therefore, f1 -f2 = 0 a.e. This means that the map L1loc(G)  D'(G) that gives the identification is an injection.
D'(G) that gives the identification is an injection.
2.6.3 Sobolev Spaces Wpr(G) and Hpr(G)
Remark. We have trivially Wp0(G) = Lp(G) for 1 < p < , and Wp0(G) = Lp(G) for 1 < p <
, and Wp0(G) = Lp(G) for 1 < p <  (by Theorem
13). Notice also the chain of (continuous) embeddings for all r
(by Theorem
13). Notice also the chain of (continuous) embeddings for all r 
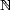 :
:
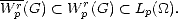 We
will prove that Hpr(G) = Wpr(G) for 1 < p <
We
will prove that Hpr(G) = Wpr(G) for 1 < p <  , and H
, and H r(G)
r(G) 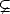 W
W r(G)
r(G)
Proof. Let (fn)n be a Cauchy sequence in Wpr(G)  Lp; then trivially (Dkfn)n are Cauchy sequences in Lp(G) for
all multi-index k with 0 <|k|< r. Let f,
Lp; then trivially (Dkfn)n are Cauchy sequences in Lp(G) for
all multi-index k with 0 <|k|< r. Let f,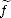 (k)
(k)  Lp(G) be such that limnfn = f and limnDkf =
Lp(G) be such that limnfn = f and limnDkf = 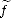 (k) both in Lp(G).
As Lp(G)
(k) both in Lp(G).
As Lp(G)  L1loc(G), each of those functions determines distributions Tf,T
L1loc(G), each of those functions determines distributions Tf,T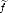 (k)
(k)  D'(G). For any g
D'(G). For any g  D(G), we
have then (let q be the conjugate exponent of p):
D(G), we
have then (let q be the conjugate exponent of p):
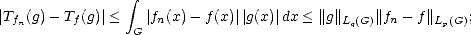 therefore, limnTfn(g) = Tf(g) and similarly, limnTDkfn(g) = T
therefore, limnTfn(g) = Tf(g) and similarly, limnTDkfn(g) = T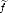 (k)(g) for all g
(k)(g) for all g  D(G). It follows
that
D(G). It follows
that
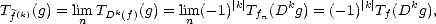 and
hence
and
hence 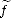 (k) = Dkf in the distributional sense. The statement follows.
(k) = Dkf in the distributional sense. The statement follows. ![[#]](msam10-4.gif)
Theorem 16 (Meyers, Serrin) Given a domain G 
 d,
d, 1
< p <  , and r
, and r 
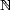
 {
{0
}, we have
Hpr(
G) =
Wpr(
G)
.
2.6.4 Properties of Sobolev Spaces in one dimension
For functions of one variable, both ordinary and generalized derivatives produce the dame space. This is proved in
the following two results:
Proposition 9 If f  L1loc
L1loc(
A)
has a weak r-th derivative 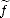 (r)
(r)  L1loc
L1loc(
A)
, then it can be redefined on a set
of measure zero so that f(r-1) is absolutelly continuous, and f(r) =
ga.e. on A.
Remark. In §2.7.2 we will make use of the K-functional of compatible couples (Lp(G),Wpr(G)) for G 
 d. We
can use the previous results to illustrate how to compute it in one dimension. We will base the proof in the
availability of the Taylor polynomial for functions in Sobolev Spaces: For each f
d. We
can use the previous results to illustrate how to compute it in one dimension. We will base the proof in the
availability of the Taylor polynomial for functions in Sobolev Spaces: For each f  Wpr(A), consider the Taylor
polynomial centered in c
Wpr(A), consider the Taylor
polynomial centered in c  A:
A:
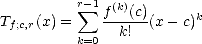 with
error
with
error
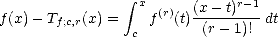
Proof. Let p' be the conjugate exponent of p; let’s apply Hölder’s Inequality:
therefore, for each 1 < q < , hence proving the desired statement.
, hence proving the desired statement. ![[#]](msam10-4.gif)
Theorem 17 For r > 2
, 1
< p < , there is a constant C >
, there is a constant C > 0
depending at most on r, such that for all
f  Wpr
Wpr(
A)
, 0
< t >|A| and 0
< k < r,
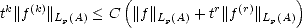
Proof. Given 0 < t <|A|, we have for all x  At = {x
At = {x  A | x + t
A | x + t  A},
A},
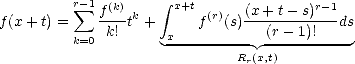 Notice
that and therefore,
Notice
that and therefore,
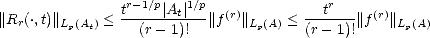 | (2.12) |
since |At|< t trivially.
Consider now for our choice of 0 < t < |A|, x  A and
A and  > 0 such that x +
> 0 such that x +  t
t  A. In this case, we
have
A. In this case, we
have
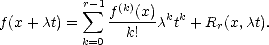 Choose
Choose  > 1 small, and r - 1 different values 1 <
> 1 small, and r - 1 different values 1 <  1 <
1 < <
<  r-1 <
r-1 <  . Construct the following system of linear
equations:
. Construct the following system of linear
equations:
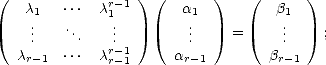 where
where
 k = tkf(k)(x)/k!, and
k = tkf(k)(x)/k!, and 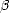 k = f(x +
k = f(x +  kt) -f(x) -Rr(x,
kt) -f(x) -Rr(x, kt). The first matrix is a Vandermonde’s; hence this system
has a solution:
kt). The first matrix is a Vandermonde’s; hence this system
has a solution:
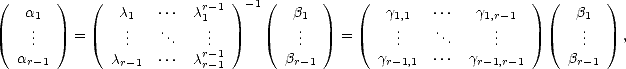 where
the values
where
the values 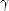 i,j are controled by the values
i,j are controled by the values  k. We have then
k. We have then  k =
k = 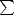 j=1r-1
j=1r-1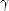 kj
kj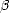 j for all j = 1,...,r - 1.
j for all j = 1,...,r - 1.
This leads to and the statement follows.
2.7 Modulus of smoothness and Besov Spaces
2.7.1 Definitions and Properties
Consider the difference operators: for each h 
 d and measurable function f
d and measurable function f  M(
M( ,|.|) for any subset
,|.|) for any subset 

 d, let
d, let
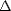 h(f,.) = f(. + h) - f(.), and
h(f,.) = f(. + h) - f(.), and 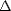 hr =
hr =  h(
h(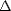 hr-1) for r > 1. It follows from the binomial theorem,
that
hr-1) for r > 1. It follows from the binomial theorem,
that
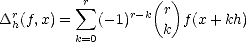 | (2.13) |
for all x 
 (rh) = {x
(rh) = {x 
 ||x + kh|
||x + kh|
 for all 1 < k < r}.
for all 1 < k < r}.
The general setup is fairly complicated, and many different properties are to be taken into account in
order to produce any general result on these functionals. We will focus on the spaces we are going to
use in this survey: Lp( ) for 0 < p <
) for 0 < p <  , and C(
, and C( ) for p =
) for p =  , where
, where 

 d is a compact cube.
d is a compact cube.
Lemma 2.16 For any t > 0, the modulus of smoothness is a seminorm for 1 < p < and a quasi-seminorm
for 0 < p < 1.
and a quasi-seminorm
for 0 < p < 1.
Proof. Notice that  r(
r( f,t)p <|
f,t)p <| |
| r(f,t)p, and
r(f,t)p, and  r(0,t)p = 0 trivially for all 0 < p <
r(0,t)p = 0 trivially for all 0 < p < . As for the (quasi)triangular
inequality, we have also trivially
. As for the (quasi)triangular
inequality, we have also trivially  r(f + g,t)p < C
r(f + g,t)p < C , with the same constant from the
(quasi)triangular inequality in Lp(
, with the same constant from the
(quasi)triangular inequality in Lp( (rh)). The kernel of the r-th modulus of smoothness is precisely the set of
polynomials
(rh)). The kernel of the r-th modulus of smoothness is precisely the set of
polynomials  (r) of coordinate order r.
(r) of coordinate order r.
Also, from the fact that ||f + g||Lpp <||f||Lpp + ||g||Lpp for all 0 < p < 1, we obtain similarly
 r(f + g,t)pp <
r(f + g,t)pp <  r(f,t)pp +
r(f,t)pp +  r(g,t)pp.
r(g,t)pp. ![[#]](msam10-4.gif)
Lemma 2.17 (Properties of the modulus of smoothness in Lp) Given f  Lp(
Lp( ), t > 0, the following
estimates hold:
), t > 0, the following
estimates hold:
Proof. The first estimate can be proved directly from the identity 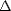 hr(f,x) =
hr(f,x) = 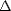 hr-1(f,x) +
hr-1(f,x) + 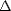 hr-1(f,x + h), which
is proved easily from (2.13). That gives
hr-1(f,x + h), which
is proved easily from (2.13). That gives  r(f,t)pmin(1,p) < 2
r(f,t)pmin(1,p) < 2 r-1(f,t)pmin(1,p), and from this the statement
follows.
r-1(f,t)pmin(1,p), and from this the statement
follows.
As for the second estimate, notice first that
 We
use next the following expansion for
We
use next the following expansion for 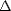 nhr:
nhr:
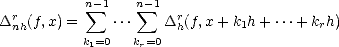 And
the third estimate is a direct consequence of the second.
And
the third estimate is a direct consequence of the second. ![[#]](msam10-4.gif)
Weak inverses to the first estimate in the previous lemma are offered by Marchaud and Timan. A proof of
the following result, that is known as Marchaud’s Inequalities, can be read in chapter 2 of [DeLo].
Theorem 18 (Marchaud (1927),Timan (1958)) Given r > 2 and f  Lp(
Lp( ), we have the following estimates
for all 1 < k < r, t > 0 and 0 < p <
), we have the following estimates
for all 1 < k < r, t > 0 and 0 < p < :
:
And for 1
< p <  ,
, 
= min(
p,2)
: ![[]](msam10-3.gif)
Lemma 2.18 If  is compact, then the previous (quasi)seminorms are equivalent to their discrete counterparts:
is compact, then the previous (quasi)seminorms are equivalent to their discrete counterparts:
Sketch of the Proof. The proof is similar to the proof of part (ii) in Lemma 1.9 (page 21): we start showing that the
seminorm above is equivalent to the one obtained replacing the integral (or the supremum) over (0, ) by one over
(0,1), using the fact that, as
) by one over
(0,1), using the fact that, as  is compact, then
is compact, then  r(f,t)p <
r(f,t)p <  r(f,|
r(f,| |)p for all t > |
|)p for all t > | |. After that, discretization of
the latter integral with partition {2-n | n
|. After that, discretization of
the latter integral with partition {2-n | n 
 } is applied, using the fact that
} is applied, using the fact that  r(f,.)p is a nondecreasing function.
r(f,.)p is a nondecreasing function.
![[]](msam10-3.gif) .
.
Remark. Unfortunately, the moduli of smoothness are not always suitable for applications because it is not easy to
add up several such estimates over different intervals. New related (and equivalent) moduli of smoothness can be
constructed by averaging:
Remark. Notice that, for I,J 
 , we have (I
, we have (I  J)(h)
J)(h)  I(h)
I(h)  J(h) for all suitable h
J(h) for all suitable h 
 d; therefore,
wr(f,t;I
d; therefore,
wr(f,t;I  J)pp > wr(f,t;I)pp + wr(f,t;J)pp. We will prove now the equivalence with the moduli of smoothness.
J)pp > wr(f,t;I)pp + wr(f,t;J)pp. We will prove now the equivalence with the moduli of smoothness.
Proof. Notice that
therefore,
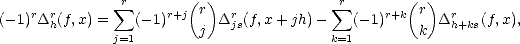 and
the statement follows.
and
the statement follows. ![[#]](msam10-4.gif)
Proposition 10 For all f  Lp
Lp(

)
, a subcube I 
 , r >
, r > 0
and any 0
< t < |I|(4
r)
-1, there exists a
constant C > 0
which depends at most on r such that
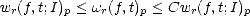
Proof. The left inequality is trivial:
![integral
p -d r p p
wr(f,t;I)p = t [-t,t]d||D h(f,.)||Lp(I(rh))dh < wr(f,t)p](root205x.gif) Blah
blah blah.
Blah
blah blah. ![[]](msam10-3.gif) Remark. We will prove that the Besov spaces are precisely the ones we are looking for. The key is Whitney’s
theorem.
Remark. We will prove that the Besov spaces are precisely the ones we are looking for. The key is Whitney’s
theorem.
2.7.2 Whitney’s Theorem
Proof. Oh boy, this is a tough one. ![[]](msam10-3.gif)
Proof. For p > 1, let g  Wpr(
Wpr( ) be arbitrary, and P
) be arbitrary, and P 
 (r) be the Taylor polynomial of g associated to one of the
points in the boundary of
(r) be the Taylor polynomial of g associated to one of the
points in the boundary of  . By some result in §2.6, we have
. By some result in §2.6, we have
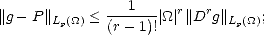 in
particular,
in
particular,
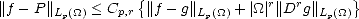 This
gives E(f,
This
gives E(f, (r))p < Cp,rK(f,|
(r))p < Cp,rK(f,| |r;Lp(
|r;Lp( ),Wpr(
),Wpr( )), and application of theorem 19 offers the left inequality in this
case.
)), and application of theorem 19 offers the left inequality in this
case.
The right inequality is trivial for all p, since  r(f,t)p =
r(f,t)p =  r(f -P,t)p < 2r
r(f -P,t)p < 2r 0(f -P,t) = 2r||f -P||Lp(
0(f -P,t) = 2r||f -P||Lp( ) for all
P
) for all
P 
 (r).
(r). ![[#]](msam10-4.gif)
2.8 Other Seminorms for Besov Spaces
Proof. For each dyadic subcube ![[]](msam10-3.gif) j,n, denote
j,n, denote  j,n =
j,n =  n(f)|
n(f)|![[]](msam7-3.gif) j,n the restriction of the piecewise polynomial of
j,n the restriction of the piecewise polynomial of  near-best approximation we get from the operator
near-best approximation we get from the operator  n. In that case,
n. In that case,
Now, for each of the subcubes ![[]](msam10-3.gif) i,n
i,n  Ij,r, we have the estimate therefore,
Ij,r, we have the estimate therefore,
![||f- Tnf||Lp([] ) < Cp,|I | ,n,tE(f,TT(r);Ij,r)p,
j,n j,n](root211x.gif) and
from Whitney’s Theorem and Proposition 10 in page 72, we have Notice that there is a finite number of cubes Ij,r, so the previous sum of averaged moduli of smoothness can be
estimated by the averaged moduli of smoothness on the union: and the statement follows.
and
from Whitney’s Theorem and Proposition 10 in page 72, we have Notice that there is a finite number of cubes Ij,r, so the previous sum of averaged moduli of smoothness can be
estimated by the averaged moduli of smoothness on the union: and the statement follows. ![[#]](msam10-4.gif)
Lemma 2.20 For any 0
< p <  there exist C1,C2 >
there exist C1,C2 > 0
which depend at most on d and p, such that for
all Sn  Xn,
Xn,
![( )
2n sum -1 || [n] ||p 1/p
C1||Sn ||Lp(_O_) < 2-nd|ak,r(Sn)| < C2||Sn||Lp(_O_).
k=1-r](root215x.gif)
Proof. The left hand side is inmediate; given x 
 , let
, let  n(x) = {k
n(x) = {k 
 d | x
d | x  supp(Nk,r[n])} (notice that this value
does not depend on n, but on r and d):
supp(Nk,r[n])} (notice that this value
does not depend on n, but on r and d):
||p|| N [n](x)|| p < C sum ||a[n](S )||px ;
n k (- /\ (x) k,r n k,r p,d,rk (- /\ (x) k,r n supp(N[kn],r)
n n](root216x.gif) hence,
hence,
||p||supp(N[n])||< C 2-nd sum ||a[n](S )||p.
_O_ n p,d,r | k,r n || k,r| p,d,r k=1- r|k,r n|
k (- /\n(x)](root217x.gif) As for
the right inequality, we need to make use of Lemma 2.11 in page 53:
As for
the right inequality, we need to make use of Lemma 2.11 in page 53:
![n n
- nd 2 sum -1 || [n] ||p -nd 2 sum -1 nd
2 |ak,r(Sn)| < 2 2 ||Sn||Lp(Jk,r),
k=1-r k=1-r](root218x.gif) and
the statement follows.
and
the statement follows. ![[#]](msam10-4.gif)
Proposition 12 For any 0
< p <  and r
and r 
 , given f
, given f  Lp
Lp(

)
, there exists C > 0
that depends at most
on p, d and r such that the following estimate holds for all n:
![( n )1/m
wr(f,2-n)p < C2 -nr ||f||m + sum [2krE(f,Xk)p]m ,
Lp(_O_) k=1](root219x.gif) where
where 
= min(1
,p)
.
Proof. Let Sn be an element of best Lp( ) approximation to f from Xn for all n, and s1 = S1, sn = Sn -Sn-1
) approximation to f from Xn for all n, and s1 = S1, sn = Sn -Sn-1  Xn for
n > 2. We can then write f = f - Sn +
Xn for
n > 2. We can then write f = f - Sn +  k=1nsk, and use this inside the difference operator; for suitable h
k=1nsk, and use this inside the difference operator; for suitable h 
 d,
d,
We need to estimate the terms in the sum on the right, but trying to introduce coefficients 2k on
each of the estimates, so that later application of Lemma 1.3 in page 10 is possible; let x 
 (rh):
Now it all relies on estimates of the differences of the basic tensor product puB-splines; these depend heavily on the
location of the point x and the size of |h|; let
(rh):
Now it all relies on estimates of the differences of the basic tensor product puB-splines; these depend heavily on the
location of the point x and the size of |h|; let  (rh) =
(rh) = 

 ', where x
', where x 
 if x and x + rh both belong to the same
subcube
if x and x + rh both belong to the same
subcube ![[]](msam10-3.gif) i,k, and
i,k, and  ' =
' =  (rh) \
(rh) \ 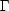 :
:
- If x and x + rh are in the same cube
![[]](msam10-3.gif) i,k
i,k  supp(Nj,r[k]), as Nj,r[k] is a polynomial of coordinate order r
there, we have: where Dhr denotes the derivative in the direction given by h
supp(Nj,r[k]), as Nj,r[k] is a polynomial of coordinate order r
there, we have: where Dhr denotes the derivative in the direction given by h 
 d, and
d, and  x,r,h is a point in the segment with
endpoints x and x + rh. Notice that, although Nj,r[k]|
x,r,h is a point in the segment with
endpoints x and x + rh. Notice that, although Nj,r[k]|![[]](msam7-3.gif) i,n is a polynomial of coordinate order r, its total
degree can be as large as (r - 1)d, and the previous directional derivative is not null in general: A simple
computation gives that for d = 1, the derivative vanishes, but for d > 1, it vanishes if and only if
r < d/(d - 1) < 2.
i,n is a polynomial of coordinate order r, its total
degree can be as large as (r - 1)d, and the previous directional derivative is not null in general: A simple
computation gives that for d = 1, the derivative vanishes, but for d > 1, it vanishes if and only if
r < d/(d - 1) < 2.
In order to estimate ||DhrNj,r[k]||L
 (segment[x,x+rh]), we need to use some basic multivariate calculus: Consider
the univariate polynomial
(segment[x,x+rh]), we need to use some basic multivariate calculus: Consider
the univariate polynomial 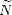 j,r,x,h[k] : [0,1]
j,r,x,h[k] : [0,1] 
 defined by the composition of Nj,r[k](x) = N0,r[0] o
defined by the composition of Nj,r[k](x) = N0,r[0] o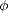 k,j o
k,j o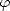 x,h,
where
x,h,
where 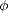 k,j :
k,j :  d
d  x
x  2kx - j
2kx - j 
 d, and
d, and 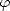 x,h : [0,1]
x,h : [0,1]  t
t  x + rht
x + rht  segment[x,x + rh]
segment[x,x + rh] 
 d.
d.
Use now Markov’s Theorem (page 33) and the fact that ||N0,r[0]||L (
( ) < 1 to obtain ||DhN0,r[0]||L
) < 1 to obtain ||DhN0,r[0]||L (
( ) < Cr;
and therefore, Use this estimate in equation (2.23) to get
) < Cr;
and therefore, Use this estimate in equation (2.23) to get
![| |
||Drh(N [kj,]r,x)|| < Cr(2k| h|)r](root226x.gif)
- Otherwise, if x and x + rh belong to different subcubes of Dk, as far as all the cubes supporting any point
x + ih are contained in the support of Nj,r[k], we simply have Nj,r[k]
 W
W r(
r( ); we can nevertheless apply a
similar estimate as before: therefore,
); we can nevertheless apply a
similar estimate as before: therefore,
![|| r [k] || || ( k(r- 1) r-1)|| k r-1
|Dh(N j,r,x)|< |Dh Cr2 |h| |< Cr(2 |h| ) .](root228x.gif)
We have then,
But ![|| [k]||
|supp(Nj,r)|](root230x.gif) = c2-kd, and |
= c2-kd, and |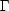 '|< c|h|2-k(d-1); therefore, where
'|< c|h|2-k(d-1); therefore, where  = min(r,r - 1 + 1/p). Using this last estimate on (2.22), we obtain This leads to two different estimates; for k > 2: And for k = 1, We can now find an upper bound on
= min(r,r - 1 + 1/p). Using this last estimate on (2.22), we obtain This leads to two different estimates; for k > 2: And for k = 1, We can now find an upper bound on  r(f,2-n)p using the previous estimates on (2.21): therefore,
r(f,2-n)p using the previous estimates on (2.21): therefore,
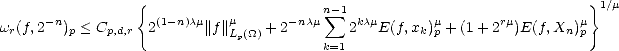 As
both 1 + 2r
As
both 1 + 2r and 2
and 2
 are greater than one for all choices of p and r, we can bound the previous expression
above by multiplying each term in the sum by these coefficients, and include them in the constant.
As we wanted to prove.
are greater than one for all choices of p and r, we can bound the previous expression
above by multiplying each term in the sum by these coefficients, and include them in the constant.
As we wanted to prove. ![[#]](msam10-4.gif)
Remark. Abusing notation, we can denote X0 = {0}, and hence, E(f,X0) = ||f||Lp( ), and we may simplify the
previous estimate to read
), and we may simplify the
previous estimate to read
![( sum n [ ] )1/m
wr(f,2-n)p < Cp,d,r2-nc 2kcE(f,Xk)p m .
k=0](root238x.gif)
Theorem 21 Given r 
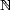 , and 0 < p,q <
, and 0 < p,q < ; then for all 0 <
; then for all 0 <  <
<  , the following quasinorms are equivalent to
the Besov quasinorms ||.||Bq
, the following quasinorms are equivalent to
the Besov quasinorms ||.||Bq (Lp(
(Lp( )) = |.|Bq
)) = |.|Bq (Lp(
(Lp( )) + ||.||Lp(
)) + ||.||Lp( ):
):
where tn(
f) =
Tn(
f)
- Tn-1(
f)
for n > 1
(and of course, T0 
0
).
Proof. The equivalence of N1, N2 and ||.||Bq (Lp(
(Lp( )) follows directly from Proposition 11, Corollary 11.1,
Proposition 12 and the Discrete Hardy’s Inequalities (Lemma 1.3 in page 10). As for the third quasinorm, notice
that on one side,
)) follows directly from Proposition 11, Corollary 11.1,
Proposition 12 and the Discrete Hardy’s Inequalities (Lemma 1.3 in page 10). As for the third quasinorm, notice
that on one side,
therefore, N3(f) < CpN1(f) for all f  Lp(
Lp( ). On the other hand,
). On the other hand,
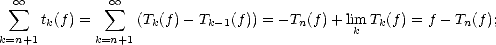 therefore,
therefore,
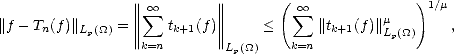 where
where
 = min(1,p). We can use again Lemma 1.3 to obtain
= min(1,p). We can use again Lemma 1.3 to obtain
 which
gives N2(f) < Cq,rN3(f); hence proving the statement.
which
gives N2(f) < Cq,rN3(f); hence proving the statement. ![[#]](msam10-4.gif)
Remark. We have just proved the goal of this chapter; we have precisely determined the approximation spaces in
Lp( ) associated to the family of approximants Xn for all q > 0, and 0 <
) associated to the family of approximants Xn for all q > 0, and 0 <  <
<  :
:
Remark. Theorem 21 offers also the possibility of representing functions in Besov spaces by means of a sequence of
nonnegative real functions satisfying certain properties. We will use this representation to find in the next section an
equivalent expression for the K-functional of couples of Besov spaces; and with it, the computation of interpolation
spaces for such couples.
Notice that 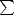 n=1
n=1 tn(f) = limnTn(f) = f a.e.; and as tn(f)
tn(f) = limnTn(f) = f a.e.; and as tn(f)  Xn for each n > 1, we may write
tn(f) =
Xn for each n > 1, we may write
tn(f) =  k=1-r2n-1
k=1-r2n-1
 j,r[n](tn(f))Nj,r[n], and furthermore
j,r[n](tn(f))Nj,r[n], and furthermore
![n
sum oo sum oo 2 sum - 1 [n] [n]
f = tn(f) = aj,r(tn(f ))N j,r
n=1 n=1j=1-r](root245x.gif) | (2.24) |
This atomic decomposition of functions in Bq (Lp(
(Lp( )) leads to yet another equivalent (quasi)norm:
)) leads to yet another equivalent (quasi)norm:
2.9 Further results: K-functional of compatible couples of Besov Spaces
Given a sequence of functions a = (fn)n in a (quasisemi)normed space (X,||.||X), consider for parameters  ,q > 0
the (quasisemi)norms
,q > 0
the (quasisemi)norms
![( oo sum )1/q
|a| laq(X) = [2na||fn||X]q ,
n=0](root247x.gif) and
let
and
let  q
q (X) =
(X) = 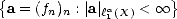 .
.
Consider also, the following operator in Lp( ):
):
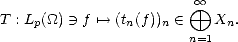 Following Theorem 21, we have that f
Following Theorem 21, we have that f  Bq
Bq (Lp(
(Lp( )) if and only if Tf
)) if and only if Tf 
 q
q (Lp(
(Lp( )), and moreover,
||f||Bq
)), and moreover,
||f||Bq (Lp(
(Lp( ))
)) 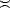 ||Tf||
||Tf|| q
q (Lp(
(Lp( )). We can use this fact to find the K-functionals of compatible couples of Besov
spaces:
)). We can use this fact to find the K-functionals of compatible couples of Besov
spaces:
Theorem 22 Given r 
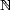 , 0 < p1,q1,p2,q2 <
, 0 < p1,q1,p2,q2 <  , 0 <
, 0 <  1,
1, 2 < r, denote Bi = Bqi
2 < r, denote Bi = Bqi i(Lp
i(
i(Lp
i( )), and
)), and
 i =
i =  qi
qi i(Lp
i(
i(Lp
i( )); then, for all f
)); then, for all f  B1 + B2, there exist constants C1,C2 > 0 which depend at most on
r,d,
B1 + B2, there exist constants C1,C2 > 0 which depend at most on
r,d, 1 and
1 and  2 such that for all t > 0,
2 such that for all t > 0,
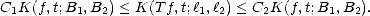
Proof. Let us prove the left inequality: Given f  B1 + B2, let a1 = (an[1])n
B1 + B2, let a1 = (an[1])n 
 1 such that a2 = (an[2])n = Tf -a1
1 such that a2 = (an[2])n = Tf -a1 
 2;
we have K(Tf,t;
2;
we have K(Tf,t; 1,
1, 2) <||a1||
2) <||a1|| 1 + t||a2||
1 + t||a2|| 2. From these sequences ai, we will construct functions fi
2. From these sequences ai, we will construct functions fi  Bi such that
f = f1 + f2, and ||fi||Bi < C||ai||
Bi such that
f = f1 + f2, and ||fi||Bi < C||ai|| i.
i.
We will be using the projectors Tn : L (
( )
)  Xn for both functions fi
Xn for both functions fi  Bi; thus, we need to work in a space
L
Bi; thus, we need to work in a space
L (
( )
)  Lp1(
Lp1( )
)  Lp2(
Lp2( ). As |
). As | | = 1, use Jensen’s Inequality to realize that for each 0 <
| = 1, use Jensen’s Inequality to realize that for each 0 <  < min(p1,p2), and any
function
< min(p1,p2), and any
function 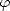
 Lpi, we have
Lpi, we have 
 |
| |
| =
= 

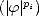
 /pi <
/pi <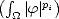
 /pi = ||
/pi = || ||L
pi(
||L
pi( )
) .
.
For each n, let gn = Tn(an[1])  Xn. By the equivalence of quasinorms in finite dimensional spaces, and Proposition
7 in page 54, we know that it must be ||gn||Lp
1(
Xn. By the equivalence of quasinorms in finite dimensional spaces, and Proposition
7 in page 54, we know that it must be ||gn||Lp
1( ) < C
) < C ||gn||L
||gn||L < C
< C ,r,
,r, ||an[1]||L
||an[1]||L (
( ) < C
) < C ,r,
,r, ||an[1]||Lp
1(
||an[1]||Lp
1( ). Consider
now g =
). Consider
now g =  n=1
n=1 gn, which converges trivially in Lp1(
gn, which converges trivially in Lp1( ); notice that for each n, with
); notice that for each n, with  = min(p1,1).
= min(p1,1).
Application of Lemma 1.3 in page 10 gives that it must be
![oo sum na p1 oo sum ( na [1])p1
[2 E(g, Xn)] < Cr,r,t 2 an ;
n=1 n=1](root254x.gif) and therefore, ||g||B1 < C
and therefore, ||g||B1 < C ,r,
,r, ||a1||
||a1|| 1. Similarly, f - g
1. Similarly, f - g  Lp2(
Lp2( ), and with
), and with  = min(p2,1) this time,
and as before, we infere ||f - g||B2 < C
= min(p2,1) this time,
and as before, we infere ||f - g||B2 < C ,r,
,r, ||a2||
||a2|| 2, hence proving the left inequality of the statement.
2, hence proving the left inequality of the statement.
Let us prove the right inequality: Let g  B1 such that f - g
B1 such that f - g  B2. Given
B2. Given  > 0 and 0 <
> 0 and 0 <  < min(p1,p2), we
construct
< min(p1,p2), we
construct  near-best elements of L
near-best elements of L (
( ) approximation to f from Y n via the operator
) approximation to f from Y n via the operator  n : L
n : L (
( )
)  Y n, and using
Lemma 1.5 in page 14, we can obtain as well elements of L
Y n, and using
Lemma 1.5 in page 14, we can obtain as well elements of L (
( ) approximation to g from Y n, say hn(g)
) approximation to g from Y n, say hn(g)  Y n, such
that
Y n, such
that  n(f) - hn(g) are near-best elements of L
n(f) - hn(g) are near-best elements of L (
( ) approximation to f - g from Y n. By an argument
similar to the proof of Lemma 8 in page 55, we realize that Un = Qn(hn(g)) is a near-best Lp1(
) approximation to f - g from Y n. By an argument
similar to the proof of Lemma 8 in page 55, we realize that Un = Qn(hn(g)) is a near-best Lp1( )
approximation to g from Xn, and Rn = Tn(f) - Qn(hn(f)) is a near-best Lp2(
)
approximation to g from Xn, and Rn = Tn(f) - Qn(hn(f)) is a near-best Lp2( ) approximation to f - g from
Xn.
) approximation to f - g from
Xn.
Let un = Un - Un-1 and rn = Rn - Rn-1 for n > 1 (being U0 = R0 = 0 trivially), and consider the sequences
u = (un)n,r = (rn)n 
 n=1
n=1 Xn. Notice that
Xn. Notice that
and similarly, ||rn||Lp
2( ) < Cr,d,
) < Cr,d, ,p2,
,p2, E(f - g,Xn)p2; hence, by Theorem 21 in page 84, we have u
E(f - g,Xn)p2; hence, by Theorem 21 in page 84, we have u 
 1, r
1, r 
 2,
and moreover, for any t > 0, ||u||
2,
and moreover, for any t > 0, ||u|| 1 + t||r||
1 + t||r|| 2 < C
2 < C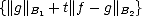 , and the statement follows.
, and the statement follows. ![[#]](msam10-4.gif)
Notice that this result allows us to compute the interpolation spaces for compatible couples of Besov
Spaces. It all depends on the computation of the interpolation spaces 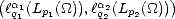
 ,q;
these are easily defined in terms of the Lorentz spaces Lp,q(
,q;
these are easily defined in terms of the Lorentz spaces Lp,q( ), so we will introduce them in the next
section.
), so we will introduce them in the next
section.
2.10 Lorentz spaces
Given a totally  -finite measure space (
-finite measure space ( ,
, ), and values 0 < p,q <
), and values 0 < p,q <  , consider the Lorentz functionals
, consider the Lorentz functionals
and for q =  ,
,
Proof. For all 0 < q < we have trivially
we have trivially  p,q(f) <||f||Lp,q(
p,q(f) <||f||Lp,q( ,
, ), since f*(t) < f**(t) for all t > 0. On the other
hand, for 0 < q <
), since f*(t) < f**(t) for all t > 0. On the other
hand, for 0 < q <  ,
,
A similar proof can be applied for the case q =  .
. ![[#]](msam10-4.gif)
Proof. Part (i) is trivial. Using this, and the subadditivity property of the maximal functions f**, we infere that the
functionals (2.26) and (2.28) are both (quasi)norms for all 0 < q <  .
. ![[#]](msam10-4.gif)
Remark. Notice that the lack of subadditivity of the decreasing rearrangements gives us that the functionals (2.25)
and (2.27) cannot have any (quasi)triangular property; hence, they do not have (quasi)norm structure.
2.11 Further results: Interpolation of Besov Spaces
Proof. We prove first that the integral in the left-hand side is bounded above by the K-functional on the right-hand
side. We will use for this the sub-additivity of the maximal functions ((f + g)**(t) < f**(t) + g**(t) for all t > 0),
and the fact that the spaces Lp( ) are rearrangement-invariant.
) are rearrangement-invariant.
Given f  L1(
L1( ) + L
) + L (
( ), and any decomposition f = f1 + f
), and any decomposition f = f1 + f with fq
with fq  Lq(
Lq( ), we have
), we have
therefore proving the stated inequality.
In order to prove the other inequality, it suffices to find for each t > 0 a decomposition f = f(1,t) + f( ,t) with
f(q,t)
,t) with
f(q,t)  Lq(
Lq( ) such that ||f(1,t)||L1(
) such that ||f(1,t)||L1( ) + t||f(
) + t||f( ,t)||L
,t)||L (
( ) = tf**(t): For this task, fix t > 0, consider
Et = {x
) = tf**(t): For this task, fix t > 0, consider
Et = {x 
 : |f(x)| > f*(t)}, and let t0 = |Et|. Notice that t0 < t trivially, and also f
: |f(x)| > f*(t)}, and let t0 = |Et|. Notice that t0 < t trivially, and also f  L1(Et) (since f is bounded
there). Set g(x) = max{|f(x)|- f*(t),0}signf(x), and h(x) = min{|f(x)|,f*(t)}signf(x).
L1(Et) (since f is bounded
there). Set g(x) = max{|f(x)|- f*(t),0}signf(x), and h(x) = min{|f(x)|,f*(t)}signf(x).
Note first that h  L
L (
( ), with ||h||L
), with ||h||L (
( ) = f*(t). Also, g
) = f*(t). Also, g  L1(
L1( ):
):
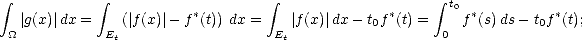 therefore, ||g||L1(
therefore, ||g||L1( ) + t0||h||L
) + t0||h||L (
( ) =
) = 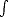 0t0f*(s)ds, and furthermore,
0t0f*(s)ds, and furthermore,
 since
f*(s) = f*(t) for all t0 < s < t.
since
f*(s) = f*(t) for all t0 < s < t. ![[#]](msam10-4.gif)
Corollary 23.2 Given 1
< p1,p2 < ,
, 0
<  <
< 1
and 0
< q < , we have
, we have (
Lp1(

)
,Lp2(

))
 ,q
,q =
Lp,q(

)
,
where 1
/p = (1
- 
)
/p1 +
 /p2.
/p2.
Proof. Use the previous Corollary and the Reiteration Theorem 5 (page 23). ![[#]](msam10-4.gif)
Theorem 24 Let (X,||.||X), (X1,||.||X1) and (X2,||.||X2) be complete (quasi)normed spaces, and let
0 <  1 <
1 <  2, 0 <
2, 0 <  < 1 and 0 < q1,q2 <
< 1 and 0 < q1,q2 < . Denote
. Denote  k(X) =
k(X) =  qk
qk k(X); then the following properties hold:
(i)
k(X); then the following properties hold:
(i) 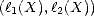
 ,q =
,q =  q
q (X) for all 0 < q <
(X) for all 0 < q < , where
, where  = (1 -
= (1 -  )
) 1 +
1 + 
 2.
(ii)
2.
(ii) 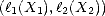
 ,q =
,q =  q
q
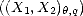 , where
, where  = (1 -
= (1 -  )
) 1 +
1 + 
 2 and 1/q = (1 -
2 and 1/q = (1 -  )/q1 +
)/q1 +  /q2.
/q2.
Corollary 24.1 Under the same hypothesis as in the previous Theorem, if Xk =
Lpk(

)
for 1
< p1,p2 < ,
then we have
,
then we have
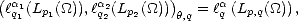 where
where 
= (1
- 
)
 1
1 +

 2,
2, 1
/q = (1
- 
)
 1
1 +

 2, and
2, and 1
/p = (1
- 
)
/p1 +
 /p2.
/p2. ![[]](msam10-3.gif)
Corollary 24.2 Under the same hypothesis as in the previous Corollary, we have
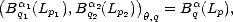 where
where 
= (1
- 
)
 1
1 +

 2,
2, 1
/q = (1
- 
)
/q1 +
 /q2,
/q2, 1
/p = (1
- 
)
/p1 +
 /p2, and p
/p2, and p =
q. ![[]](msam10-3.gif)
2.12 Further Results: Embedding Theorems for Besov Spaces
Theorem 25 Given p, ,
, >
> 0
as in the previous lemma, Bp
(
L
(

))
is continuously embedded in Lp(

)
.
3 Approximation by Ridge Functions on Dyadic maximal-smoothness splines
3.1 General Theory of Ridge Functions
Throughout this section,  d denotes the d-dimensional unit ball in
d denotes the d-dimensional unit ball in  d with respect to the euclidean norm; their d
dimensional size is denoted
d with respect to the euclidean norm; their d
dimensional size is denoted 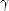 d.
d. 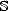 d-1, the unit sphere, is the boundary of the previous set; and
d-1, the unit sphere, is the boundary of the previous set; and 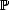 d-1
d-1 
 d-1
is the set of directions in
d-1
is the set of directions in  d. We assume the latter to be a connected set for integration purposses.
d. We assume the latter to be a connected set for integration purposses.
Lemma 3.1 Ridge functions have the following properties:
(i) Given a direction 

 d-1, and any univariate function f, the ridge function
d-1, and any univariate function f, the ridge function 
[
f,
]
is constant over the
intersection of  d with each affine fyperplane which is orthogonal to
d with each affine fyperplane which is orthogonal to  .
(ii)
.
(ii) 
[
 f
f +
g,
] =

[
f,
] +
[
g,
]
for all 

 d-1,
d-1, 

 and univariate functions f,g.
(iii) If f
and univariate functions f,g.
(iii) If f  Lp
Lp(
 1
1)
, then for all 

 d-1,
d-1, 
[
f,
]
 Lp
Lp(
 d
d)
, with ||
[
f,
]
||Lp( d) < Cp,d||f||Lp(
d) < Cp,d||f||Lp( 1) for some
constant C >
1) for some
constant C > 0
that depends at most on d and p.
(iv) Given f :
 d
d 
 and a univariate function g, there exists h
and a univariate function g, there exists h =
hf,g such that f * 
[
g,
] =
[
h,
]
. Moreover, if 1
< q <  , f
, f  Lq
Lq(
 d
d)
, and g  L1
L1(
 1
1)
, then we have ||
[
h,
]
||Lq( d) <
d) <
 d-1||f||Lq(
d-1||f||Lq( d)||g||L1(
d)||g||L1( 1).
1).
Proof.
-
- (i) Given


 d-1, let us denote
d-1, let us denote 
 the affine hyperplane which is orthogonal to
the affine hyperplane which is orthogonal to  and goes through the
origin; we will also denote span{
and goes through the
origin; we will also denote span{ } the line trough the origin with direction
} the line trough the origin with direction  . As
. As  d =
d = 

 span{
span{ },
we can then express each x
},
we can then express each x 
 d uniquely as x = ux +
d uniquely as x = ux + 
 , where ux
, where ux 

 is the orthogonal projection
of x over
is the orthogonal projection
of x over 
 , and
, and 
 is the orthogonal projection of x over span{
is the orthogonal projection of x over span{ }. In that case, we have:
}. In that case, we have:
 = f(h .x) = f(h.ch) = f (c).](root274x.gif)
-
- (ii) is trivial.
-
- (iii) In order to estimate norms of ridge functions for a given direction


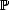 d-1, we will make use of the
tangent cylinders Cyld(
d-1, we will make use of the
tangent cylinders Cyld( ) to the unit spheres and with bases parallel to the hyperplanes
) to the unit spheres and with bases parallel to the hyperplanes 
 (with this
definition, each d dimensional cylinder is unique). Notice that those bases are (d-1) dimensional balls
in
(with this
definition, each d dimensional cylinder is unique). Notice that those bases are (d-1) dimensional balls
in  d. In that case, we may estimate
d. In that case, we may estimate
| pdx = |f(h.x)| pdx < | f(h.x)|pdx = gd- 1 |f(t)| p dt,
_O_d _O_d Cyld(h) _O_1](root275x.gif) what proves our statement.
what proves our statement.
-
- (iv) Given x = ux +



 d as before, we observe that and therefore, this convolution is also a ridge function with the same direction. Denote h = hf,g a univariate
function such that f *
d as before, we observe that and therefore, this convolution is also a ridge function with the same direction. Denote h = hf,g a univariate
function such that f *  [g,
[g, ] =
] =  [h,
[h, ].
].
If f  Lq(
Lq( d) and g
d) and g  L1(
L1( 1), we may estimate,
1), we may estimate,
which is what we wanted to prove. ![[#]](msam10-4.gif)
Definition 23 Given 0
< p <  , and a homogeneous subspace of functions F
, and a homogeneous subspace of functions F  Lp
Lp(
 1
1)
, consider the
following spaces of ridge functions on  d:
Discrete non-linear ridgelets:
d:
Discrete non-linear ridgelets:
![{ sum m }
Ym(F) = /\[fk,hk] : fk (- F,hk (- Pd- 1 .
k=1](root278x.gif) Discrete linear ridgelets:
Discrete linear ridgelets:
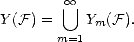 Radon Ridgelets: Let Cd
Radon Ridgelets: Let Cd =
 d-1 ×
d-1 ×  1, and consider the Inverse Radon linear functional R*
1, and consider the Inverse Radon linear functional R* :
M(
Cd)
 M
M(
 d
d)
defined by R*g(
x) =
 d-1g
d-1g(
 ,
, . x
. x)
d :
:
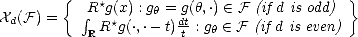
4 Appendix
4.1 Elements of Functional Analysis
4.1.1 Linear Transformations
Proof.
-
(i)
 (ii)
(ii) - By hypothesis there exists
 ,
, > 0 such that ||F(x)||Y <
> 0 such that ||F(x)||Y <  ||x||X for all x
||x||X for all x  X with ||x||X <
X with ||x||X <  .
Given
.
Given  > 0, we can choose
> 0, we can choose  = min(
= min( ,
, /
/ ) > 0 and we have continuity at 0.
) > 0 and we have continuity at 0.
-
(ii)
 (iii)
(iii) - Given
 > 0, choose
> 0, choose  > 0 to satisfy continuity at 0, and given any x
> 0 to satisfy continuity at 0, and given any x  X, consider y
X, consider y  X with
||x - y||X <
X with
||x - y||X <  . We have then ||F(x) - F(y)||Y = ||F(x - y)||Y <
. We have then ||F(x) - F(y)||Y = ||F(x - y)||Y <  , and F is continuous at x. Notice
that the choice of
, and F is continuous at x. Notice
that the choice of  does not depend on the value of x.
does not depend on the value of x.
-
(iii)
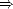 (iv)
(iv) - Given
 = 1, choose the corresponding
= 1, choose the corresponding 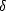 > 0 as in the definition of uniform continuity. Given
x
> 0 as in the definition of uniform continuity. Given
x  X, consider x' =
X, consider x' =  x; notice that ||x'||X =
x; notice that ||x'||X =  /2. Then it must be ||F(x')||Y < 1; therefore
proving the statement:
/2. Then it must be ||F(x')||Y < 1; therefore
proving the statement:
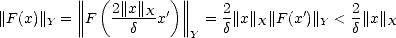
-
(iv)
 (i)
(i) - This is trivial.
-
(iii)
 (v)
(v) - If F is continuous, then since {0} is closed in
 , it must be Z(F) = F-1({0}) closed in X.
Conversely, assume that Z(F) is closed in X and that F is not continuous at 0; then there exists a
sequence (xn)n converging to zero in X and a value
, it must be Z(F) = F-1({0}) closed in X.
Conversely, assume that Z(F) is closed in X and that F is not continuous at 0; then there exists a
sequence (xn)n converging to zero in X and a value  > 0 such that |F(xn)| >
> 0 such that |F(xn)| >  for all n. Consider an
element x0
for all n. Consider an
element x0  X with ||x0||X =
X with ||x0||X =  > 0, and the sequence (yn)n given by yn = x0 -
> 0, and the sequence (yn)n given by yn = x0 -  xn/F(xn). Notice
that F(yn) = 0 for all n (and so yn
xn/F(xn). Notice
that F(yn) = 0 for all n (and so yn  Z(F)), but limnyn = x0 /
Z(F)), but limnyn = x0 / Z(F), a contradiction.
Z(F), a contradiction. ![[#]](msam10-4.gif)
Remark. One should not be very happy about the previous result when dealing with quasinorms; still existence of
continuous linear functionals has to be proved in the space of your choice. For instance, in Lp[0,1] for 0 < p < 1, the
only continuous linear functional is the zero functional! A proof of this result (M. M. Day’s Theorem) can be read
in [Torc].
Corollary 26.1 All linear functionals of a (quasi)normed linear space are continuous.
Proof. This is a direct consequence of (v) in Theorem 26 above. ![[#]](msam10-4.gif)
Theorem 27 Any two (quasi)norms are equivalent in a finite dimensional linear space.
Proof. Given two different (quasi)norms in a finite dimensional linear space Xd, ||.||1 and ||.||2, it will be enough to
prove that the linear function F : (Xd,||.||1)  x
x x
x  (Xd,||.||2) is continuous. For that purpose, choose any basis
of Xd, say {fk}k=1d, and decompose F in terms of the projections over the coordinate subspaces span(fk):
F(.) =
(Xd,||.||2) is continuous. For that purpose, choose any basis
of Xd, say {fk}k=1d, and decompose F in terms of the projections over the coordinate subspaces span(fk):
F(.) =  k=1dprojk(.)fk. We have written F as a finite sum of continuous functionals (by the previous
Corollary); hence, F must be continuous. Apply now part (iv) of Theorem 26 to get the desired result.
k=1dprojk(.)fk. We have written F as a finite sum of continuous functionals (by the previous
Corollary); hence, F must be continuous. Apply now part (iv) of Theorem 26 to get the desired result. ![[#]](msam10-4.gif)
Corollary 27.1 Every closed bounded set of a finite dimensional (quasi)normed linear space is compact.
4.1.2 The Hahn-Banach Theorem
4.2 Rearrangement-Invariant spaces
4.2.1 Riesz Spaces
Let ( ,
, ) be a measure space; consider the following sets:
) be a measure space; consider the following sets:
-
- M(
 ,
, ), the set of measurable functions on
), the set of measurable functions on  .
.
-
- M+(
 ,
, ), the set of nonnegative measurable functions.
), the set of nonnegative measurable functions.
-
- M0(
 ,
, ), the set of measurable functions f such that
), the set of measurable functions f such that  {|f| =
{|f| =  } = 0.
} = 0.
A mapping  : M+
: M+  [0,
[0, ] is called a quasinorm function, if for f,g
] is called a quasinorm function, if for f,g  M+(
M+( ,
, ), the following properties
hold:
), the following properties
hold:
 is a quasinorm.
is a quasinorm.
- If g < f (
 - a.e.), then
- a.e.), then  (g) <
(g) <  (f).
(f).
- If (fn)n
 M+(
M+( ,
, ) verifies fn+1 > fn (
) verifies fn+1 > fn ( - a.e.) for all n, and limnfn = f (
- a.e.) for all n, and limnfn = f ( - a.e.), then also
limn
- a.e.), then also
limn (fn) =
(fn) =  (f).
(f).
- For any measurable subset E

 with
with  (E) <
(E) <  ,
,  (
( E) <
E) <  .
.
- For E

 as before, there exists a constant CE > 0 such that
as before, there exists a constant CE > 0 such that  Ef d
Ef d < CE
< CE (f) for all f.
(f) for all f.
Given such a quasinorm function on ( ,
, ), the collection X(
), the collection X( ) = {f
) = {f  M(
M( ,
, ) |
) |  (|f|) <
(|f|) <  } is called a Riesz
space associated to
} is called a Riesz
space associated to  . Such spaces inherit from its quasinorm special properties:
. Such spaces inherit from its quasinorm special properties:
- Lattice property: if |g|<|f|, then
 (g) <
(g) <  (f).
(f).
- Fatou’s property: Let f,(fn)n
 M+(
M+( ,
, ) such that limnfn = f. If f
) such that limnfn = f. If f  X(
X( ), then limn
), then limn (fn) =
(fn) =  (f);
otherwise, limn
(f);
otherwise, limn (fn) =
(fn) =  .
.
- Fatou’s Lemma: Given (fn)n
 M(
M( ,
, ),
),  (liminf nfn) < liminf n
(liminf nfn) < liminf n (fn).
(fn).
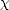 E
E  X(
X( ) for all measurable subset E
) for all measurable subset E 
 with
with  (E) <
(E) <  ; besides, there exists a constant CE > 0
such that
; besides, there exists a constant CE > 0
such that  Ef d
Ef d < CE
< CE (f) for all f
(f) for all f  X(
X( ).
).
- Every convergent sequence in X(
 ) has a
) has a  - a.e. convergent subsequence.
- a.e. convergent subsequence.
- Riesz-Fisher property: If
 n=1
n=1
 (fn) <
(fn) <  , then
, then  n=1
n=1 fn converges in X(
fn converges in X( ) to a function
f
) to a function
f  X(
X( ), and
), and  (f) <
(f) <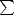 n=1
n=1
 (fn).
(fn).
4.2.2 Resonant measure spaces
Definition 24 Given a measurable space ( ,
, ), and f
), and f  M(
M( ,
, ), consider the associated functions:
), consider the associated functions:
-
- Distribution.
 f : (0,
f : (0, )
)  y
y

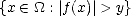
 (0,
(0, ).
).
-
- Decreasing Rearrangement. f* : [0,
 )
)  t
t inf y>0
inf y>0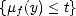
 [0,
[0, ).
).
-
- Maximal function. f** : (0,
 )
)  t
t
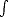 0tf*(s)ds
0tf*(s)ds  (0,
(0, ).
).
We say two measurable functions f,g are equimeasurable (and we write f ~ g), if  f =
f =  g.
g.
Lemma 4.2 (Properties of the decreasing rearrangement) Given f,g  M
M(
 ,
,
)
,
- f* is a nonnegative, right-continuous decreasing function.
- If |g|<|f|(
 - a.e.), then g*< f*.
- a.e.), then g*< f*.
- (af)* = |a|f* for all a

 .
.
- (f + g)*(t + s) < f*(t) + g*(s) for all t,s > 0.
- Fatou’s property: If |f|< liminf n|fn|(
 - a.e.), then also f* < liminf nfn*; in particular, if (fn)n
verifies |fn+1|>|fn| for all n, and limn|fn| = |f|(
- a.e.), then also f* < liminf nfn*; in particular, if (fn)n
verifies |fn+1|>|fn| for all n, and limn|fn| = |f|( - a.e.), then limnfn* = f*.
- a.e.), then limnfn* = f*.
- f ~ f*.
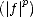 * =
* = 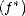 p for all 0 < p <
p for all 0 < p <  .
.
- For all f
 M0(
M0( ,
, ) and 0 < p <
) and 0 < p <  ,
,
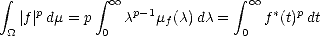
- esssup
 |f| = inf{
|f| = inf{ |
|  f(
f( ) = 0} = f*(0).
) = 0} = f*(0).
- Weak subadditivity: (f + g)*(t + s) < f*(t) + g*(s) for all t,s > 0.
Remark. These three new functions associated to f may be used to perform integral operations on f, but in a
simpler setup. The three subsequent results show us how:
Example. Consider  = {1,...,n} with measure
= {1,...,n} with measure  :
: 
 k
k 1/n for all k. Notice that, given any measurable
function g :
1/n for all k. Notice that, given any measurable
function g : 
 k
k gk
gk 
 , then any
, then any 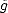 ~ g may be obtained by mere permutation of the elements (there
exists a permutation
~ g may be obtained by mere permutation of the elements (there
exists a permutation 

 n such that
n such that 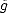 k = g
k = g (k)). In this case, equality is attained in Corollary 13.1:
Given f = (f1,...,fn), consider a permutation
(k)). In this case, equality is attained in Corollary 13.1:
Given f = (f1,...,fn), consider a permutation  such that |f
such that |f (k)|>|f
(k)|>|f (k+1)| for all k; then we have
(k+1)| for all k; then we have
 f =
f = 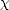 [0,|f
[0,|f
 (n)|) +
(n)|) +  k=1n-1
k=1n-1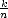
 [|f
[|f (k+1)|,|f
(k+1)|,|f (k)|), and f* =
(k)|), and f* =  k=1n|f
k=1n|f (k)|
(k)|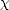 [(k-1)/n,k/n); therefore, for any given
g = (g1,...,gn), it suffices to find two permutations: first
[(k-1)/n,k/n); therefore, for any given
g = (g1,...,gn), it suffices to find two permutations: first  ' permutes the indices so that |g
' permutes the indices so that |g '(k)|>|g
'(k)|>|g '(k+1)|, and
then
'(k+1)|, and
then  matches
matches  '(k) with
'(k) with  (k). This gives us, for
(k). This gives us, for 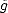 k = g
k = g (k), that
(k), that
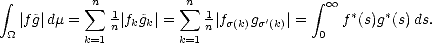
Definition 25 We say a measure space ( ,
, ) is resonant if
) is resonant if
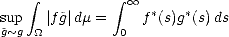 for all f,g
for all f,g  M0
M0(
 ,
,
)
. We say the space is strongly resonant
if the supremum is attained.
We will prove that any compact cube 

 d with the Lebesgue measure is a strongly resonant space, and
therefore we may use the previous results to simplify the computation of integral operations on it:
d with the Lebesgue measure is a strongly resonant space, and
therefore we may use the previous results to simplify the computation of integral operations on it:
Proposition 14 Any cube in  d with the Lebesgue measure is a strongly resonant space.
d with the Lebesgue measure is a strongly resonant space.
Definition 26 Given a totally  -finite measure space
-finite measure space (
 ,
,
)
, a quasinorm function 
:
M+(
 ,
,
)

 +
such that
+
such that 
(
f) =

(
g)
for each f ~ g  M0+
M0+(
 ,
,
)
is called rearrangement-invariant
. In that case, the space
X(

)
is said to be rearrangement-invariant
as well.
Notice that the spaces Lp for any 0 < p < are all rearrangement-invariant.
are all rearrangement-invariant.
4.3 To Do
- We need the proof of the Reiteration Theorem (page 5) for
 ,q interpolation spaces via the real method
of Peetre and Lions, and the previous result. It will be used in section 2.11.
,q interpolation spaces via the real method
of Peetre and Lions, and the previous result. It will be used in section 2.11.
- Perhaps a more exhaustive reading on the paper by Brown and Lucier. Mainly the characterization
of best-approximations in L1 and the main theorem.
- Finish the proof of the Lemma on mollifiers in section 2.6.1.
- Maybe include the construction of several K-functionals; this will give you the opportunity of presenting
the Rearrangement-Invariant spaces and its applications. If you want to prove Whitney’s Theorem,
then you must show the K-functional for the pair (Lp,Wpr).
- Prove the results in section 4.1.2, and include a few corollaries. Which ones? I am not sure; among the
ones I have in Friedman and Prof. Philips’ notes, it is possible that there are some that have interest
for Approximation Theory. Sit on it for a while.
- Finish the proofs of the results in section 2.7.1 on Besov Spaces.
- Extend the results in section 1.3 using chapter 3 of [DeLo]. Theorem 1.3 and its implications to best
approximation in Lp for 1 < p <
 set an idea of what one can or cannot require of (near)best
operators; namely, linearity, continuity, boundedness, and how to use those properties to construct
(near)best approximations to any given function. This is a good spot to include item 2, although it
might be even better in section 2.1.
set an idea of what one can or cannot require of (near)best
operators; namely, linearity, continuity, boundedness, and how to use those properties to construct
(near)best approximations to any given function. This is a good spot to include item 2, although it
might be even better in section 2.1.
- Maybe prove all the claims in section 4.2.2; for completion, mainly. Or the reader can be directed to
the proofs in [BeSh] if interested.
- Finish the missing proofs in section 2.6.3 related to the equality of spaces Hpr(G) = Wpr(G).
References
[Adam] R.A. Adams, “Sobolev Spaces”, Academic Press, New York, 1975.
[deBo] C. de Boor, “Class notes for Math/CS 887, Spring’03”, http://www.cs.wisc.edu/~deboor.
[dBFi] C. de Boor and G.F. Fix, “Spline approximation by quasi-interpolants”, J. Approx. Theory 8
(1973), 19-45.
[BeSh] C. Bennet and R. Sharpley, “Interpolation of Operators”, Academic Press (1988), New York.
[BrLu] L. Brown and B. Lucier, “Best approximations in L1 are near best in Lp, p < 1”,
Proc. Amer. Math. Soc. 120 (1994), 97-100.
[Bure] V.I. Burenkov, “Sobolev Spaces in Domains”, http://www.cf.ac.uk/maths/people/Sobol.pdf
[Cal1] A.P. Calderón, “Intermediate spaces and interpolation: the complex method”, Studia Math. 24
(1964), 113-190.
[Cal2] A.P. Calderón, “Spaces between L1 and L and the Theorem of Marcinkieiwicz: the complex
method”, Studia Math. 26 (1964), 273-279.
and the Theorem of Marcinkieiwicz: the complex
method”, Studia Math. 26 (1964), 273-279.
[CDeH] A. Cohen, R. DeVore and R. Hochmuth, “Restricted Approximation”, Constr. Approx. 16
(2000), no. 1, 85-113.
[CuSc] H. B. Curry, I. J. Schoenberg, “On Pólya frequency functions. IV. The fundamental spline
functions and their limits”, J. Analyse Math 17 (1966), 71-107.
[DeVo] R. DeVore, “Nonlinear Approximation”, Acta Numerica 7 (1998), 51-150.
[DeLo] R. DeVore and G. Lorentz, “Constructive Approximation”, Springer Grundlehren, Heidelberg,
1993.
[DeP1] R. DeVore and V. Popov, “Interpolation of Besov Spaces”, Trans. Amer. Math. Soc. 305
(1988), 397-414.
[DeP2] R. DeVore and V. Popov, “Interpolation spaces and nonlinear approximation”, Function Spaces
and Applications (M. Cwikel et al., eds), Vol. 1302 of Lecture Notes in Mathematics, Springer, Berlin,
191-205.
[DeSh] R. DeVore and R. Sharpley, “Maximal Functions Measuring Smoothness”, Memoirs Vol. 293
(1984), American Mathematical Society, Providence, RI.
[Frie] A. Friedman, “Foundations of Modern Analysis”, Dover, New York, 1982.
[Peet] J. Peetre, “A Theory of Interpolation of Normed Spaces”, Course notes, University of Brasilia
(1963).
[Petr] P. Petrushev, “Approximation by Ridge Functions and Neural Networks”, SIAM J. on Math
Analysis, 30 (1998) 115-189.
[Torc] A. Torchinsky, “Real Variables”, Addison-Wesley, 1988.
 d
d

 X
X
 E
E ,q >
,q > 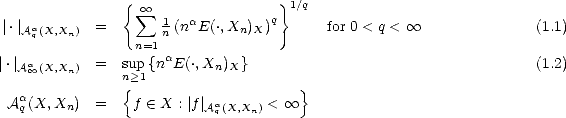


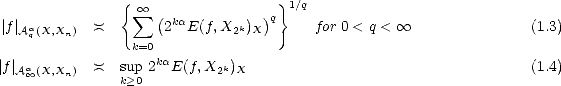
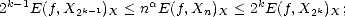
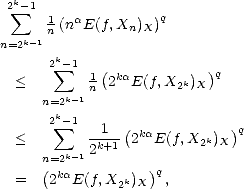
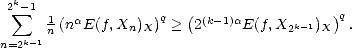
![[#]](msam10-4.gif)

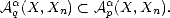


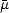 ), where
), where 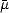 (
(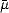 )) functions
)) functions

 2
2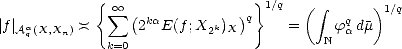


![(i ntegral )1/p
|f| a )( fp dm < ||f || ||f || )( |f |a | f |a [#]
A p(X,Xn) N a a l oo a lq A oo (X,Xn) Aq(X,Xn)](root12x.gif)
![integral oo ( -a integral t ds)q dt 1 integral oo [- a ]q dt
t f(s)-s -t < aq- t f(t) -t (1.5)
integral 0 oo ( integral 0 oo )q integral 0 oo
ta f(s)ds dt < 1q- [taf(t)]q dt (1.6)
0 t s t a 0 t](root13x.gif)
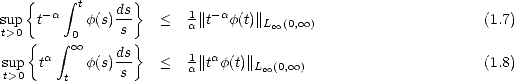
![integral integral (i ntegral )1/q( integral )1/p
tf(s)ds = ts- cf(s)sc-1ds < t[s-cf(s)]qds tsp(c- 1)ds
0 s 0 0 0](root15x.gif)
![integral t- p(1-c) 1-p(1-c)]t
s ds = Cq,c s s=0
0](root16x.gif)

![integral oo ( integral t )q
t-aq f(s)ds dt
0 integral 0 s t integral
oo -aq-1q/p-q+cq t[- c ]q
< Cq,c 0 t t 0 s f(s) dsdt
integral oo integral t[ ]q
= Cq,c tq(c-a)-2 s-cf(s) ds dt
integral 0 oo [ ] 0 integral oo
= Cq,c s-cf(s)q tq(c-a)-2dtds
0 s](root17x.gif)
![integral oo [ integral t ]q integral oo
t-a f(s)ds dt < Cq,a,c [s-af(s)]q ds
0 0 s t 0 s](root18x.gif)
![[t-af(t)]](root19x.gif)
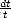 when the functions
when the functions ![integral oo [ ]q dt sum integral 2k+1[ ]q dt sum
t-af(t) t-= k t- af(t) -t )( 2aqkf(2-k)q.
0 k (- Z 2 k (- Z](root21x.gif)
 ,
,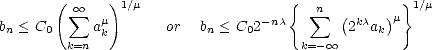
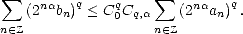



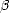 <
< 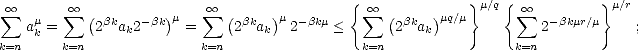
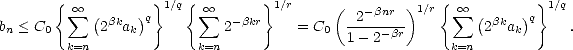
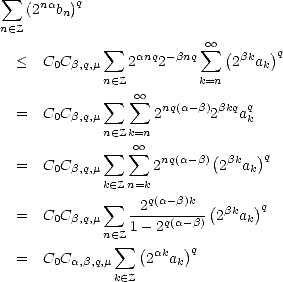
![integral oo ( - a integral t ds)q dt integral oo [ -a ]q dt
t f(s)s- t- < C t f(t) t- (1.9)
integral 0 oo ( integral 0 oo )q integral 0 oo
ta f(s)ds dt < C [taf(t)]q dt (1.10)
0 t s t 0 t](root27x.gif)
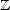
![integral t ds integral 2- n ds sum oo integral 2-k ds
f(s)-s < f(s)-s < -(k+1) f(s)s
0 0 k=n 2
oo sum -k 2- k sum oo -k
= f(2 ) log(s)]2- (k+1) = (log2) f(2 ).
k=n k=n](root28x.gif)
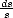 ,
, 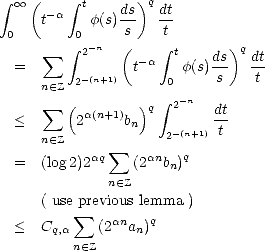
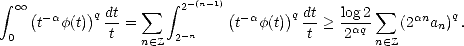


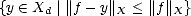 .
. ![-1
Yf = F (- oo , ||f||X], where F : Y -) y '--> ||f - y|| X (- R](root33x.gif)
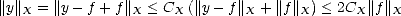
!['
||y- z ||X
= ||y - x- z''+ x - z||X
< CX {||y - x- z''||X + ||x- z||X}
< C {E(y - x,Z) + tE(x,Z) }
X X X''' ''
< CX,t {E(y- x,Z)X + ||x -(z - z )||X}
= CX,t {E(y- x,Z)X + ||x -y + y+ z''-z'''||X}
< CX,t {E(y- x,Z)X + CX [||x- y +z''||X + ||y -z'''||X]}
< C {E(x- y,Z) + E(y,Z) }
X,t X X
< CX,tE(y,Z)X [#]](root35x.gif)
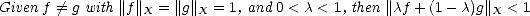
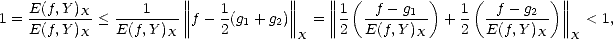
 >
> 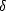
![||f(f )- f(g)|| X
= ||f(f)- f + f - g+ g -f(g)||X
< C2 {||f(f)- f||X + ||f- g||X + ||g- f(g)||X}
X2
< 3CX ||f - g||X < e [#]](root38x.gif)
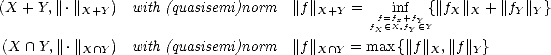
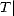
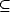

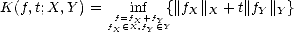
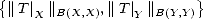
![||f || +t||f ||
X X Y Y
= [c + (1 - c)]|| fX ||X +[ct1 + (1- c)t2]||fY||Y
= c{||fX||X + t1||fY||Y}+ (1 -c) {||f||X + t2||fY||Y}
> cK(f,t1;X,Y )+ (1 - c)K(f, t2;X, Y)](root45x.gif)
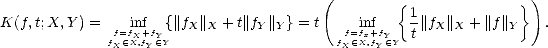
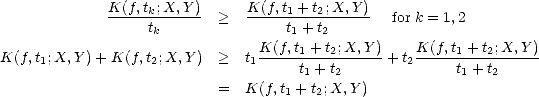
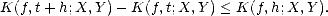
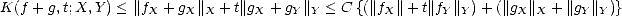
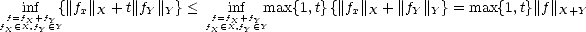
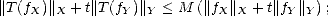
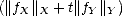 , which proves the desired result.
, which proves the desired result.  <
< 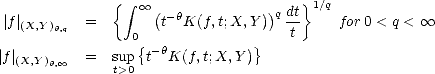
 ,q
,q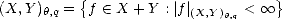
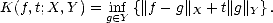
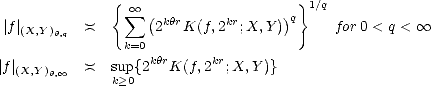
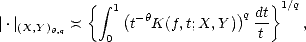
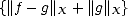
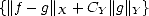 , and therefore,
, and therefore,
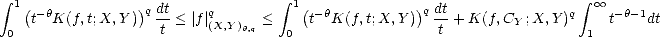
![( integral t )1/q1 (i ntegral oo )1/q2
K(f, td;Y1,Y2) )( [s-a1K(f,s;X1,X2)]q1 ds + td [s-a2K(f,s;X1,X2)]q2 ds ,
0 s t s](root61x.gif)
 ,q
,q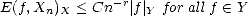
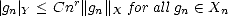
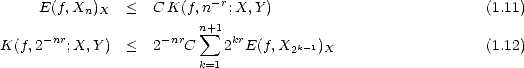
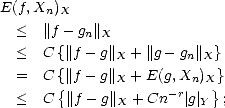
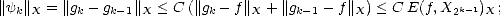
![K(f, 2-nr;X,Y )X
< ||f- g || + 2-nr| g |
n X n|| Yn ||
= E(f,X n) + 2-nr|| sum y ||
2 X |k=0 k|
n Y
< E(f,X2n)X + 2-nrC sum |yk|Y
k=1
(since y0 = g0 = 0)
n sum
< E(f,X2n)X + 2-nrC 2krE(f,X2k- 1)X
k=1
n+ sum 1
< 2-nrC 2krE(f,X2k -1)X [#]
k=1](root67x.gif)
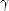 < r
< r 
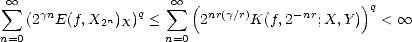
![sum oo ( )q
2nr(g/r)K(f,2-nr;X,Y )
n=0
sum oo q
= (2gnbn)
n=0
sum oo gn q
< C (2 an)
n= oo 0
= C sum (2gnE(f,X n) )q [#]
n=0 2 X](root69x.gif)
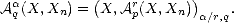
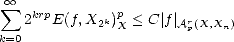
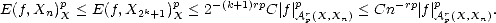
![p
|gn|Arp(X,Xn)
sum oo p
= 1k (krE(gn,Xk)X)
k=1
n sum - 11 r p
< k (k | gn|X)
k=1
p n sum -1 rp-1
= |gn|X k
k=1
p n sum -1 rp-1
< |gn|X (n- 1)
k=1r p
= [(n- 1) | gn|X]
< (nr|gn| X)p .](root73x.gif)
![||f - Tnf||X + n-r|Tnf| Y < C K(f,n -r;X, Y) for all f (- X. []](root74x.gif)

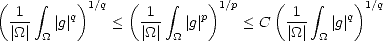
 (
( )
)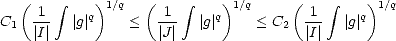
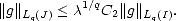
![||f - g||Lp(_O_() )
< Cd,p ||f - P||Lp(_O_) + ||P- g||Lp(_O_)
(apply Lemma 2.1)
( 1/p-1/q )
< Cd,p E(f, TT(r);_O_)p + Cd,q,r|_O_| ||P- g||Lq(_O_)
( 1/p-1/q [ ])
< Cd,p,q,r E(f,TT(r);_O_)p + |_O_ | ||P - f||Lq(_O_) + ||f- g||Lq(_O_)
< C (E(f,TT(r);_O_) + |_O_ |1/p-1/q [||f - P|| + tE(f,TT(r);_O_) ])
d,p,q,r( p Lq(_O_) ) q
< Cd,p,q,r E(f,TT(r);_O_)p + 2max(1,t)|_O_|1/p-1/q|| f - P||L (_O_)
q
(apply Ho¨l(der’s Inequality or Lemma 2.1) again)
< Cd,q,p,r,t E(f,TT(r);_O_)p + ||f- P ||Lp(_O_)
= Cd,q,p,r,tE(f,TT(r);_O_)p. [#]](root78x.gif)
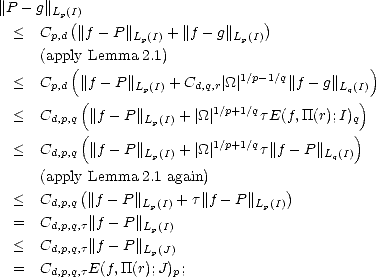
![||f- g||Lp(J() )
< Cp,d ||f- P ||Lp(J) + ||P - g||Lp(J)
(apply Lemma 2.2)
( 1/p )
< Cp,d E(f,TT(r);J)p + c Cp,d||P - g||Lp(I)
< Cd,p,q,t,cE(f, TT(r);J)p. [#]](root80x.gif)
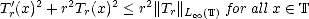


![|P'r(x)| < r||P V~ r||L oo [--1,1].
1- x2](root82x.gif)

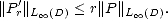
![||P'r||L oo [- 1,1] < r2|| Pr||L oo [-1,1].](root84x.gif)
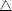
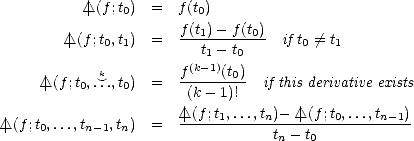
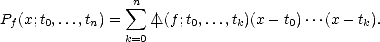
![Pf(x;t0,...,tk+1) = Pf(x;t0,...,tk)+ | /_\ (f;t0,...,tk+1)(x- t0)...(x - tk). [#]](root87x.gif)

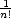
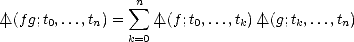
![Ph(x;t0,...,tn)
= Pf (x;t0,...,tn)Pg(x;t0,...,tn)
[n sum ]
= | /_\ (f;t0,...,tk)(x- t0)...(x - tk)
k=0[ ]
sum n
× | /_\ (g;tl+1,...,tn)(x- tl+1)...(x- tn) (2.2)
l=0](root90x.gif)

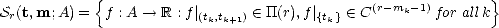

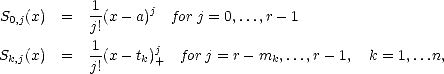
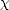
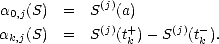

![Sr(t;[0.1]) = Sr({0,1/2,1},{3,3,3};[0,1]).](root96x.gif)

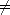
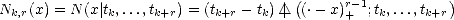
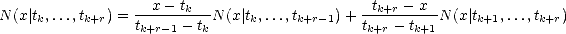
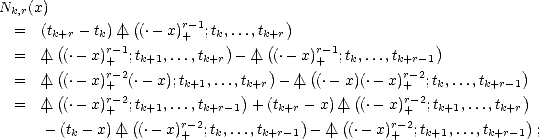
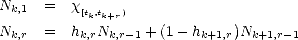
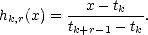



![n
sum Nk,r(x)| [a,b] = x
k=1- r [a,b]](root107x.gif)
![sum n
Nk,r| [a,b]
k=1-r
sum n [ ]
= hk,rNk,r-1| [a,b] + (1 - hk+1,r-1)Nk+1,r-1|[a,b]
k=1-r
n sum
= h1-r,rN1 -r,r-1| [a,b]+(1- hn+1,r- 1)Nn+1,r-1|[a,b]+ Nk,r-1|[a,b]
--0 in [a,b] --0 in [a,b] k=2- r
n
= sum N |
k=2-r k,r-1[a,b]](root108x.gif)
![n n
sum Nk,1| [a,b] = sum x = x
k=0 k=0 [tk,tk+1) /~\ [a,b] [a,b]](root109x.gif)
![n
--1---(q- x)r-1| = sum g (q)N (x)| ,
(r - 1)! [a,b] k=1- r k,r k,r [a,b]](root110x.gif)
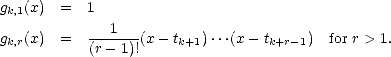
![n sum
gk,r(q)Nk,r| [a,b]
k=1-r
sum n [ ]
= gk,r(q)hk,rNk.r-1|[a,b] + (1- hk+1,r)Nk+1,r- 1| [a,b]
k=1-r
sum n
= [gk,r(q)hk,r + gk-1,r(q)(1- hk,r)]Nk,r-1|[a,b]
k=2-r](root112x.gif)
![gk- 1,r(q) +[gk,r(q)- gk- 1,r(q)]hk,r(x)
= gk-1,r(q)+ gk,r-1(q)(tk- tk+r-1)hk,r(x)
t - x
= gk-1,r(q)+ -k---gk,r-1(q)
r - 1
= q--tkgk,r- 1(q)+ tk--x-gk,r-1(q)
r- 1 r- 1
= q--x-gk,r-1(q);
r - 1](root113x.gif)
![n sum q---x sum n (q--x)r-1
gk,r(q)Nk,r(x)|[a,b] = r- 1 gk,r- 1(q)Nk,r- 1(x)| [a,b] = (r- 1)!
k=1- r k=2-r](root114x.gif)
![n sum r sum -1
P = gk,r(P )Nk,r| [a,b], where gk,r(P) = (-1)ng(r- n- 1)(q)P (n)(q).
k=1- r n=0 k,r](root115x.gif)
![n
(q---x)-
n! ( )
= Dr-1-n (q--x)r-1
(r- 1)!
( sum n )
= Dr-1-n gk,r(q)Nk,r(x)| [a,b]
k=1-r
sum n
= g(r-n-1)(q)Nk,r(x)| [a,b].
k=1-r](root116x.gif)
![r sum -1 (x- q)n r sum -1 sum n (r-n-1)
P (x) = P(n)(q)---n!-- = (- 1)nP (n)(q) gk,r (q)Nk,r(x)| [a,b],
n=0 n=0 k=1- r](root117x.gif)
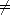
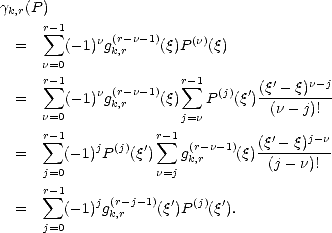
![n n sum
(x--tj)+-= (- 1)n g(rk,-rn-1)(tj)Nk,r(x)| [a,b].
n! k=j](root121x.gif)
![(x - tj)n+
---n!---
(tj -x)n
= (-1)n---n!--x(tj,b]
sum n
= (-1)n g(kr-,r n- 1)(tj)Nk,r(x)|[a,b] /~\ (tj,b]
k=1-r
sum n
= (-1)n g(kr-,r n- 1)(tj)Nk,r(x)|[a,b],
k=j](root122x.gif)
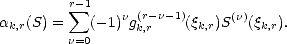
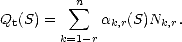
![||Qt(S)||||Lp[a,b] ||
|||| n sum ||||
= |||| ak,r(S)Nk,r||||
k=1- r Lp[a,b]
|||| sum n ||||
< max |ak,r(S)||||| Nk,r||||
0<k<r-1 ||k=1-r ||Lp[a,b]
(notice ak,r is a continuous linear operator
over a finite dimensional space of dimension
r+ n; therefore, they are bounded)
< Cr,n||S||Lp[a,b]||1||Lp[a,b]
< C |b- a| 1/p||S||
r,n Lp[a,b]](root125x.gif)
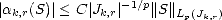
![|ak,r(S|)| |
||r sum -1 n (r-n-1) (n) ||
= || (-1) gk,r (qk,r)S (qk,r)||
n=0
r sum -1 (r- n- 1) (n)
< |gk,r (qk,r)|||S ||L oo (Jk,r)
n=0
(apply Markov ’s Theorem and find a
common bound of the functions gk,r)
r sum -1
< Cr ||S||L oo (Jk,r)
n=0
(apply Lemma 2.1 [page 30])
< Cr |Jk,r|-1/p|| S ||L(J ) [#]
p k,r](root127x.gif)
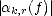
![||Qt(f)||Lp[tj,tj+1] < C ||f||Lp(Ij,r) (2.3)
||Q (f )|| < C ||f|| (2.4)
t Lp[a,b] Lp[a,b]](root129x.gif)
![||Qt(f)||Lp[tj,tj+1]
|||| sum n ||||
= |||| ak,r(f )Nk,r||||
||k=1-r ||L [t ,t ]
|||| pn j j+1||||
< max |a (f)||||| sum N ||||
0<k<r-1 k,r ||k=1- r k,r||
Lp[tj,tj+1]
< Cr 0m<akx<r-1| Jk,r|-1/p||f||Lp(Jk,r)||x[tj,tj+1]|| Lp[a,b]
- 1/p 1/p
< Cr(tk+r- tk) ||f||Lp(Ij,r)(tk+r- tk)](root130x.gif)
![p
||Qt(f)||Lp[a,b]
sum n p
= ||Qt(f)||Lp[tk,tk+1]
k=1-r
sum n p
< Cr ||f ||Lp(Ik,r)
k=1-r
(apply the fact that on each interval Ij,r
there are preciselly r subintervals Jk,r;
therefore, we reduce the previous sum to
a sum over mutually disjoint intervals
that sum add up to [a,b])
< rCr ||f||p
p Lp(Ij,r)
= Cr||f||Lp[a,b] [#]](root131x.gif)




 = sum a (q )DnS(q ), where a (q ) = (-1)|n|g(r-n1-1)(q )...g(r-nd- 1)(q ).
k,r n=0 n,k,r k,r k,r n,k,r k,r k1,r k1,r kd,r kd,r](root136x.gif)
![sum sum
S = cjN [nj,]r + Nkd,r cj'N[jn',]r.
jd/=kd j' (- Zd- 1](root137x.gif)
![r sum -1 ( sum )
akd,r(S) = (-1)n1g(r-n1-1)(qkd,r) cj'N[n'] Dn1Nkd,r(qkd,r).
n1=0 kd,r j' (- Zd-1 j,r](root138x.gif)
![[n] [0] n
N k,r(x) = N 0,r(2x - k)](root139x.gif)

![[]](msam10-3.gif)

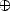

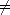
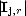 = 2
= 2![|[]j,n|](root144x.gif) . Also, and as before,
the number of subcubes
. Also, and as before,
the number of subcubes || < 2nd/pC||P || . []
k,r Lp(Jk)](root145x.gif)
![||Q (P )|| < c||P|| (2.5)
n Lp([]j,n) Lp(Ij,r)
||Qn(P )|| Lp(_O_) < c||P||Lp(_O_) (2.6)
||P - Qn(P )|| L ([] ) < cE(P;TT(r;Ij,r))p (2.7)
p j,n](root146x.gif)
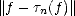
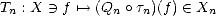
![||t(f)||
n Lp{([]j,n) }
< Cp ||t{n(f)- f||Lp([]j,n) + ||f||Lp([]j,n)}
< Cp,t E(f,TT(r);[]j,n)p + ||f||Lp([]j,n)
< Cp,t||f|| ;
Lp([]j,n)](root149x.gif)
![sum 2n
||Tn(f)||pLp(_O_) = ||Qn(tn(f))|| pLp(_O_) = ||Qn(tn(f))||pLp([]j,n)
j=1
(apply estimate (2.5) above)
2n 2n
< Cr,d,p sum ||tn(f)|| p < Cr,d,p,t sum ||f||p
j=1 Lp(Ij,r) j=1 Lp(Ij,r)
(independence of n is guaranteed, see description of I )
p j,r
< Cr,d,p,t||f||Lp(_O_)](root150x.gif)
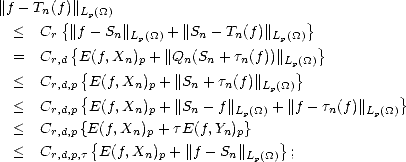
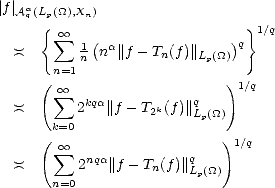


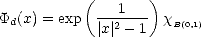

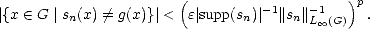
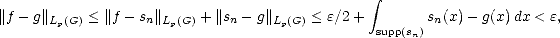
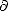 G
G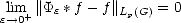


 /
/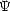



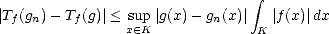
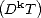 (
(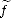
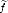
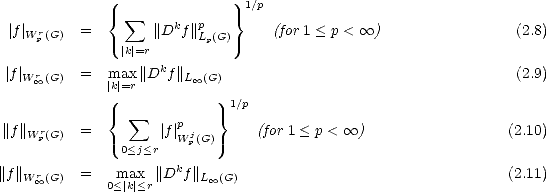
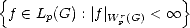
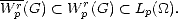
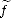
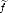
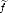
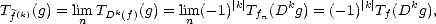
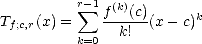
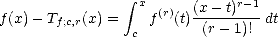
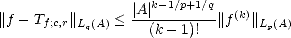
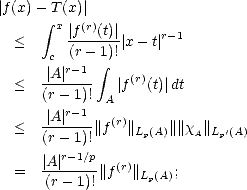
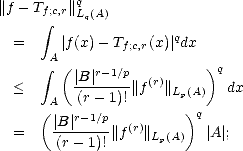
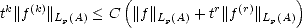
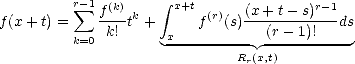
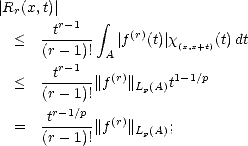
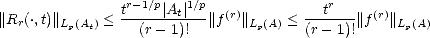
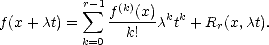

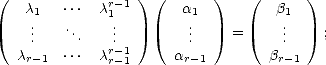
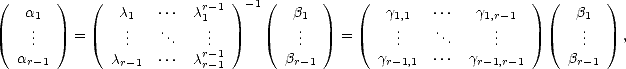
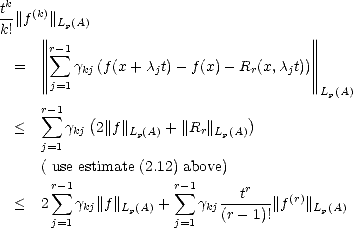
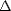
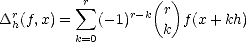
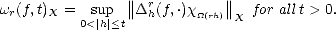

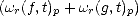 , with the same constant from the
(quasi)triangular inequality in
, with the same constant from the
(quasi)triangular inequality in 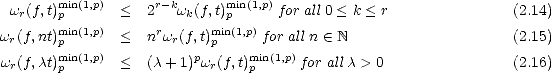
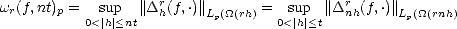
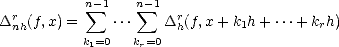
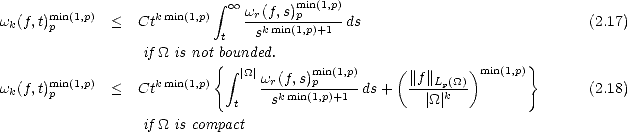
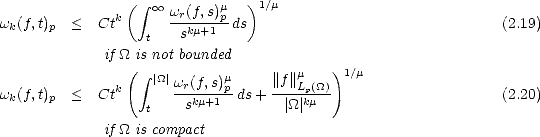
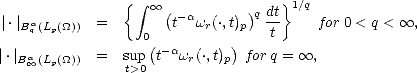
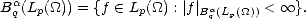
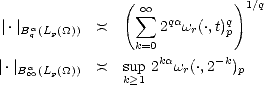
![( integral integral )1/p
wr(f,t;I)p = -1d |Drh(f,x)|pdxdh .
t [- t,t]d I(rh)](root200x.gif)
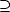
![r ( )
r sum r [ r r ]
D h(f,x) = k Dks(f,x+ kh)- D h+ks(f,x)
k=1](root201x.gif)
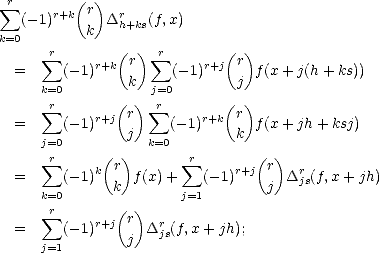
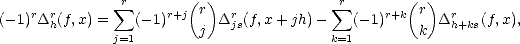
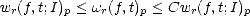
![integral
p -d r p p
wr(f,t;I)p = t [-t,t]d||D h(f,.)||Lp(I(rh))dh < wr(f,t)p](root205x.gif)
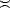
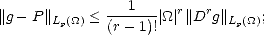
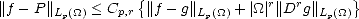
![[]](msam7-3.gif)
![||f- Tnf ||{Lp([]j,n) }
< Cp ||f- tj,n||Lp([]j,n) + ||tj,n - Qn(tj,n)||Lp([]j,n)
(use estimate 2.7 from Proposition 6 in page 53)
< C {E(f,TT(r);[] ) + E(t ,TT(r);I )}.
p,t j,n p j,n j,rp](root209x.gif)
![E(tj,n,TT(r);[]i,n)p
< ||tj,n- ti,n||Lp([]i,n)
< Cp {||tj,n- f||L ([] ) + ||f- ti,n||L ([] )}
p i,n p i,n
(use Lemma{ 2.4 in page 32) }
< Cp,|Ij,n| ,r ||tj,n- f||Lp(Ij,r) + ||f -ti,n||Lp(Ij,r)
< Cp,|Ij,n| ,n,tE(f,TT(r);Ij,r)p;](root210x.gif)
![||f- Tnf||Lp([] ) < Cp,|I | ,n,tE(f,TT(r);Ij,r)p,
j,n j,n](root211x.gif)
![p
||f - Tnf||Lp(_O_)
2 sum n- 1
= ||f - Tnf||pLp([]j,n)
j=1-r
(set l = max{lIj,r |1- r < j < 2n}
and c = 2nl)
2n-1
< C sum w (f,l ;I )p
p,c,n,tj=1-r r Ij,r j,rp
2n-1
sum p
< Cp,c,n,t wr(f,l;Ij,r)p.
j=1-r](root212x.gif)
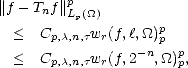
![-n
E(f,Xn)p < Cwr(f,2 )p. []](root214x.gif)
![( )
2n sum -1 || [n] ||p 1/p
C1||Sn ||Lp(_O_) < 2-nd|ak,r(Sn)| < C2||Sn||Lp(_O_).
k=1-r](root215x.gif)
||p|| N [n](x)|| p < C sum ||a[n](S )||px ;
n k (- /\ (x) k,r n k,r p,d,rk (- /\ (x) k,r n supp(N[kn],r)
n n](root216x.gif)
||p||supp(N[n])||< C 2-nd sum ||a[n](S )||p.
_O_ n p,d,r | k,r n || k,r| p,d,r k=1- r|k,r n|
k (- /\n(x)](root217x.gif)
![n n
- nd 2 sum -1 || [n] ||p -nd 2 sum -1 nd
2 |ak,r(Sn)| < 2 2 ||Sn||Lp(Jk,r),
k=1-r k=1-r](root218x.gif)
![( n )1/m
wr(f,2-n)p < C2 -nr ||f||m + sum [2krE(f,Xk)p]m ,
Lp(_O_) k=1](root219x.gif)
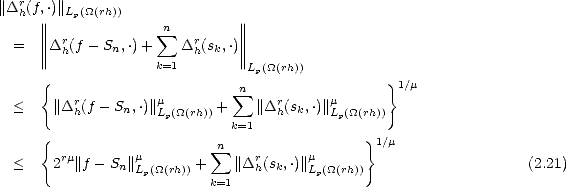
N [k],x ||
|| h j=1-r j,r j,r ||
|| k ||p
||2 sum -1 [k] r [k] ||
= || aj,r(sk)D h(Nj,r,x)||
j=1-r | | | |
< (2p-1)|/\k(x)|-1 sum ||a[k](sk)||p||Dr(N [k],x)||p (2.22)
----- ----- x (- /\k(x) j,r h j,r
Cp,d,r](root221x.gif)
![Drh(N [jk],r,x)
r [k]
= |h| | /_\ (N j,r(.);x,x+ h,...,x + rh)
= 1r!|h| rDrhN[jk,r](qx,r,h), (2.23)](root222x.gif)
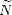
![[k]
DN j,r,x,h((t) )
= D N[0]o fk,j o fx,h (t)
0,|r
= DN [00],r|| .Dfk,j| f (t) .Dfx,h(t)
( fk,j(fx,h(t)) ) | x,h
@N[00,]r @N [00],r || k
= @x1--,...,-@xd- || .2 Idd .rh
| fk,j(fx,h(t))
sum d @N [00],r||
= 2kr hi-@x--||
i=1 i fk,j(fx,h(t))
= 2krDhN [0](x)
0,r](root224x.gif)
![|| ||
||DhN [jk,r]||L oo (_O_) < 2kr||||DhN 0[0,]r|||| < 2kCr
( )r-1|| L oo (_O_||)
||DrhN[jk,r]||L oo (_O_) < 2kr ||||DhN [00],r|||| < 2krCr
L oo (_O_)](root225x.gif)
![| |
||Drh(N [kj,]r,x)|| < Cr(2k| h|)r](root226x.gif)
![Drh(N [kj,]r,x)
( r-1 [k] )
= Dh D h (N j,r,x)
= D (--1--|h| r-1Dr- 1N [k](q ));
h (r-1)! h j,r x,r,h](root227x.gif)
![|| r [k] || || ( k(r- 1) r-1)|| k r-1
|Dh(N j,r,x)|< |Dh Cr2 |h| |< Cr(2 |h| ) .](root228x.gif)
![|| ||
||||Dr (N[k],.)|||| p
h j integral ,r Lp(_O_(rh))
|| r [k] ||p
= _O_(rh) /~\ supp(N[k])|D h(N j,r,x)| dx
integral j,r | |p
= ||Drh(Nj[k,r],x)|| dx
(G U G') /~\ supp(N[j|k,r]) | | |
< C {(2k|h| )rp||G /~\ supp(N[k])||+ (2k|h|)(r-1)p||G' /~\ supp(N[k])|| }
r j,r j,r](root229x.gif)
![|| [k]||
|supp(Nj,r)|](root230x.gif) =
= ![|||| r [k] ||||p
||D h(Nj,r,.)||Lp(_O_(rh))
{ }
< Cr 2krp2-kd| h|rp + 2kp(r-1)2-k(d-1)| h| (r-1)p|h|
kp(r- 1) -k(d- 1) kpr -kp -kd k
(notice that 2 kpr 2-kp -kd =kp2 2kpr 2-kd 2
{ < 2 2 2 2 = 2 2} )
< Cr 2krp2-kd| h|rp + 2kpr2-kd| h |p(r-1+1/p)
< Cr2kpc2-kd|h| pc,](root231x.gif)
![||Dch(sk,.)||Lp(_O_(rh))
( k )1/p
c kc 2 sum -1 -kd ||[k] ||p
< Cp,d,r| h| 2 2 |aj,r(sk)|
j=1-r
(use Lemma 2.20 above)
< Cp,d,r| h|c2kc|| sk||Lp(_O_(rh))](root232x.gif)
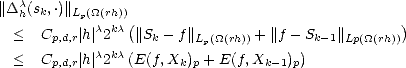
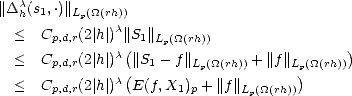
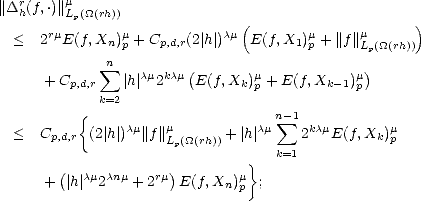
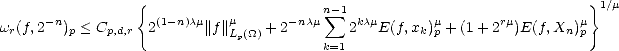
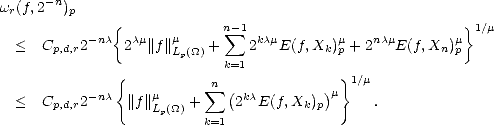
![( sum n [ ] )1/m
wr(f,2-n)p < Cp,d,r2-nc 2kcE(f,Xk)p m .
k=0](root238x.gif)
![( oo sum )1/q
N1(f) = [2naE(f,Xn)p]q
n=0
( oo sum [ ] )1/q
N2(f) = 2na||f- Tnf||Lp(_O_)q
n=0
( oo sum )1/q
N3(f) = [2na||tn(f)||Lp(_O_)]q
n=1](root239x.gif)

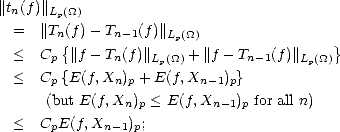
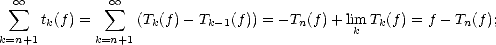
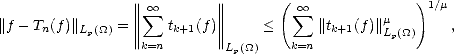
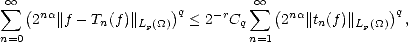
![Aaq(Lp(_O_),Xn) -~ Baq(Lp(_O_)) []](root244x.gif)
![n
sum oo sum oo 2 sum - 1 [n] [n]
f = tn(f) = aj,r(tn(f ))N j,r
n=1 n=1j=1-r](root245x.gif)
![( ) 1/p
{ sum oo 2n sum -1 | |p q/p}
N4(f) = 2anq || a[nj,]r(tn(f))|| 2-nd < oo .
n=1 j=1-r](root246x.gif)
![( oo sum )1/q
|a| laq(X) = [2na||fn||X]q ,
n=0](root247x.gif)
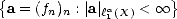
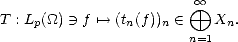

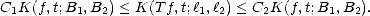

 <
<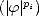


![E(g, Xn)p
( sum n sum o o )
= E ( sum k=1gk + k=n)+1gk,Xn p1
= E o o k=n+1gk,Xn p
|||| oo |||| 1
< |||| sum gk||||
||k=n+1 ||
( Lp1(_O_) )
sum oo m 1/m
< ||gk||Lp1(_O_)
k=n+1
( sum oo )1/m
< Cr,r,t ||a[n1]||mLp1(_O_) .
k=n+1](root253x.gif)
![oo sum na p1 oo sum ( na [1])p1
[2 E(g, Xn)] < Cr,r,t 2 an ;
n=1 n=1](root254x.gif)
![E(f - g,Xn)p2
= E( sum o o k=1tk(f )- sum o o k=1gk,Xn)p
( sum n sum o o 2 )
= E( sum k=1[tk(f)- gk]+ k=)n+1[tk(f)- gk],Xn p2
= E o o k=n+1[tk(f)- gk],Xn p
|||| oo |||| 2
< |||| sum [tk(f )- gk]||||
||k=n+1 ||
( Lp2(_O_) )
sum oo m 1/m
< ||tk(f)- gk||Lp2(_O_)
k=n+1
(notice that tk = Tk(tk(f )) = Qk(tk(f)) = tk(tk(f))
and gk = Tk(a[1]) = Qk(tk(f)))
( k )1/m
sum oo |||| ( [1])||||m
= ||Qk tk(f)- tk(ak ) ||Lp2(_O_)
(k=n+1 )
sum oo |||| ( [1])||||m 1/m
= ||(Qk o tk) tk(f)- ak ||Lp(_O_)
k=n+1 2
( sum oo |||| ||||m )1/m
< Cr,r,t ||tk(f)- a[1k]|| ;
k=n+1 Lp2(_O_)](root255x.gif)
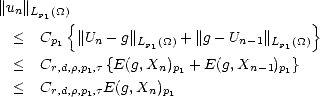
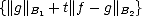 , and the statement follows.
, and the statement follows. 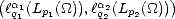

![( integral oo [ 1/p * ]q dt)1/q +
rp,q : M0(_O_, m) - ) f '--> t f (t) t- (- R (2.25)
0 ( integral oo [ ] )1/q
||.||L (_O_,m) : M0(_O_, m) - ) f '--> t1/pf**(t) q dt (- R+ (2.26)
p,q 0 t](root259x.gif)
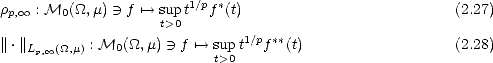
![||f||q
Lp,q integral (_O_,m)
= oo [t1/pf**(t)]q dt
0 t
integral oo [ integral t ]q dt
= t1/p-1 f *(s)ds -t
integral t= oo 0 s=[0 integral t ]q
= t-q(1-1/p) sf *(s)ds dt
t=0 s=0 s t
(use Hardy’s Theorem: estimate (1.5)
in page 8 for 1 < q < oo , and estimate
(1.9) i integral n oo page 12 for 0 < q < 1 )
< Cp,q t-q(1- 1/p)[tf*(t)]q dt
integral 0 t
oo [ 1/p * ]q dt
= Cp,q 0 t f (t) t](root261x.gif)
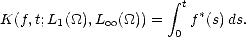
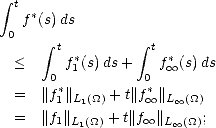
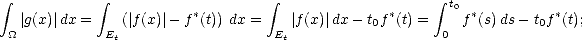
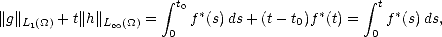
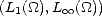
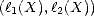
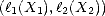
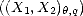
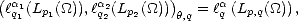
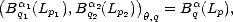


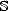
 = /\(.|f, h) : R -) x '--> f(h.x)x_O_d(x) (- R](root273x.gif)

 = f(h .x) = f(h.ch) = f (c).](root274x.gif)
| pdx = |f(h.x)| pdx < | f(h.x)|pdx = gd- 1 |f(t)| p dt,
_O_d _O_d Cyld(h) _O_1](root275x.gif)
![{f */\[g integral ,h]}(x)
= f(y)g(h .[x - y])dy
Rd
integral
= Rd f(y)g(h .[ch - y])dy
= {f * /\[g,h]}(ch);](root276x.gif)
|||Lq(_O_d) ||
|||| ||||
= || Rd f (x - y)/\[g,h](y)dy||L (_O_ )
integral q d
< |/\[g,h](y)|||f(.- y)||Lq(_O_d)
Rd integral
= ||f||L (_O_) | g(h.y)|dy
q d integral _O_d
< ||f||Lq(_O_d) Cyl (h)|g(h .y)| dy
d integral
= gd-1||f||Lq(_O_d) |g(t)| dt,
_O_1](root277x.gif)
![{ sum m }
Ym(F) = /\[fk,hk] : fk (- F,hk (- Pd- 1 .
k=1](root278x.gif)
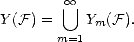

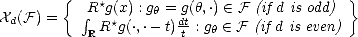
 0
0
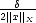
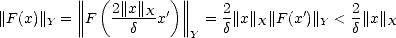



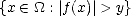
 inf
inf 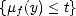

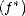
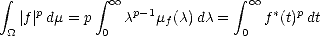
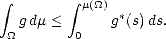
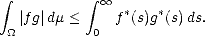
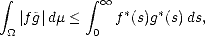
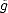
 1
1